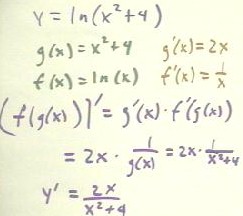
The first quiz problem was to find a derivative of y = ln(x^2 + 4), as shown below. Following standard procedure, using g(x) = x^2 + 4 and f(x) = ln(x) and noting that the derivative of ln(x) is 1/x, we calculate the derivative of the composite function as shown below.
The second quiz problem must find the derivative of e(ln x + 1) using the chain rule. We note that this function can be simplified using the laws of exponents to obtain e ^ ln x * e^1 = x * e^2 = e * x; since e is a constant number the derivative will simply be e * 1 = e.
Using the chain rule as specified, we use g(x) = ln x + 1 and f(x) = e^x to obtain derivative 1/x * e^(ln x + 1). This doesn't look much like e, which is the value of the derivative we found by simplifying the exponential function then taking the derivative. The pass to be the same. So we follow the same simplification idea as before, applying the laws of exponents as shown below. We see that the derivative we have obtained is indeed equal to just e.
The derivative of arcsin(x)
We now find the derivative of the function g(x) = arcsin(x). Its inverse function is f(x) = sin(x), and as usual the composite function f(g(x)) = x with derivative 1. The chain rule tells us that the derivative is also equal to g'(x) * cos(arcsin(x)). When this expression is set equal to 1, the other expression for the derivative, we will obtain an equation we can solve for g'(x). That is, provided we can find an expression for cos(arcsin(x)).
As we will see below, cos(arcsin(x)) = `sqrt(1-x^2). Using this result we obtain g'(x) * `sqrt(1-x^2) = 1, so g'(x) = 1 / `sqrt(1-x^2).
To see why cos(arcsin(x)) = 1 / `sqrt(1-x^2), we first observe that arcsin (x) is the angle whose sine is x. That is, on a unit circle with origin at the center, arcsin(x) is the angle whose y coordinate is x. This might seem a bit weird, but we are simply following the definition of the sine function, which says that the sine of an angle is its y coordinate when that angle is plotted in the usual manner on a unit circle. If, as implied by the expression arcsin(x), we are looking for an angle whose sine is x, then the corresponding y coordinate must be x. This relationship is pictured in the figure below.
We see that arcsin(x) is the angle corresponding to a hypotenuse of 1 and a vertical side of x. The cosine of this angle it is the corresponding x coordinate. By the Pythagorean Theorem this x coordinate is `sqrt(1 - x^2). We therefore see that cos(arcsin(x)) = `sqrt(1-x^2), as claimed above.
A text problem stated that the force exerted by a rocket moving away from the Earth was given by F = k / r^2, where r is the distance of the rocket from the center of the Earth. If the rocket is moving away from the center of the Earth at .2 km / sec, then at what rate is the force changing with respect to time?
We first note that on Friday we determined that the work done in moving from distance r1 to r2 from the center of the Earth is the integral of F(r) dr; in this case F(r) = k / r^2, so the work done is the integral shown below. This is not relevant to the stated problem, except to put it in the context of work we have done before.
To find the rate which force is changing with respect to time, we find the derivative dF / dt. Sense F is a function of r, which is in turn a function of t, we will use the chain rule in the form dF / dt = dF / dr * dr / dt. The quantity dr / dt is the rate of which r is changing with respect to time, which is simply the .2 km / sec rate given above. The quantity dF / dr is easily found by taking the derivative of F = k / r^2; we obtain dF / dr = - 2 k / r^3. The result is that dF / dt = -2 k / r^3 * (.2 km / s) = 0.4 km / s * k / r^3. If we know k, then this allows us to find dF / dt for any distance r.
As another application of the chain rule, suppose that the speed of a ship accelerating out of a harbor is v = .003 t^2, and that the force necessary to accelerate the ship is F = 24,000 v^2, with the speed given in meters/second when t is in minutes, and F in Newtons of force when v is in meters/second. (Note that the velocity here is increasing at an increasing rate, which is not very realistic; a ship might attempt to maintain a uniform acceleration, with v = c * t for some constant acceleration c, but usually the velocity actually increases at a decreasing rate).
We wish to find the rate which the force F changes with respect to time. We therefore find dF / dt. Since F is given as a function of v and v is given as a function of t, we use the chain rule in form dF / dt = dF / dv * dv / dt and we obtain dF / dt = 48,000 v * (.006 t). Substituting v = .003 t^2, we obtain dF / dt = .864 t^3, as shown below.
The power that the ship must provide is given by P = F * v. We might wish to find the rate at which the required power changes. This rate would be (dP / dt). Since P = F * v, we have by the product rule P' = (F * v) ' = F' v + F v', where all derivatives are with respect to t. Using the expressions for F' and v' found above, it is not difficult to find that dP / dt = .864(.003) t^5 + 24,000 (.003 t^2) ^2 * (.006 t), which simplifies to a single multiple of t^5. The power therefore increases as the fifth power of t, which means that it gets out of hand rather quickly. This is why ships don't usually accelerate at increasing rates, at least not on a sustained basis.
Implicit Differentiation
If we assume that y is a function y(x) of x, and if we suppose that for some reason x y + y^2 = 8, then we could solve this equation for y and determine the derivative y' = dy / dx. Solving the equation for y would not be too difficult, though it would probably involve the quadratic formula, and taking the derivative of the resulting solution would be a bit tedious but moderately easy.
If, however, we are interested in obtaining the derivative y' only as a function of y and x, we can use the process called implicit differentiation. Note that whether or not we actually solve for y, it is implicit in the equation xy + y^2 = 8 that there is some function y(x) that solves the equation. This is true even if we don't know how to solve the equation, even if the equation is mathematically impossible to solve in the usual sense.
To differentiate the function implicitly, we simply take the derivative of both sides of the equation with respect to x. The derivative of the first term, xy, is just x' y + x y'; we know that x' is 1 (and perhaps should have written it this way in the fourth line), though we don't know what the derivative y' is because it represents the derivative of a function y(x) for which we don't have a formula.
The derivative of y^2 is (y^2) '. Since y itself is a function of x, we can't follow temptation and say that (y^2) ' = 2y. We must instead treat y^2 as a composite of the function y(x) and the squaring function. We see therefore that by the chain rule we must include the derivative y' of y, obtaining (y ^ 2) ' = y' * 2y. We write this below as 2 y y'.
In the fifth line of the figure below we isolate all the terms containing y' on the left-hand side, then in the next step we factor out the y' (and belatedly note that x' is 1) and in the final step we divide both sides by the coefficient of y' to obtain y' = -y / (x + 2y). This allows us to determine y' anytime we have values for x and y.
In the figure below we look more closely at the reason that (y^2)' = 2 y y'. If we write the expression as (y(x)) ^ 2, explicitly showing the dependence of y on x, then proceed to use the f(g(x)) notation we see that g(x), the first function to act on x, is just y(x), while f(x) is the squaring function f(x) = x^2. For these functions, f(g(x)) = (y(x)) ^ 2. It follows that (y^2)' = f(g(x))' = g'(x) * f'(g(x)) = g'(x) * 2 g(x) = y'(x) * 2 y(x) = 2 y y'.
Below we work out the same problem using the d / dx notation instead of the ' notation for the derivative.
We can also use the d / dx notation to understand why d / dx (y^2) = 2 y * dy / dx. If we let f(x) be y, and use df / dx = df / dx = df / dy * dy / dx, the result follows immediately as shown below.
As an application we consider the equation x^2 y + y^2 x = 16. Whatever the explicit form of the implicit function y(x), we know that the graph of y vs. x must contain the point (2,2), since x = 2 and y = 2 satisfies the equation. If for example we wished to find the equation of the tangent line to the graph at this point, we would need only to find the slope that this point. We can find a slope by the process of implicit differentiation.
Differentiating both sides of the equation implicitly, we obtain the equation shown below. Solving this equation for y' we obtain y' = (-2x - y^2) / (x^2 + 2 xy); this expression, being the value of y' = dy / dx, will give us the slope of the graph at any graph point. Evaluating y' at the point (2,2), we obtain slope y'(2,2) = -2/3, as shown below.
We could easily proceed to find the equation of the tangent line; the slope = slope form is ( y - 2) / (x - 2) = -2/3. Whenever the function, this tangent line will provide an approximation near the point (2,2) of the graph of y vs. x.
"