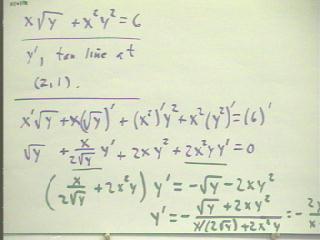
The quiz problem for today was to find y' for the implicit function defined by x `sqrt(y) + x^2 y^2 = 6 and to determine the equation of the tangent line to the graph of this function at the point (2,1). We were then to find the approximate value of y when x = 2, using the tangent line approximation, and to plug the coordinate so the resulting point into the defining equation to see how close the resulting statement was to equality.
We begin as usual by implicitly differentiating both sides of the equation. Using the product rule on each of the terms on the left-hand side we obtain x' `sqrt(y) + y `sqrt(y') for the derivative of x `sqrt(y), and we obtain (x^2)' + x^2 (y^2)' for the derivative of x^2 y^2; the resulting derivative give us the equation `sqrt(y) + x / (2 `sqrt(y)) y' + 2 x y^2 + 2 x^2 y y' = 0. We use the usual methods to obtain y' = -(`sqrt(y) + 2 x y^2) / ( x / (2 `sqrt(y)) + 2 x^2 y); since this expression contains a fraction in its denominator we can simplify it by multiplying both numerator and denominator by 2 `sqrt(y); we obtain y' = - ( 2 y + 2 x y^(5/2)) / (x + 2 x y^(3/2)).
The algebra would have been simpler had we multiplied everything in the equation by 2 `sqrt(y) as soon as this expression appeared as a denominator (i.e., just after completing the implicit differentiation). This would have given us and equation without any fractions, which is generally a desirable state. In the figure below we show the resulting algebra. Note that we obtain the same expression for y' as before, with fewer and more easily understood steps.
We evaluate our expression for y' at (2,1). At (2,1) we obtain by a simple substitution into the expression for y' the value y' = -5/9. You should verify this.
We now have the point (2,1) and the slope -5/9 of the line tangent to the graph of the implicit function. Using the usual procedure we construct the equation of the straight line through this point, obtaining y = -5/9 x + 19/9.
Using this tangent line approximation we find the approximate value of y at x = 2.2. Since our equation has fractional coefficients, we note that 2.2 is equal to 22/10, which reduces to 11/5. Substituting this value into the equation we obtain y = 8/9.
Substituting this value into the original defining equation, we obtain the approximate value 5.9 for the left eye on hand side. So our equation becomes the statement 5.9 = 6, which is not quite true but is pretty close. This indicates that the point (2.2, 8/9), or more consistently (11/5,8/9), is pretty close to the graph of the implicit function.
An approximate graph of this situation is depicted below. We note that four points on the tangent line, as long as x is near 2, it is nearly true that x `sqrt(y) + x^2 y^2 = 6.
You should make a DERIVE plot of this situation. Simply author the defining equation x `sqrt(y) + x^2 y^2 = 6 and plot it with appropriate x and y ranges. Your window should contain the point (2, 1). If you then author the equation y = -5/9 x + 19/9 of the tangent line, you will see that the line is indeed tangent to the graph at (2,1). By narrowing the window in the vicinity of (2,1), or by zooming in on this point, you can see how the difference between the tangent line and the graph of the function practically disappears as we get closer closer to (2,1).
L'Hopital's Rule
L'Hopital's Rule can be understood in terms of the figures below. In the first figure we see two functions f(x) and g(x), both of whose graphs approach the point (a,0). We wish to find the limit of the quantity f(x) / g(x) has x -> a, but we cannot simply calculate f(a) / g(a), because this quantity approaches zero.
We do note, however, that each function has a local linearization near the point (a,0). The local linearizations have been indicated by the straight line segments converging at the point (a,0). The segments have slopes f'(a) and g'(a).
In the second graph in the figure below we consider the effective moving a distance `dx from the point (a,0). From the corresponding point on the x axis, we can get to the point on the graphs of the local linearizations by moving vertical distances f'(x) `dx to the local linearization of f(x), and g'(x) `dx to the local linearization of g(x). (Each of these quantities can be understood by constructing the appropriate slope triangle from the point (a,0), with a run of `dx; the rise in each case will equal the product of the slope and the run; since the slopes are f'(x) and g'(x) the rises are f'(x) `dx and g'(x) `dx).
In each case, since the y coordinate of (a,0) is zero, the y coordinate of the local linearization will be equal to the vertical rise. The y coordinate of the local linearization's will therefore be f'(x) `dx and g'(x) `dx. Since as we approach (a,0) the values of f(x) and g(x) approach those of the local linearization, when we are near x = a we thus have, to an increasingly good approximation, f(x) / g(x) = f'(x) `dx / [ g'(x) `dx ] = f'(x) / g'(x).
We can also understand l'Hopital's Rule from the equations of the tangent lines. It should be clear that these equations are(y - 0) / (x - a) = f'(a) and (y-0) / (x-a) = g'(a), which when solve for y give us y = f'(a) * (x-a) and y = g'(a) (x-a); the ratio f(x) / g(x) will therefore be near the ratio f'(a) (x-a) / [ g'(a) (x-a) ] = f'(a) / g'(a) of the local linearizations whenever x is near a.
We wish to use l'Hopital's Rule to determine which of the functions y = ln(4x+7) and y = x^.01 dominates as x -> infinity. Since for any positive value of y we can solve either function for x, there will be an x value corresponding to any y value, no matter how large. It follows that both functions have infinite limit at infinity. We can therefore apply l'Hopital's Rule to the ratio ln(4x+7) / x^.01. If we find that the limit is infinite, this will mean that the natural log function dominates; if the limit is 0 then the power function dominates; and if the limit is finite but not 0, neither function will dominate.
The application of the rule is straightforward. We calculate the ratio of the derivatives 4 / (4x+7) and .01 x^-.99. In the third line below we expressed the fraction in terms of positive exponents. At this stage we might note that since the numerator is a power function with exponent .99 and the denominator for large values of x is dominated by the power function x^1, the denominator has a larger exponent and therefore dominates so that the limit will be zero. To be sure of this, we divide both numerator and denominator by x^.99 to obtain the fraction 1 / (4 x^.01 + 7 x^-.99). It is clear that the first term of the denominator, with its positive power of x, approaches infinity as x approaches infinity and that the second term of the denominator, with its negative power of x, approaches 0; the result is that the denominator approaches infinity so the whole fraction approaches zero.
From this we conclude that the denominator function x^.01 of the original expression dominates the natural log function.
Relative Maxima and Minima
A local maximum of the function occurs at any point x = xM where the value of the function is greater than its value in at least some small neighborhood of that point.
If the function behaves itself well enough so that it has a derivative in some neighborhood of x = xM, then it should be clear that the derivative of the function must be zero at x = xM; if the derivative wasn't zero, then the graph of the function would have a nonzero at x = xM, and hence would be greater either to the right or to the left of x = xM (to the right if the derivatives positive and to the left is the derivative is negative). In that case x = xM could not be the local maximum.
Unless the function is linear in the neighborhood of x = xM, it also follows that the derivative to the left of a maximum point is positive, since the function is increasing up to this point, and that the derivative is similarly negative to the right of the maximum point. Therefore the maximum point has the characteristic that the derivative function f'(x) changes from positive to negative at x = xM.
The figure below summarizes these ideas.
It should be clear that everything that has been said about a local maximum can be adapted to the case of a local minimum
As an example, consider the function y = f(x) = x^2 + 2x - 5. We wish to determine whether there is a local maximum or minimum for this function.
Following the ideas presented above, we begin by looking for a point where the derivative is 0; at such a point the function 'levels off', and a point with this characteristic is a good candidate for a relative maximum or minimum. An x value with the characteristic that the derivative 0 for that value of x is called a critical point for the function.
The derivative of the function f(x) given above is easily found to be f'(x) = 2x + 2; this derivative is 0 when x = -1. Thus we have a critical point at x = -1.
To determine whether this point is a maximum or a minimum, we look at the behavior of the derivative when x < -1 and when x > -1. If the derivative goes from positive to negative, this means that the function must have a maximum at this point. If only other hand the derivative goes from negative to positive, we will conclude that the function is decreasing to the left of the critical point and increasing to the right of the critical point, and our critical point will therefore be a local minimum.
If x < -1, the derivative 2x + 2 will clearly be < 0. In fact, if we solve the inequality 2x + 2 < 0, we easily obtain the inequality x < -1.
Since the inequality 2x + 2 > 0 has solution x > -1, we conclude that the derivative is positive to the right of the critical point.
Since the derivative is negative to the left of the critical point and positive to the right, we conclude that the critical point x = -1 is a relative minimum for the function.
These ideas are presented graphically in the figure below, which is accompanied by a possible sketch of the function. The figure shows that the derivative is 0 at x = -1, negative for x < -1 and positive for x > -1.
We can locate the coordinates of the minimum point by substituting x = -1 into the formula for the function. We obtain f(-1) = -6 (you should validate this possibly incorrect calculation), and we conclude that the minimum occurs at the graph point (-1, -6).
The figure below shows how the decreasing derivative implies that the second derivative is negative. The chords of the graph have slopes equal to the average values of the derivative function; it is clear that the slopes begin positive then as we move to the right approach 0; as we pass the local maximum the slopes become negative. So we say that the derivative function f'(x) is clearly decreasing.
Since the second derivative gives the rate at which the derivative changes, and since the derivative is decreasing, it is clear that the second derivative must therefore be negative in the vicinity of this local maximum.
We therefore see that if the second derivative is negative at a critical point, that critical point must give us a local maximum. This statement, and the related statement that a positive second derivative at a critical point implies a local minimum, constitutes the second derivative test.
For many functions there are places where the graph is concave downward and other places where it is concave upward. A point where the concavity changes from downward to upward is called a point of inflection. On one side of a point of inflection, the function is concave downward so the second derivative is negative; on the other side of the point of inflection the function is concave upward and the second derivative is therefore positive.
We can therefore find a point of inflection by finding the regions where the second derivative is negative and where is positive.
"