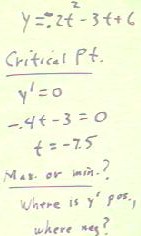
The quiz problem for today was to find the points at which the function y = -.2 t ^ 2 - 3 t + 6 has relative maxima and/or minima, using both the first and second derivative tests.
We begin by finding the critical point(s) for the function. We see that y' = -.4 t - 3, so that y' = 0 when t = -7.5.
We need to determine whether this critical point is a maximum or a minimum (or perhaps a point of inflection).
To use the first derivative test, we need to determine whether y' goes from negative to positive or from positive to negative at the critical point.
To do this we determine where the derivative is positive and where it is negative. As shown below, we see that y' < 0 when t > -7.5, and y' < 0 when t < -7.5.
We therefore conclude that at the critical point t = -7.5, the derivative on the left (where t < -7.5) is negative while the derivative on the right (where t > -7.5) is positive. Our conclusion is that the point is a maximum.
We summarize the first derivative test in the figure below. Whenever the derivative function is zero we have a critical point. At a critical point, if y' goes from positive to negative the point is a relative maximum while if y' goes from negative to positive the point is a relative minimum. To determine where y' is positive where it is negative, we can construct an accurate graph of y'; this graph will show us the zeros of y' and will therefore also shows where y' changes from positive to negative or negative to positive. We can also choose to solve the equations y' < 0 and y'>0, which will show us the regions where the derivative is positive and negative.
To apply the second derivative test to the same function, we again find critical point t = -7.5. We then find a second derivative, which as you can easily verified is y'' = -.4. With us see that the second derivative is always negative, so the graph is always concave downward. The derivative is decreasing (if the figure below shows that the derivative is increasing, the figure is incorrect), so the critical point necessarily gives us a maximum.
In the figure below we depict the shape of a container into which water is flowing a constant rate. We wish to sketch and approximate graph of depth y vs. clock time t.
It should be obvious that the water depth will be changing most rapidly where the container has its minimum width. The slope of the depth vs. clock time graph, as you should know very well, represents the rate at which water depth is changing, so that the faster the water depth changes the steeper the graph will be. Thus our graph of depth vs. clock time will get steeper and steeper as y approaches is point of minimum width, then will become less and less steep as the width becomes greater.
While the graph is getting steeper and steeper, the derivative of the depth function is increasing and the concavity of the graph will be upward; y'' will be positive. While the graph is getting less and less steep, the derivative of the depth function is decreasing and the concavity of the graph will be downward; y'' will be negative. The point at which the concavity changes will be a point of inflection, and will coincide with the depth y at which the container's width is a minimum.
Families of Functions
Families of functions can tell us a great deal about the behavior of things that we can observe in the real world. One example is that of vertical motion under the influence of gravity. If a ball is tossed into the air in the vertical direction at height y0 with velocity v0, physics tells us that the height vs. clock time function will be y = -4.9 t^2 + v0 t and y0, where y is in meters when t is in seconds, v0 is in meters/second and y0 is in meters.
It is clear that the vertical position of the object at clock time t depends completely on its initial velocity v0 and initial height y0. Since many different initial velocities and initial heights are possible, we can understand the height vs. clock time behavior of such objects by looking at what happens when v0 and y0 are varied.
We look at graphs of possible y vs. t functions, corresponding to various values of y0 and v0.
It should be clear that a graph of the function y vs. t will be a parabola, since the function is quadratic.
y0 is the initial altitude, and will therefore be represented by the y intercept of the graph of y vs. t.
Since velocity is the derivative of the position function, we see that the initial velocity is the slope of the function at the y intercept y = y0.
Since the coefficient -4.9 of t^2 is constant, although parabolas will have the same shape. To obtain the graph of y vs. t for a given initial position and velocity, we need only moved this fixed shape around until its slope that y = y0 is equal to v0. Thus, for the three different initial velocities indicated by the red slope lines at y = y0, we obtain the three graphs shown in the figure below.
NOTE: DERIVE file on above clip: d:\fall98\cal_1114 (same path, etc., 1113 also relevant)/ Distance students: request this file by name if you don't have it and it will be E-mailed.
We can interpret the graphs as follows. If an object is released at altitude y0 with a large positive velocity v0, corresponding to being thrown upward at a large velocity, it will rise higher, as indicated by the greater y value of the maximum on the graph corresponding to larger positive v0 (and matching the greater of the positive initial slopes v0). The object will also spend more time rising to its maximum altitude, corresponding to the greater value of t at the critical point, and will remain in the air longer, corresponding to the greater value of t when the object reaches y = 0 (generally assumed to correspond to the altitude of the floor or the ground from which altitude is measured).
If the initial velocity of the object is still positive but smaller (corresponding to the object being thrown upward, but not as fast as before), the parabola must move over and down in order to match the correspondingly smaller initial slope v0; we see that the object takes less time to reach its maximum altitude, as expected, and as expected stays in the air for less time.
If the initial velocity of the object is negative, corresponding to an object being thrown downward from altitude y0, the parabola must be moved to the left and upward in order to match the initial slope, and we get a graph which for positive values of t has no relative maximum (the relative maximum of the parabola was shifted to the left of the y axis and has nothing to do with the motion of the object), and which reaches y = 0 more quickly than for any case where the initial velocities positive (corresponding to the object being thrown upward).
Another important function family models the shape of a standing wave at an instant. Your text implies that the model we are about to obtain is a model of a wave, and this is not so. A model of a wave involves both its shape in space and its motion and time, and is a function of two variables which can be represented by x and t. The model we show here has no t dependence, since it comprises merely a snapshot of a certain type of wave at an instant. You can think of a guitar string, fixed at both ends and vibrating as a pure sine wave (the vibration of a real guitar string will not be so pure, but as a simplification we can still think of it as if it was).
We know that the graph of a function y = A sin (bx) undergoes a complete cycle when bx changes by 2 `pi, which happens when x changes by 2 `pi / b. The text calls this the period of the wave; this is consistent with the mathematical meaning of the period of a sine function, but when we talk about the actual distance between the peaks of a sine wave, we call this distance the wavelength. The period of a sine wave is the time interval between the passage of successive peaks.
The parameter A, as we will know, gives the maximum distance of the graph from the x axis, and corresponds to the maximum displacement of the vibrating object from its natural stationary position (called the equilibrium position).
The figure below should clarify the effects of changing A or b. Recall that bx will correspond to the angular position of a point on the reference circle, and that when bx has moved through one revolution, the function will have completed one cycle; this again is why the wavelength is 2 `pi / b. If b is large, it will take as much change in x to drive the reference circle point around the circle, and the wavelength will be correspondingly small. Conversely if b is small, they will take a greater change in x to complete the cycle and the wavelength will be correspondingly large. Smaller and larger wavelength are indicated and labeled in red on the graph that the bottom of the figure below.
If A this small, the amplitude will be correspondingly small, as indicated by the black curve.
Another important class of functions, essential in the study of statistics, is the family e ^ -[(x-a)^2].
In the figure below we sketch a table for the a = 0 function e ^ -(x^2). We see that the function is symmetric about x = 0, for the obvious reason that x is squared in gives the same results for positive as for negative x values of the same magnitude. At x = 0, the value the function is clearly 1; and x = -1 and -2, the function values are e^-1 = .37 and e^-4 = .01 (you should validate these possibly incorrect approximate values). The corresponding graph is shown in blue in the figure below.
A table for e^ -[(x-a)^2] is shown below. When x = a, we see that x-a will be zero so that the function will take value e^0 = 1. When x = a-1 or a+1, (x-a)^2 = 1 and we see that corresponding values of the function will be e^-1; we see similarly that for x = a -2 or x = a + 2, we must obtain values e^-4 = .01. The table has the same y values as that for e^-x^2, but with the x values shifted to the right a units. The graphs of e^ -[(x-a)^2] will therefore be identical to those of the graph of e^-x^2, but will be shifted either to the right (for positive values of a) or to the left (for negative values of a). Two such graphs are shown in the figure below.
The family of functions e^-(x^2/b), for b > 0, is also a great importance and applications. The b = 2 function e^-(x^2 / 2) is the basic 'bell-curve' function used in statistics.
All the functions of this family have their maxima at x = 0, as can be seen from the fact that e^0 = 1 and e^-(x^2 / 2) = 1 / e^(x^2 / 2) must always been less than 1.
Greater values of b will cause the exponent -x^2 / b to decrease through negative values less quickly, so that the function values will decrease towrad zero more gradually, while smaller values of b will permit the exponent to decrease through negative values more quickly and will result in a function which decreases more quickly.
The figure below depicts the behavior of this family.
"