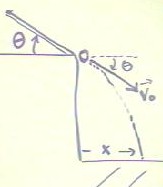
We begin by observing a ball rolling down and incline of fixed length. The ball rolls off the end of the incline, which is positioned at the edge of a table, and falls to the floor. We observe that when the other and is raised slightly above the table, the ball will roll down the ramp and off the end at the edge of the table, that it will fall to the floor. The parabolic path it follows to the floor will end when the ball strikes the floor at some distance x from the point directly below the edge of the table.
Now when the far end of the incline is raised a bit more, the ball again rolls down the incline, off the edge in strikes the floor. This time, since it gained more speed on the steeper incline, the ball travels further in the horizontal direction before striking the floor. This continues as we continue to raise the incline; but it is clear that can't continue forever, since the incline will eventually be vertical and this will result in the ball striking the floor directly below the edge of the incline, with no horizontal distance.
So we see that two influences, one the speed of the ball and the other the angle at which the ball leaves the end of the ramp, combine to determine the horizontal distance traveled after leaving the ramp. As the incline increases, the speed of the ball increases, tending to increase the horizontal distance. On the other hand, the angle of the ball's initial motion upon leaving the ramp gets closer and closer to vertical, tending to decrease the horizontal distance. It seems reasonable to conjecture that at some angle, the latter influence will overcome the former, and the ball will reach a maximum horizontal range.
The basic situation is depicted in the figure below. The ball will leave the end of the ramp at some angle `theta and some initial velocity v0. It will travel a horizontal distance x after leaving the ramp.
Actual observations of a ball rolling down a ramp of length 63 cm and falling a distance of 96 cm to the floor seems to indicate that the ball travels farthest in the horizontal direction when the raised end of the ramp is held at an altitude of between 33 and 37 cm above the tabletop.
We wish to find some function that models the horizontal distance x, and to maximize this function to validate and explain our observations. Our model and our explanation will involve some results from physics. These results will simply be quoted; any explanation of the physics will be parenthetical and may be ignored by anyone not interested in these details.
Direct observation also showed us that the time of fall for a dense object seemed to be independent of the size or mass of the object, or of its horizontal velocity.
Simple trigonometry shows that we can resolve the velocity v0 into components parallel to a horizontal x axis and to a vertical y axis. In the figure below we see that these components will be -v0 sin(`theta) and v0 cos(`theta).
It is more convenient to measure the height to which the raised end of the ramp is elevated then to attempt to measure the angle directly, as with a protractor. If the length of the ramp is L and the height of the raised end is h, then by the definition of the sige function we see that sin(`theta) = h / L.
From the fact that for any angle `theta, sin^2(`theta) + cos^2(`theta) = 1, we can see that cos(`theta) = `sqrt(1 - sin^2(`theta)). Substituting h/L for sin(`theta) and simplifying this expression as below we see that cos(`theta) = `sqrt( (L^2 - h^2) / L^2) = `sqrt(L^2 - h^2) / L.
We now see that the vertical and horizontal complements of the initial velocity in the y and x directions are v0y = - v0 sin(`theta) = - v0 (h / L) and v0x = v0 cos(`theta) = v0 `sqrt(L^2 - h^2) / L.
Physics tells us that, in this situation, v0 = `sqrt(1400 h). (For anyone interested in the physics, note that we obtain this by setting 5/7 of the total decrease mgh in potential energy equal to the kinetic energy .5 m v0^2 attained when the ball is released from rest. We then solve for v0. The 5/7 comes from the assumption that the ball rolls without slipping, and that therefore 2/7 of the potential energy decrease will go into rotational kinetic energy of the ball and will not contribute to the translational velocity of the ball.)
Using this expression for v0, we see that the initial y velocity is v0y = -`sqrt(1400 h) (h/2), which simplifies to -`sqrt(1400)/L * h^(3/2). (Note that instead of v0y and v0x in the figure below, these initial and final x and y velocities have simply been labeled vy and vx; it should have been done otherwise). The initial x velocity is v0x = `sqrt(1400) / L * `sqrt(L^2 h - h^3).
Our strategy for obtaining and expression for the horizontal distance x will now become clear. We will solve the expression for the altitude y as a function of clock time t for the time when y = 0, which is when the ball will hit the floor. We will then use this time and the initial x velocity, noting that since gravity only pulls downward the x velocity will not change as the ball falls, to easily find and expression for how far the ball travels in the horizontal direction during the time of fall.
Recall the equation y = -4.9 t^2 + v0 y t + y0 used as an example in your text section on function families. This equation models the altitude of an object falling freely under the acceleration of gravity, where altitude y is in meters when clock time t is in seconds. Since we are here working in units of cm and seconds, we instead use y = -490 t^2 + v0 t + y0. (Physics students will recognize this as the equation `ds = v0 `dt + .5 a `dt^2, where `ds is the displacement y - y0; the 490 represents 1/2 a, where a is the acceleration 980 cm/s^2 of gravity; in the original equation the acceleration of gravity was expressed in m/s^2).
We use this equation with v0y = - `sqrt(1400) / L * h^(3/2), the expression for v0y found earlier. We also agreed to measure the altitude of the ball from the floor, so the altitude at time t = 0 is y0 = 96 cm. We thus obtain the equation in the fourth line of the figure below.
We now wish to know when the ball hits the floor. The first answer to this question is simple enough: the ball hits the floor when y = 0. So we can set y equal to 0 and solve the equation for the time t required to fall.
Using the quadratic formula we obtain the solutions shown below. Noting that only the positive value of time t has relevance in this situation, we use only the positive solution. Since the denominator is negative, we must use a negative numerator. Since h and L are both positive numbers, the first term of the numerator is positive, which is a bad start when we are looking for a negative numerator but we have to accept it and see if the second term might not give us a negative. We note that if we had only the first term under the radical, the square root would be equal to the first term of the numerator and the numerator would therefore be zero. We are, however, adding 190,000 to the first term under the radical; this makes the square root larger in magnitude then the first term of the numerator and hence insures us that if we use the - of the +-we will obtain a negative numerator.
We therefore see that we must have t = { `sqrt(1400) / L * h^(3/2) - sqrt[ 1400 h^3 / l^2 + 190,000 ] / -980. (Note that the 190,000 is an approximation; you can and should obtain the accurate value for this number and keep it in mind throughout the rest of the solution).
It might not seem like it, with all the messy algebra involved here, but it is now easy to find an expression for the horizontal distance x. We have an expression for the time t required to fall, and we have an expression for the unchanging x velocity. We know that the find distance we multiply velocity by time (e.g., 60 mph for four hours implies a distance of 240 miles).
In the figure below we reiterate the expressions for the time t of fall and the initial x velocity v0x. We obtain and expression for the distance, as shown below (part of the last radical is cut off; you should recognize the expression here as our friend `sqrt(1400/L^2 + 190,000) ).
This expression for distance has only one variable, which is the altitude h of the raised end of the incline above the table. The other symbol in this expression is L, which just stands for the length of the incline and is not variable.
Since this expression is thus a function of the single variable h, we designate it x(h).
This function x(h) represents the horizontal distance traveled by the ball, which is the function we wish to maximize.
We can somewhat simplify the expression for x(h) by letting k stand for `sqrt(1400) / L. For any incline L will be a fixed number, so k will just be a constant that depends on the specific incline used.
We make this substitution and obtain the expression shown below.
Recall that we are trying to find a maximum for the function x(h). We will thus proceed to find critical points, and use a first- or second-derivative test to determine whether we have a maximum or a minimum.
Since we will wish to take the derivative of x(h) with respect to the variable h, we will use the distributive law to break the expression into two expressions, both of which are simple composite functions for which derivatives are fairly easy to compute. Noting that `sqrt(L^2 h - h^3) * h^(3/2) = `sqrt(L^2 h - h^3) * `sqrt(h^3) = `sqrt(L^2 h^4 - h^6), we obtain the first term in the second line below. The second term nearly combines the two square roots obtained from the distributive law; the two binomials under this radical are multiplied to obtain the expression in the third line.
We note that we now have to terms, each of which is of the form constant * `sqrt(polynomial in h). It will be easy to take these derivatives.
Writing each term as c f(g(h)), with g(h) being the polynomial under the radical and f(x) = `sqrt(x), we easily take the derivatives, obtaining the expression below for x'(h).
At this point the algebra becomes somewhat daunting. As a matter of fact, it is very likely that the algebra becomes impossible because we already have an expression involving polynomials of degree 5, and by the time we are done getting rid of our radicals we will probably end up with a polynomial whose degree is in the teens. Since we can't reasonably expect to find exact roots for any polynomial of degree more than 5, we are probably out of luck if we want and exact solution.
We can, however, use a computer algebra system to plot our function x'(h) vs. h, and we can then determine with any accuracy we desire the location of the zeros of this function. We can also see that this derivative function passes through its single zero by changing from positive to negative, indicating by the first derivative test that the critical point is giving us a maximum.
What we expect for our specific ramp, whose length is 63 cm and for which the maximum distance x occurred when h was equal to 36 cm, is that our function x(h) will be zero when h = 0 (the ball will have 0 horizontal range if the ramp isn't inclined at all) and also when h = 63, which would correspond to a vertical incline. The functional then wreak a peak around h = 36. The graph below shows this behavior.
So we expect our x'(h) function to be positive up to h = 36 or so, then 0 at the maximizing h, then to be negative for greater h values.
As another example of optimization, we maximize the function M(x) which gives the bending moment of a beam whose weight is w and length is L. In contrast with the preceding example, where the idea was simple but the algebra was very complicated, it is very straightforward to maximize this function. We began by finding the derivative dM / dx, as shown below, and find the critical point x = L/2. Noting that the second derivative is always negative, we see that the graph is always concave downward and any critical point must therefore give us a maximum. We conclude then that the beam experiences its maximum bending moment halfway along its length.
The figure below depicts an individual pulling a sled by means of a rope inclined at angle `theta above horizontal. Because of friction and other factors, the force required to pull the sled depends on the angle `theta. For large angles `theta, the upward component of the force will tend to decrease the frictional resistance; however, the larger the angle the smaller the component of the force in the direction of motion. We thus have two contrasting influences on the force required. We therefore expect that there is some angle `theta at which the force is minimized.
The force function, which is derived from physics, is as shown below. We note that this function is a composite f(g(`theta)) of g(`theta) = sin(`theta) + `mu cos(`theta) and f(x) = 1/x.
We proceed to maximize the function F(`theta). We first take the derivative, then set the derivative equal to zero to find the critical point. The equation for the critical point is easily simplified by dividing both sides by the quantity m g `mu, first noting that this quantity is always nonzero and that it is therefore safe to divide both sides by the quantity. We then note that for values of `theta between zero and 90 degrees, which are the only angles relevant in this situation, the denominator can never be zero and we can therefore multiplied both sides by this denominator. We obtain the equation cos(`theta) - `mu sin(`theta) = 0, which we easily rearrange to obtain tan(`theta) = 1/`mu, so that `theta = tan^-1(1/`mu).
The second derivative of F is a mess; try it and you'll see that a first derivative test is probably the way to go. Since the sign of the derivative will be that of the numerator cos(`theta) - `mu sin(`theta), we easily see that the derivative is negative for `theta > tan^-1(1/`mu), and positive for `theta < tan^-1(1/`mu), so that the critical point is a maximum.
"