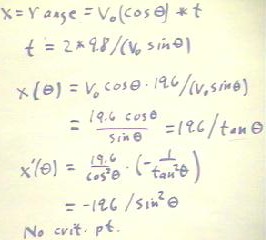
The quiz today asserted that a projectile starts out with an initial x velocity of v0 cos(`theta), and an initial y velocity such that the projectile remains in the air for time t = 2 * 9.8 / (v0 sin(`theta)). Note: the physics of these assertions is incorrect; the time should be t - 2 * v0 sin(`theta) / 9.8.
The problem was to determine the angle `theta at which the maximum range would occur, and to find the maximum range.
Using the (incorrect) assumptions, we can easily see that if x = v0 cos(`theta) * t and t = 2 * 9.8 / (v0 sin(`theta)), then x can begin as a function of `theta alone by x(`theta) = v0 cos(`theta) * 2 * 9.8 / (v0 sin(`theta)) = 19.6 / tan(`theta), as shown below.
To maximize this function we would first take its derivative with respect to `theta, finding that x'(`theta) = -19/6 / sin^2(`theta). If we set this expression equal to zero, we will find that there is no solution. There are therefore no critical points.
We find, in fact, that as `theta -> 0, tan(`theta) -> 0 and that x(t) = 19.6 / tan(`theta) must therefore approach infinity. So it is clear that there can be no maximum for the function we have obtained here.
Recall that we stated that the physics of the problem as originally posed was incorrect, and that we should have had t = 2 * v0 sin(`theta) / 9.8. We proceed to solve the problem for the correct expressions.
The correct expressions are shown below, and we easily obtain x(`theta) = v0^2 cos(`theta) sin(`theta) / 4.9.
To find critical points we set the derivative x'(`theta) = (v0^2 / 4.9) (-sin^2(`theta) + cos(`theta)) equal to 0. Since the first factor v0^2 / 4.9 can never be zero, we conclude that the only solutions occur when the second factor -sin^2(`theta) + cos^2(`theta) = 0.
From this equation we quickly obtain sin^2(`theta) = cos^2(`theta); dividing both sides by cos^2(`theta) we obtain tan^2(`theta) = 1, so tan(`theta) = +- 1, and `theta = -45 deg, or 45 deg, or 135 deg, or 225 deg. Since we are talking about firing a projectile from ground level, the only sensible solution is `theta = 45 deg (we won't fire it backwards, or into the ground, or backwards into the ground).
It is probably easiest to use the first-derivative test. Since v0^2 / 2 is positive, the derivative will have the same sign as -sin^2 (`theta) + cos^2 (`theta). At `theta = 45 deg, the sine and cosine are both equal. For angles a bit less than 45 degrees, the sine is less than the cosine; for angles a bit more than 45 degrees the sine is greater than the cosine. It follows that for angles less than 45 degrees the derivative is positive and for angles greater than 45 degrees the derivative is negative, which tells us that the function has a maximum at its 45 degree critical point.
Of course we could have taken the second derivative, obtaining x''(`theta) = v0^2 / 2 ( -4 * sin(`theta) cos(`theta) ), which is negative for `theta between 0 and 90 deg. This implies that the function is concave downward at its 45 deg critical point, and therefore has a maximum at that point.
The Completeness Axiom
Suppose we have the graph of a big ugly polynomial (abbreviated B.U.P.). Any polynomial is in fact a thing of beauty, but let us suppose that we are trying to find the zeros of this polynomial. We see that there are at least five zeros, and the process of trying to find them might well render us blind to its virtues. In fact, in might well occur that one or more of the zeros of this polynomial cannot be expressed in any exact form.
If in frustration we have resorted to numerical approximations of zeros of the polynomial, we might well find something like the situation depicted below. We might determine that the polynomial is less than 0 when x = 1.31 and greater than 0 when x = 1.34. We therefore feel confident that there is a zero between these points. In that case, we will say that if z is the zero, 1.31 < z < 1.34.
We might subsequently find that the polynomial is negative at x = 1.325 and positive at x = 1.335. We will then say with some confidence that there is a zero such that 1.325 < z < 1.335.
It is clear that we could use some enlightened process of trial and error to obtain smaller and smaller intervals containing z. And we would have confidence that, if the process was continued indefinitely, we could 'home in' as closely as we desired to the actual value of z.
Now, just what is it that makes us think that this process really converge is to some specific number z? And what makes us think that even if there is such a number, when we plug it into the polynomial we will in fact get 0? These things seem obvious, but there is no way to prove that they are in fact true.
Without making some assumptions, mathematicians cannot in fact verify either of the assertions implied in the preceding paragraph. We cannot prove that the process really converge us to some specific number, and we cannot prove that even if it did the number would in fact give us 0.
In a situation like this mathematicians try to find the simplest and most obvious statement from which the assertions in question can be proved. The statement that has been accepted by mathematicians is that any set of numbers which has an upper bound (i.e., and number that the set cannot exceed) has a least upper bound (i.e., an upper bound such that no other upper bound can be less).
This statement is called the 'completeness axiom'. It is an axiom in that it expresses something which we choose to believe firmly is true, must in fact be true if our understanding of mathematics is to make any sense at all, but which we cannot prove.
In the figure below we see that the set of numbers which are less than the presumed zero z of our example is bounded above by 1.34, then by 1.335, then presumably by an infinite set of decreasing numbers. Thus, the set of numbers which are less than z can contain no number greater than 1.34; cannot in fact contain no number greater than 1.335; cannot in fact contain any of the numbers in the infinite decreasing set that we get by 'squeezing in' by the process described above.
By the completeness axiom, since the set of numbers less than z has upper bounds, this set must have a least upper bound. And it will be this least upper bound that we identify with the zero of the polynomial.
The Nested Interval Theorem
The Nested Interval Theorem follows from the Completeness Axiom, in that it can be proved from this axiom. Statements that can be proved from our axioms, or from other statements that can be proved from our axioms, are called Theorems.
The intervals that we obtained earlier our examples of nested intervals. As depicted in the figure below, the interval (1.31, 1.34) completely contains the interval (1.325, 1.335). We thus say that the second interval is 'nested' within the first.
The Nested Interval Theorem states that if we have an infinite sequence of nested intervals, then there exists at least one number common to all the intervals.
Note: The backward E in the statement below is shorthand for 'there exists'. The statement is read 'there exists at lease one number common to all' (meaning to all intervals).
Using the Nested Interval Theorem, we might for example say that the zero z of our original polynomial is the unique point common to the set of nested intervals obtained by the process used to obtain the first two such intervals.
The Intermediate Value Theorem
The Intermediate Value Theorem can be proved from the preceding axioms and theorems. It states something like this: If a function y = f(x) is continuous on an interval (a,b) of the x axis, then it must take every y value between f(a) and f(b).
A more precise mathematical definition says that for such a function, given any value y = k between f(a) and f(b), there exists and x value between a and b such that f(x) = k.
In the figure below we give a briefer and less precise statement next to the graph, where we have indicated k between f(a) and f(b) on the y axis and the corresponding x between a and b on the x axis. The backwards E is again read 'there exists', and the | stands for 'such that', so that the statement is read "Given k between f(a) and f(b), there exists an x (between a and b, not stated but implied in the brief statement) such that f(x) = k.
Definition of a Limit
We have used the idea of limits to obtain expressions for the derivatives and integrals of various functions, and to to otherwise examine the behavior of functions and the precision of various approximations.
For example, very early in the course we used the fact that the limit as `dx -> 0 of the expression (2 a x `dx + b `dx) / `dx = 2 a x + b was equal to the sum of the limits of 2 a x and b (the idea that the limit of f(x) + g(x) is equal to the limit of f(x) + the limit of g(x)). We have used other properties of limits, usually with the warning that it is a good idea to be a bit uncomfortable with some of the operations we have performed.
To put the use of limits on a firmer base, we need to make a formal definition of exactly what it is we mean when we take the limit of a function as the variable approaches some fixed number.
We begin with the main idea, which we will then put into precise mathematical form.
The main idea is this. We say that the function f(x) approaches a limit b as x approaches a number a, if by 'squeezing' x sufficiently close to a, we can 'squeeze' f(x) as close as we desired to b.
The figure below shows a graph of a typical function. We assumed for this function that f(a) = b, and that the function is represented accurately by a continuous graph over some interval of x values surrounding a.
We imagine that we want the values of f(x) to remain near b. We say that lim[x -> a] f(x) = b if, no matter how close we want to remain to b, there is a neighborhood of a such that whenever x use in this neighborhood, f(x) will be within the specified closeness to b.
Now we get a bit more precise. The closeness of f(x) to b will be specified by a number `epsilon, which looks sort of like a small rounded E, so that we will be looking to make f(x) stay within `epsilon of b. We will do this by restricting x to stay within `delta of x = a (we will use the lowercase Greek delta, which doesn't look like a triangle but like a d with a hooked and rounded stem).
The task will be to specify the `delta that goes with a given `epsilon, for whenever function we are looking at. If we can show that for some `epsilon it is impossible find such a `delta, we will conclude that the limit does not exist.
The figure below gives this definition. We will see examples of the application of the definition of limits during the next class meeting.
The definition in the figure should read "lim[x->a] f(x) = b if for any `epsilon, there exists a `delta such that whenever | x-a | < `delta, | f(x) - b | < `epsilon." This definition can be paraphrased using the phrase "if x is `delta-close to a, then f(x) is `epsilon-close to b".
Note that | x - a | < `delta means that x lies between a - `delta and a + `delta: a - `delta < x < a + `delta. This inequality describes an interval of the x axis centered at x = a, and extending a distance `delta to the left and right of x = a.
Similarly, | f(x) - b | < `epsilon means that f(x) lies in an interval of the y axis centered at y = b and extending a distance `epsilon to above and below y = b.
The figure below depicts these statements.
