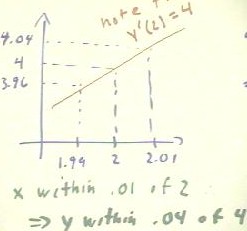
The quiz problem asked how close y would be `squeezed' to y = 4 if x was `squeezed' to within .01 of 2, and then how close x would have to be `squeezed' to the value x = 2 in order to account with the goal of `squeezing' y to within .01 of 4.
We see that if x is within .01 of x = 2, then 1.99 < x < 2.01. It follows that 1.99^2 < x^2 < 2.01^2, or 3.9601 < x^2 < 4.0401. Thus y = x^2 lies between 4 - .0399 and 4 + .0401, and we can say that y is within .0401 of 4. To a good approximation, we can say that y is within .04 of 4, as expressed in the figure below.
We note in passing that the extent of the y interval is approximately 4 times that of the x interval. From our knowledge of derivatives and tangent line approximations, we know that the slope of the line tangent to the graph of y = x ^ 2 at the point (2,4) must be 4, so we would expect this ratio. However, we should not use this knowledge to determine these intervals. The reason is that we are studying limits and other foundations of the calculus, which justify what we think we know about derivatives, integrals and their applications. If we use what we think we know to justify what we think we know, we have just gone in a circle. While this is standard practice in interpersonal relationships and politics, it is a very bad idea in mathematics, science and any other field in which we wish to claim that our knowledge is well founded.
To restrict y within .01 of 4, we would have 3.99 < y < 4.01, or 3.99 < x^2 < 4.01. Taking square roots we see that 1.975 < x < 2.025 (approximately). We can thus say that to a good approximation, if x lies within .025 of 2, y will lie within .01 of 4.
We could in fact use a stronger `squeezing` of x, and say that if x lies within .02 of 2, then certainly y will lie within .01 of 4.
An important point here is that we are not trying to find the precise boundaries on x which will ensure that y lies within the specified interval, but rather that we are simply trying to find boundaries within which we are sure that y lies within the specified interval.
We now turn to the problem of restricting y to within `epsilon of y = 4. We will do so by finding a number `delta such that whenever x is within `delta of x = 2, y will be within `epsilon of y = 4.
We start by looking at what happens if we restrict x to within `delta of x = 2.
If x is within `delta of x = 2, then
2 - `delta < x < 2 + `delta.
It follows that
(2 - `delta) ^ 2 < x^2 < (2 + `delta) ^ 2, or
4 - 4 `delta + `delta^2 < x^2 < 4 + 4 `delta + `delta^2.
Now, if `delta is small, `delta^2 will be very small and to a good approximation we can say that
4 - 4 `delta < y < 4 + 4 `delta.
What we want to be able to say is that
4 - `epsilon < y < 4 + `epsilon.
So it is almost safe to say that for small `epsilon, we can use `delta = `epsilon / 4.
If we strengthen our condition on `delta to say that `delta = `epsilon / 5, then we would conclude that
4 - 4 `delta + `delta^2 < x^2 < 4 + 4 `delta + `delta^2, or
4 - 4 * `epsilon / 5 + (`epsilon / 5)^2 < y < 4 + 4 * `epsilon / 5 + (`epsilon / 5) ^ 2.
As long as 4 * `epsilon / 5 + (`epsilon / 5) ^ 2 < `epsilon, this will give us the desired result: 4 - `epsilon < y < 4 + `epsilon.
Since
4 * `epsilon / 5 + (`epsilon / 5) ^ 2 < `epsilon
can be rearranged to give us
(`epsilon / 5) ^ 2 < .2 `epsilon,
which can then be rearranged (divide by `epsilon) to give us
`epsilon / 25 < .2,
we can safely say that whenever `epsilon < 5, the desired inequality is obtained and y is `squeezed' within `epsilon of 4 when x is `squeezed' within `epsilon / 5 of 2.
There was nothing sacred about the choice of `delta = `epsilon / 5. We could have used any `delta which is less than `epsilon / 4 and obtain similar results. For any such `delta we would have found some number such that whenever `epsilon is less than that number, we obtain the desired squeezing.
Definition of the limit
From the definition of the limit, we can prove the limit properties we have been using all along (hopefully with a feeling of vague discomfort). These properties are listed in your text, but tell us for example that lim [x -> c ] ( f(x) + g(x) ) = lim [ x -> c] f(x) + lim [ x -> c] g(x), with similar statements for products, quotients and scalar multiples of functions. You should know the specifics of these properties, including the conditions under which they are valid.
The definition of the limit of a function f(x) as x approaches a number c is as follows: L = lim [x -> c] f(x) if, given any number `epsilon, however small, there exists a number `delta such that whenever | x - c | < `delta, it follows that | f(x) - L | < `epsilon.
The figure below depicts the intervals for which | x - c | < `delta and for which | f(x) - L | < `epsilon. We imagine that as x ranges over the entire interval c - `delta < x < c + `delta, the value f(x) will always fall between L - `epsilon and L + `epsilon. Our task in finding any limit is to show that, given any number `epsilon, we can find `delta to make it so.
Informally, we say that we will be within`epsilon of L whenever we are within `delta of c.
It follows that if it is impossible to find such a `delta for some `epsilon, the limit does not exist.
Consider the example below, which is discussed in your text. We wish to determine whether lim [x -> 2] | x-2 | / (x - 2) exists and, if so, what its value is.
To understand the function | x - 2 | / ( x - 2 ) near x = 2, we might make a table such as the one below. When we evaluate the function for x = 1.9, we obtain | 1.9 - 2 | / (1.9 - 2) = .1 / -.1 = -1. Evaluating the function for x = 2.1, we obtain .1 / .1 = 1. We see fairly quickly that any time x is greater than 2, our function will be +1 and whenever x is less than 2 the function will give us -1.
The graph of this function is shown below.
Now, if we wish to determine the limit of this function as x approaches 2, we have to be able to restrict the values of the function to within `epsilon of some limiting value, for any `epsilon we might choose. However, when we restrict x to an interval (x - `delta, x + `delta), we cannot help but get y values of -1 and 1. This should be clear because any such interval will contain points for which x < 2, which will give us f(x) = -1, and other points for which x > 2, which will give us f(x) = +1.
Since these x values differ by 2, it will be impossible to restrict f(x) to within `epsilon of any value whenever `epsilon < 2.
It should be clear that for any function which has a 'jump' like that we have just seen, a similar argument will show that whenever `epsilon is less than the 'jump', we will be unable to restrict the value of the function in a neighborhood of the 'jump' to within `epsilon of any proposed limiting value.
We can speak of right-and left-hand limits. A right-hand limit at x = c seeks to restrict the function to within `epsilon of a limiting value by restricting x to within an interval c < x < c + `delta. Note that this interval does not include the point x = c.
For the function of this example, we can easily find the right-hand limit at x = 2. For any interval 2 < x < `delta, for any `delta, the function will take the value 1 at every point of the interval. So the right-hand limit must be 1.
Note that this limit exists even though the function itself is not defined at x = 2.
Similarly, the left-hand limit at x = 2 is easily seem to be -1.
Since the right-hand and left-hand limits both exist and are not equal, we conclude that a 'jump' in fact exists and that therefore the limit of the function does not exist.
We next consider limit of the function y = sin(1/x) at x = 0.
To obtain an understanding of this function, note that whenever 1/x changes by 2 `pi, sin( 1/x ) will go through a complete cycle, and that in each cycle y will take the values 1 and -1.
Now note the fact that as x -> 0, 1/x -> infinity. This means that 1/x will change by 2 `pi an infinite number of times in any neighborhood of x = 0.
More specifically, if we restrict x to an interval (0 - `delta, 0 + `delta), 1/x will take every value greater than 1 / `delta (and also every value less than -1 / delta, though we will not use that fact here). Again, we see that 1/x will change by 2 `pi and unlimited number of times in this interval, so again sin(1/x) will go through an unlimited number of complete cycles in this interval.
The graph of the function is depicted below.
From what has been observed above, we see that for any `delta, the function y = sin ( 1/x ) will take all values between -1 and 1. More specifically, it will take the values -1 and 1, which makes it impossible to restrict its values to within `epsilon of any proposed limit whenever `epsilon < 2. So we see that the limit does not exist.
It should be clear that in this case, the right-and left-hand limits at x = 0 do not exist either, because any interval 0 < x < `delta or -`delta < x < 0 must necessarily contain complete cycles of the function.
We can say that in any neighborhood of x = 0, y can only be squeezed between -1 and 1 and no closer.
Definition of Continuity
We say that a function is continuous at a point x = a if its limit at that point exists, and give that limit is equal to the value of the function at that point.
By this definition, it is fairly easy to show that any polynomial, exponential, sine or cosine function is continuous at every point x = a. These functions have smooth and continuous graphs; the definition of continuity is motivated by this property of such graphs.
Recall how limits extend to sums, products, constant multiples and quotients of functions. It actually follows from these limit properties that continuity extends to sums, products, constant multiples and quotients of functions, in the sense that if to functions are continuous at a point or on an interval, their product, sum, and constant multiple functions will be continuous at that point or on that interval. The same can be said about their quotients, provided the denominator function never takes the value 0 at the point or on the interval, as the case may be.
We also note that continuity applies to composite functions. The statement in the text regarding continuity of composite functions is not quite accurate. A better statement might be the following:
If the function g(x) is continuous over some interval, and if f(x) is continuous over the corresponding range of the function g(x), then the composite function f(g(x)) is continuous over the original interval.
Contrast this with the statement in the text, which simply states that the two functions are continuous over some interval. If the function g(x) had y values that were not in this x interval, then we might be stuck trying to evaluate f(x) at a point where it is not continuous, or perhaps not even defined.
For example, we could have f(x) = `sqrt(x) and g(x) = 5 - x. Both functions are defined on the interval 0 <= x < 10, for example, but if x > 5 g(x) will be negative and composite f(g(x)) is not even defined. So clearly the composite is not continuous on the original interval (recall that continuity at a point requires that the function have a value at that point).
Definition of Differentiability
Recall that we have defined the derivative of a function f(x) in terms of the limit at `dx = 0 of the difference quotient [ f(x + `dx) - f(x) ] / `dx. We will say that a function is differentiable at a point x if this limit exists.
As an example of a function that is continuous but not differentiable at a point, consider the absolute-value function f(x) = | x | at x = 0. Its derivative at x = 0 is defined as lim [`dx -> 0] { f(0 + `dx) - f(0) } / `dx.
If `dx > 0, f(0 + `dx) - f(0) } / `dx = { | `dx | - 0 } / `dx } = `dx / `dx = 1.
On the other hand if `dx < 0, | `dx | = - `dx (note that under these conditions -`dx will be positive) and the difference quotient will be equal to -1.
It follows that the right-hand and left-hand limits are + 1 and -1, respectively, so that the limit defining the derivative does not exist. The absolute-value function therefore has no derivative at x = 0.
The graph of the function, as depicted below, shows is clearly that the function has a slope (and therefore derivative) of -1 for x < 0 and a slope (and therefore derivative) of 1 for x > 0. At x = 0, however, we cannot determine by looking at the graph what the slope should be; and from what we have just seen it becomes clear that there is no limit and hence no derivative at this point.
The Error of the Tangent-Line Approximation
We are familiar with the tangent-line approximation to a function. Through a point (a, f(a) ) on the graph of a differentiable function f(x), we construct a straight line with slope f'(a). Then at a point x, this straight line will take value f(a) + f'(a) * (x - a), which is the tangent-line approximation to the value of f(x).
The error E(x) of the approximation is the difference between the actual value of f(x) and the tangent-line approximation f(a) + (x - a) f'(a).
It is fairly easy to prove that E(x) not only approaches 0 as x -> a, which it certainly must because both the function and the tangent-line approximation take the same value f(a) at x = a, but that as x -> a the ratio E(x) / (x - a) approaches 0. Thus the error term disappears even as a proportion of the disappearing quantity x - a.
We obtain this result by simply rewriting E(x) / (x - a) as { f(x) - [ f(a) + f'(a) (x-a) ] } / ( x - a ) and doing a little algebra, while keeping in mind the definition of the derivative. The details are in your text.
Review
In reviewing for the upcoming test, be sure you are very familiar with the most basic concepts and operations studied in chapters 4 and 5. The test will not be limited to these basic ideas and procedures, but if they are fairly well mastered you'll be assured of at least passing the test with a C.
The topics include the following:
Derivatives of the basic functions
Derivatives of composite functions
Applications
Implicit differentiation
Linear approximation and l'Hopital's Rule
Be able to find and apply knowledge of the local and global maximum and minimum points of a function.
"