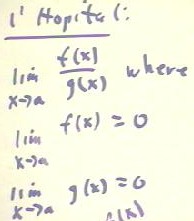
Test Version 27
Show all work and document your analysis.
You will be given a grade for problems 1-10.
Each additional problem will be counted if and
only if it increases your score.
1. Find f'(x) if f(x) = 2 e^x - 4 arctan x + 4 / x^3.
2. The period of a pendulum is T = 2 `pi `sqrt(g / L), where L is the length of the pendulum. Find dT / dL. What is the significance of the sign of dT / dL?
3. Find all local maxima, minima and inflection points for the function y = (x - 2) (x^2 - 4x - 5), and indicate all on a graph of the function.
4. Show how to use the chain rule to obtain the formula for the derivative of the function y = x^.1 from the formula for the derivative of y = x^10.
5. Determine the location of the minimum point of the function y = x^2 + k x + 2, and show that for the family defined by this function for all values of k, the minimum points all lie on the same parabola.
6. Using a sketch accompanied by a thorough explanation, tell how l'Hopital's Rule is obtained from consideration of local linearizations.
7. Using a sketch accompanied by a good explanation, obtain the expression for the equation of a tangent line through the point (a, f(a)), if the derivative of the function f(x) at x = a is f'(a).
8. The function f(x) = sin (.01 `pi (100 - x^2)) * `sqrt(100 x^4 + x^6) is to be maximized. Show that between x = 0 and x = 10 this function is positive, while at x = 0 and x = 10 it is 0, and explain how this implies that there must be at least one maximum between 0 and 10. Find the derivative of f(x) and plot f'(x) using DERIVE. Use the plot to estimate critical point(s) and behavior at critical point(s) to determine where the maximum value of this function occurs.
9. Use implicit differentiation to find the derivative dy/dx for x = -2 and y = 1, when y is defined implicitly by the equation x^2 y^3 - x^3 y^5 = 12. Find the equation of the line tangent to the graph of y(x) at the corresponding point, and determine the approximate value of y for x = -2.2. Determine how well the resulting values fit the equation.
10. If a projectile is launched from the ground at velocity v0 and at angle `theta from the horizontal, it will require a time interval `dt = 2 v0 sin(`theta) / 9.8 to return to the ground, during which time it will travel in the horizontal direction at a constant velocity of vx = v0 cos(`theta). Find the expression that shows how far the projectile travels in the horizontal direction, and find the optimum angle required for maximum projectile distance.
11. Find the derivative of y = 3 cos x * x^.7 - 5 e^x / 7 cos(x).
12. Work is defined as the product of force and distance. If the force required to move away from Earth against gravity is inversely proportional to square of distance from the center of the Earth, and if the force required for a 160-lb individual at a distance of 6.4 million meters from the center is about 700 Newtons, then what is the force required at distance r? How much work is therefore done against gravity in moving from 6.4 million meters to double that distance from the center of Earth?
13. Find the derivative of y = 3 cos (x^.7) - 5 e^( 7 cos (x) ).
14. Local linearizations tell us that f(x+h) is approximately equal to f(x) + f'(x) * h and g(x+h) is approximately equal to g(x) + g'(x) * h. Use this fact and the definition of the derivative to obtain an expression for ( f(x) g(x) ) '. (You are deriving the formula for the product rule; don't use the product rule to get your result).
15. Using the definition of the derivative, obtain the expression for the derivative f'(x) of f(x) = a x^2 + b x + c.
16. Find each of the following limits: lim[x->0] (e^x / x^4), lim[x->0] (x^2 / (e^x - 1) ), lim [x->0] ((1-cos x) / sin^2 (x) ), lim [x->0] ((1 - cos x)^3 / sin x).
(Notes to be expanded later)
Problems in decreasing order of difficulty, as rated by class:
Prob. # 4: l'Hopital applies only when limit of both fns. is zero.
In this case both graphs pass thru x axis at same point. Near that point the local linearizations become better and better approximations.
When very close, the ratio f(x) / g(x) of values is very near the ratio of the slopes of the local linearizations.
Difference between local lin. and function becomes more and more insignificant. Then f(x) / g(x) very close to ratio [ f'(a) (x-a) + f(a) ] / [ g'(a) (x - a)] of local linearizations.
Condition for rule was f(a) = g(a) = 0. So f(a), g(a) disappear from num. and denom.. Result is f'(a) / g'(a), as in rule.
Prob. # 12: Given work = force * dist. (sum of F `dx since force changes with dist.), and force inv. prop. to square of dist. (F = k / x^2), F = 700 N when x = 6.4 * 10^6 m. Solve proportionality to get k, obtain force as function of x.
Integrate F dx (summing process for F `dx contributions, taken to limit). Antiderivative of 1/x^2 is -1/x, since (-1/x)' = 1 / x^2. x1 and x2 are starting and ending values of x (6.4 * 10^6 m and double that in present problem).
Prob. 16: First limit form 1 / 0, gives infinite limit. Second form is 0 / 0, so use l'Hopital; get 0/1 = 0.
3d limit 0 / 0; use l'Hopital. Fourth line looks good (just cancel sin x and get 1/2), but invalid because can't have g(a) = 0. Apply l'Hopital to 3d line instead; get limit of cos(x) / [ 2 (cos^2 x - sin^2 x) ], equal to 1 / 2 at 0. Got same answer as with wrong procedure, but often that won't happen.
Prob. 14: Problem says to use def. of derivative, so write it down (1st line). Then says to use local lin. for f(x+`dx) {prob. says f(x+h) -- same thing, slight adjustment in notation}. Substitute local lin. in line 2. Do algebra in lines 3 and 4 (start writing just f, g, f' or g' instead of f(x), g(x), f'(x), g'(x) -- the x dependence is understood). The desired result falls into our hands.
Prob. 4: The problem people had with this one was noticing that x^.1 and x^10 are inverse functions. Then the familiar process comes to us. g(x) = x^.1 (the fn. whose derivative we want to find); f(x) = x^10 (the inverse of that function, whose derivative we know). Derivative of composite is 1. Derivative by chain rule is g'(x) f'(g(x)). f'(g(x)) we know. Set equal to 1 and solve for g'(x). The result is just what the power function formula says, but that formula was proved only for integers. Now we can justify it for reciprocals of integers by means similar to those used here.
Prob. 7: We sketch the point (a, f(a)) and a line of slope representing f'(a). If x is a point on this line, the between (a, f(a)) and (x,y) the slope is (y-f(a)) / (x-a) = f'(a), so y = f`(a) * (x-a) + f(a). An alternative view is that if we move over thru displacement x-a, we move up rise = slope * run = f'(a) (x-a) and end up at y = f(a) + rise = f(a) + f'(a) (x-a).
"