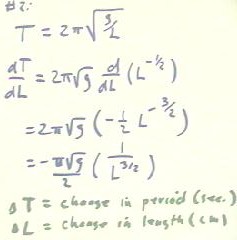
Problem #2 stated (incorrectly) that the period T of a pendulum is T = 2 `pi `sqrt(g / L). [The actual expression should be 2 `pi `sqrt(L / g); clearly a longer pendulum has a greater period, not a shorter. Excuse the typo.]
The derivative of T with respect to L is calculated below. We interpret the derivative as the change in the period T, in seconds, per unit of change in length L, in cm.
For example, if dT / dL = -.04 sec / cm, then a 2 cm change in length will result in a change of 2 cm * -.04 sec / cm = -.08 sec in period. This means that the period is getting shorter as the length is increasing (again, this is wrong; but it is the conclusion that follows from the function T given in the problem).
Problem #8: The function f(x) is the product of sin(.01 `pi (100-x^2)) and `sqrt(100 x^4 + x^6). The first factor is zero when x = 10, since sin(0) = 0, and also when x = 0, since sin(`pi) = 0; as a result the entire function will be zero, since we multiply by factors. The second factor is also zero when x = 0.
Between x = 0 and x = 10, the argument of the sine function will be between 0 and `pi, so the sine function will be positive. Since the square root must always be positive, we see them that f(x) is positive between x = 0 and x = 10.The derivative of the function is easily found as the product of the derivative of the two factors.
It is pretty much hopeless to try to find the zeros of the derivative function by solving the equation that results when we set f'(x) equal to zero. Instead we go to DERIVE and plot the derivative function, observing that the critical point occurs when this derivative function is 0. And estimate from the graph shows that the derivative is zero at approximately x = 8.2, and that the derivative goes from positive to negative that this point. This indicates, by the first derivative test, that the critical point will be a maximum.
The figure below shows the approximate DERIVE plot of the derivative in the graph to the left, and of the function as well as the derivative in the graph to the right. We see that the function does indeed have a maximum at the point for the derivative is zero.
If the range of a falling ball x is equal to the product v0x `dt, and if v0x = v0 cos(`theta) while `dt = 2 v0 sin(`theta) / 9.8, then we see that the range x is a function of `theta, with x(`theta) = .2 v0^2 cos(`theta) sin(`theta) (the .2 is approximate; the actual value would be closer to .196).
To find the angle at which the range of the ball is maximized we find the critical point where dx / d`theta = 0. Having found the critical point we will probably use the first derivative test to determine whether we have a maximum or a minimum, since the second derivative will require a bit more algebra.
The first derivative will be .2 v0^2 ( cos^2(`theta) - sin^2(`theta) ), which is zero when cos^2(`theta) = sin^2(`theta). For positive angles between 0 and 90 deg, this occurs when `theta = 45 deg. This problem was essentially done in recent class notes.
Problem #5:
The function family defined by y = x^2 + kx + 2 has derivative dy / dx = 2 x + k, with a critical point when 2x + k = 0. This occurs when x = - k / 2. Since the second derivative is d^2 y / dx^2 = 2, the graph is always concave upward so the critical point occurs at a minimum.We see therefore that the minimum point of a function of this family lies where x = - k / 2 and y = x^2 + kx + 2 = (-k/x)^2 + k (-k/2) + 2. The point at which the minimum occurs is therefore (x, y) = ( - k / 2, (-k/2)^2 + k (-k / 2) + 2). If we simplify the second coordinate we see that the minimum of occurs at
min. pt. = ( - k/2, - k^2 / 4 + 2).
Now when x = -k/2, k = - 2x. So the y coordinate could be written y = - k^2 / 4 + 2 = - (-2x)^2 / 4 + 2 = - x^2 + 2.
We therefore see that the minimum points for the family lie on the curve y = - x^2 + 2.
Note error in figure: The last three lines of the figure have left out the - sign in front of the term - k^2 / 4; as a result the figure asserts that the parabola is y = x^2 + 2, rather than the correct y = - x^2 + 2.
In the figure below we perform an implicit differentiation on the indicated equation. The steps are standard and should be straightforward.
We find the equation of the tangent line at (-2, 1) by first calculating y' at this point. We obtain y' = 4/13.
We then obtain the slope = slope equation (y - 1) / (x - (-2) ) = 4/13 of the tangent line. Solving for y we obtain y = 4/13 x + 21/13.
Using the tangent line to approximate the value of the function at x = - 2.2, we perform a straightforward substitution to obtain y = 61 / 65.
Substituting x = - 2.2 and y = 61/65 into the equation, the right- and left-hand sides should be close but will probably not be exactly the same. Recall that the tangent line approximation is merely an approximation; the equation gives us no reason to expect that the function y(x) defined implicitly by the equation will be linear.
Problem #1:
We easily take the derivative of the indicated function, as shown in the figure below.
Problem #3:
We easily take the derivative of the indicated function, as shown in the figure above.
The given function can be multiplied out to give us the indicated expression. The derivative is easily calculated.
Setting the derivative equal to zero we obtain a quadratic equation with solutions x = 2 +- `sqrt(3).
In the figure below we obtain the expression for the second derivative. The second derivative is clearly 0 when x = 2. If we set y'' > 0, we obtain 2x - 4 > 0 or x > 2; similarly we obtain y'' < 0 if x < 2.
A graph of the derivative function y'(x) will therefore have zeros at x = 2 +- `sqrt(3) and a minimum at x = 2; the derivative will change from decreasing to increasing at the minimum point. For the function y(x), all this implies extreme points at x = 2 +- `sqrt(3) and an inflection point at x = 2. At the critical point 2 - `sqrt(3) the derivative goes from positive to negative so the critical point will give us a maximum, while at the critical point 2 + `sqrt(3) the derivative goes from negative to positive and the critical point gives us a minimum.
The resulting behavior of the function is indicated in the graph below.
We note that the original function has factored form y = (x - 2) ( x + 1) ( x - 4), with zeros at x = -1, x = 2 and x = 4. These zeros are not accurately indicated in the graph above. You should risk extra graph to indicate the zeros as well as the y intercept.
"