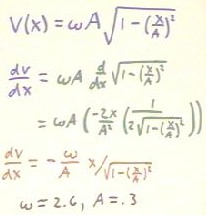
The velocity of a pendulum changes as it swings back and forth, with velocity 0 at the extreme points of its swing (where it stops for an instant before swinging back in the opposite direction) and a maximum velocity at the center of its swing (the position where it would hang naturally without moving).
If x is the distance from the center point of the swing, A the distance from an extreme point to the center point of the swing and `omega (the Greek letter that look something like a rounded w) equal to 1/(2 `pi) times the period of the motion (the time from an extreme point to the other and back), then the velocity at position x is given by the function v(x) = `omega A `sqrt( 1 - (x/A)^2 ).
We ask for the derivative dv / dx and an interpretation of this derivative.
The derivative is easily know calculated, as shown in the second third lines below, using the chain rule. If non-constant part of the velocity function is f(g(x)) with f(x) = 1- (x/A)^2 and f(z) = `sqrt(z), we see that g'(x) = (1 - x^2 / A^2)' = -2x / A, and f'(z) = 1 / (2 `sqrt(z)), so that the derivative is as given below.
To interpret the derivative we note that `dv would be a change in velocity while `dx would be a change in position, so that the derivative is that change in the velocity of the pendulum per unit change in its position.
For the pendulum used in class as an example, `omega = 2.6 and A = .3 meters.
For this specific pendulum we obtain by a straightforward substitution the function dv / dx depicted below. We ask what the change `dv in velocity would be as the position x changes from .20 m to .22 m. That is, how much faster or slower with the pendulum removing at the x = .22 m position than the .20 m position. From our experience that the velocity of a pendulum decreases as moves further away from its central position, we conjecture that the velocity will decrease as we move from x = .20 m to x = .22 m.
We need to find dv /dx in the vicinity of the x = .20 m to x = .22 m positions. We expect to get a good estimate if we use the midpoint value of x, x = .21 m. At this position we calculate dv / dx = - 2.5, as shown below.
We interpret this result as telling us that near x = .21 meters, `dv / `dx will be close to - 2.5 m/s per meter of position change. From this interpretation in would follow that .02 m of position change would give us a change in x of `dx = .02 meter ( -2.5 m/s / meter) = -.05 m/s. That is, the change is speed should be about -.05 m/s as we move from x = .20 m to x = .22 m.
We could easily check this by using the v(x) function to calculate the velocity at the two points. We would obtain `dv = v(.22) - v(.20), and our result should be close to -.05. You should check this out.
`01
We now take another look at the concept of marginality. If R and C in the figure below depict the graphs of revenue and cost vs. number of widgets, we look for the point of maximum profit. The red arrow from the cost graph to the revenue graphs represents the profit at a point where cost is increasing a bit faster than revenues, as indicated by the slightly greater slope of the cost graph at this point (the red lines represent tangent lines at this point). Since cost is increasing faster than revenue, we conclude that profits must be decreasing at this point and that we are beyond the point of maximum profit.
At the position of the green arrow, we see that the slope of the revenue graph is greater than that of the cost graph and conclude the revenues are increasing faster than costs. As a result we conclude that profits are increasing at this point, and that we have not yet reached our maximum profit.
The approximate position of maximum profit is indicated by the black arrow, labeled 'max profit'. The tension lines are not drawn at this point, but it is very plausible that they are parallel so that the revenue and cost functions are both increasing at the same rate. It follows that the profit function is neither increasing nor decreasing at this point. Since the profit is increasing to the left of this point and decreasing to the right, we therefore conclude that the profit function is a relative maximum at this point.
The graph below shows the marginal revenue vs. marginal cost for the cost and revenue functions shown in the graph above. The marginal revenue at a point is a slope of the revenue graph; from the graph above we see that this slope is decreasing so that the graph of marginal revenue must be decreasing. Similarly the slope of the cost graph in the figure above is increasing, so we conclude that the marginal cost graph will be increasing.
As we saw above, the maximum profit occurs a point where cost and revenue are increasing at the same rate, i.e., at a point where marginal cost equals marginal revenue. As a result, at this point the marginal profit function `pi(t) = MR - MC will be 0. Furthermore, the marginal revenue must be increasing faster than the marginal cost to the left of the point and slower to the right, which implies that the marginal profit MR - MC must be decreasing. A decreasing function is positive to the left and negative to the right of a point at which the function is 0. This is clearly the case for the situation depicted above.
The graph below shows marginal cost and marginal revenue graphs. We ask at what point the profit should be a maximum.
We can apply the ideas just developed to determine which of the points a and b at which marginal cost equals marginal revenue the maximum should occur. At point a, the profit function will be decreasing to the left of a, since to the left of a marginal cost is greater than marginal revenue, implying that cost is increasing faster than revenue. Just to the right of a, similar reasoning shows is the cost is increasing more slowly than revenue and that the profit function will be increasing. If the profit function is decreasing to the left of a point and increasing to the right, then we have a relative minimum, not a relative maximum of that function.
At point b we can use the same reasoning to see that the profit function must be increasing just the left of b and decreasing just to the right. As a result the profit function must have a maximum at b.
The second graph below shows behavior of the cost and revenue functions. The marginal revenue function, which represents the rate of change or slope of the revenue graph, is constant so the revenue function must be linear, as indicated. The marginal cost function, which represents the rate of change of the cost function and therefore the slope of the graph of the cost function, starts with a relatively large value and decreases to a minimum between a and b; the cost function graph will therefore start with a relatively large slope which will decrease to a minimum, as indicated. The marginal cost function then increases, so that the graph of the cost function will get steeper and steeper, as indicated. Between points a and b, the slope of the cost function will be less than that of the revenue function. At point a the cost function exceeds the revenue function by a maximal amount and we have a maximum loss; at point b the revenue function exceeds the cost function by a maximal amount then we have a maximum profit.
.
`02
An example of a modeling situation is given below. The problem is to design a closed cylindrical can with the minimum possible surface area, in order to minimize the amount of material required to make the can.
As depicted below, we could build such a can with a diameter of approximately 18 cm and an altitude of 1 cm. You should verify that the volume of this can is approximately 1000 cm^3. Alternatively we might build a canned with the radius of approximately 3 cm and in altitude of 36 cm. You should verify that the volume of the scan is reasonably close to 1000 cm^3.
It is clear that the radius and height of the can determine its volume. So we began by finding the total area of the canned with radius r and height h.
The area of the can will be double the area `pi r^2 of the circle forming its top and bottom, plus the area of its sides, which will be equal to the product of the circumference 2 `pi r of the base and the altitude of the can. We therefore obtain the expression A = 2 `pi r^2 + 2 `pi r h.
We can't picked just any radius and height and build a can. We have to pick a radius and a height that gives it can a volume 1000 cm^3. Since the volume of the can is equal to the product of the area of its base edits altitude, we have V = `pi r^2 h = 1000.
So far the area function depends on both r and h. Since r and h are related to each other by the volume constraint, we can eliminate either variable from the area function. This is necessary before we minimize the area function; otherwise we will have two variables and when we take the derivative this will cause problems.
Your text solves a similar problem and at this point chooses to solve the volume relationship for the height h. This is probably the simpler way to proceed. But for the sake of contrast we will hear solve for r. We obtain r = `sqrt(1000 / `pi h), as shown below.
Substituting this expression for r into the area function we obtain area as a function of h only, as indicated in the last two lines of the figure below.
We now proceed to minimize the area function. We find the critical point by setting the derivative dA / dh equal to zero. The solution of the equation is straightforward and is shown below. It is clear that the derivative function goes from negative to positive at this value of h, since the only term depending on h is `sqrt(1000 `pi) h^(3/2) and is increasing.
Having obtained the height h = 10.8 cm of the can with minimum surface area, we substitute this value into our previous relationship r = `sqrt(1000 / (`pi h) ) to obtain approximately value r = 5.4 cm. You should check that these dimension indeed give us an area which is appropriately close to 1000 cm^2.
`04
Another modeling problem concerns the distance at which we can get the best view of the Statute of Liberty, given that its base is 46 m high-end that the total height of the statute including the base is 92 m. We define the best view as that for which the angle between our line of sight to the top of the base and our line of sight to the top of the statue is a maximum. Note that if we are too close to the base, this angle will be small, as it will be if we are far from the base. At some point between 'too close' and 'too far', the angle should be optimized.
We will find the angle as a function of our distance. We will use x for our distance from the statue, as indicated below.
The sketch shows us that at distance x, the angle between horizontal and the lower line of sight must be arctan(46/x), while the angle between horizontal and the upper line of sight is arctan(92 / x). The difference between these angles is therefore `theta = arctan(92/x) - arctan(46/x).
We will proceed to maximize this function.
Using the chain role in a straightforward manner we obtain the derivatives of the too inverse tangent functions. In the last step we factor out 46 / x^2 but still leave a complex fraction in the denominator of each term. We note that the x^2 in this term will multiply the denominator x^2 of the denominator of each complex fraction, leaving us
d`theta / dx = 46 ( -2 / (x^2 + 92^2) + 1 / (x^2 + 46^2) ).
Setting this equation equal to zero and dividing both sides by 46 we obtain the equation in the first line of the figure below. If we multiply both sides by the common denominator (x^2 + 92^2) (x^2 + 46^2), we obtain the equation in the second line which we proceed to solve. The result is x = 65. We conclude that the best to the Statue of Liberty is from a distance of 65 meters.
You can and should check situation out with your favorite flagpole. Try to get the best view of that portion of the top half of the pole. First walk up to the flagpole, crane your neck upwards and see what kind of view you have, then walk a couple of miles away from the flagpole and see what your view is like there. Then walk back toward the flagpole and determine at what distance the top half of the flagpole fills the greatest proportion of your vision.
Then measure the height of the flagpole by one means or another (e.g., by proportionality with the length of its shadow or by trigonometry). Then as a function of distance from the flagpole determine the function that models the angle `theta between the two lines of sight. Maximize this function and see how it compares with your perception.
As a final example we determine the dimensions of the rectangle whose area is A, and whose diagonal is a minimum.
If we let x be the width of such a rectangle we see that, since its length will be such that length * width = length * x = A, its length must be A / x. This information is depicted in the first sketch in the figure below.
In the second figure we see that the length of the diagonal is the hypotenuse of a right triangle whose legs are x and A/x. It follows from the Pythagorean theorem that L = `sqrt(x^2 + (A/x)^2 ).
To find the minimum length we find the critical points for this length function. We use the chain rule to find dL / dx, obtaining the expression in the last line of the figure below.
The critical points therefore occur at the values x which satisfy the equation in the top line of the figure below. We note that the second factor on the left-hand side consists only of positive quantities in most therefore be positive. Since this term is never zero we can divide both sides of equation by the term to obtain the much simpler equation 2x - 2A^2 / x^2 = 0. Multiplying both sides by x^3 we obtain the equation x x^2 - A ^ 2 = 0, which has positive solution x = `sqrt(A).
From this we determine that the length is A / x = A / `sqrt(A) = `sqrt(A), so that the rectangle with minimum diagonal has dimensions `sqrt(A) by `sqrt(A). That is, the rectangle is a square.
"