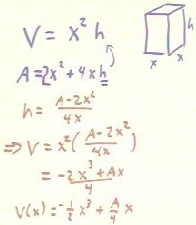
We begin by finding the volume of a closed box of the square base and a given area A.
Since the base of the box is square, we will use x for the length of the side of the base. We will call the height of the box h, so this volume will be V = x^2 h. Our constraint is that the total area of the box is A. The total area of the box will be double the area of the base plus four times the area of a vertical side, or A = 2 x^2 + 4 x h.
It is the volume wish to maximize, so we need to express the volume is a function of one variable. Solving the constraint A = 2x^2 + 4 x h for h we obtain h = (A - 2x^2) / (4x); we substitute this into the expression for the volume and simplified to obtain V = - 1/2 x^3 + A/4 x.
It is instructive to graph this volume function. We do so by graphing y = A/4 x, which will be a straight line through the origin with a slope of A / 4. The slope could be greater or less than that indicated in the graph below, depending on the value of the area A. We then graph y = - 1/2 x^3, and proceed to add the graphs of the two functions. At x = 0, both functions are zeros of the total volume will of course be zero. As x increases, the linear function is at first greater in magnitude than the cubic function, which has slope zero at x = 0. The volume function will therefore be positive, at least for time. However, the cubic function will eventually become equal in magnitude to the linear function and, since for positive x the functions have opposite signs, this sum will be again 0. The approximate point at which this happens is indicated on the graph by the purple arrows indicating the equal and opposite values.
The function V(x) will therefore have the approximate shape shown for the x values of interest (i.e., those values of x > 04 which the volume function is positive).
Now to maximize the function V(x), we find its critical point for x > 0. It is straight four to take a derivative, said it equal to zero and solve for x. We obtain x = +-`sqrt(A/6), and discard the negative value as meaningless for the present situation.
To find the volume corresponding to this critical point we simply substitute `sqrt(A/6) for x in our expression for the volume V(x).
Next we derive Snell's Law v1 / v2 = sin(`theta1) / sin(`theta2) by minimizing the time required for a ray of light to move from point A to point B, as depicted in the figure below. We assume that A lies a distance a from a plane interface between two materials, that B lies at a distance b from the interface on the other side, that the distance from A to B in the direction parallel to the interface is c, and that the velocity of light on the A side of the interface is v1 while the velocity is v2 on the B side.
We are told that light behaves much like a good lifeguard in the lifeguard problem, traveling any straight line to a point on the interface then in a straight line to B and choosing the position at which it reaches the interface in such a way that the total time for point A to point B is minimized. The parameters `theta1 and `theta2 are the angles made by the ray in the two materials with the dotted line perpendicular to the interface.
If we let x stand for the distance to the 'left' of the point B at which the ray reaches the interface, then we see that the distance traveled from A to this point will be the hypotenuse of a right triangle whose legs are a and c-x, or `sqrt(a^2 + (c-x)^2). The distance from the interface to B is similarly found to be `sqrt(x^2 + b^2).
The time required to move from point A to point B will therefore be T(x) = dist from A to interface / v1 + distance from B to interface / v2 = `sqrt(a^2 + (c-x)^2) / v1 + `sqrt(x^2 + b^2) / v2. It is straightforward to take the derivative of this function to obtain T'(x) as shown in the last line of the figure below. The denominators, which might not be very legible, are 2 `sqrt(a^2 + (c-x)^2) v1 and 2 `sqrt(x^2 + b^2) v2.
We find a critical point by setting this expression equal to 0. We first note that each numerator and each denominator contains a factor 2, so that these factors can be divided out. We then multiply by the common denominator to obtain the third line in the figure below, and then move the second term to the right-hand side of the equation. At this point we squared both sides of the equation, with the idea that some terms will cancel from the mess we obtain. In retrospect this was a bad idea, since it is point we essentially had the solution, but we were caught up in the algebra and failed to notice where we were.
Before going on we will point out that we were to show that v1 / v2 = sin(`theta1) / sin(`theta2), and it might have been a good idea to put the equation in the form v1 / v2 = whatever comes out. In that case we would have noticed that what comes out is v1 / v2 = - (x / `sqrt(x^2 + b^2) * `sqrt(a^2 + (c-x)^2 ) / (x-c) = (x / `sqrt(x^2 + b^2) * `sqrt(a^2 + (c-x)^2 ) / (c - x). This might not look like much, but a quick look at the original figure shows us that (x / `sqrt(x^2 + b^2) is just sin(`theta1), while `sqrt(a^2 + (c-x)^2 ) / (x-c) can be converted to give us (x - c) / `sqrt(a^2 + (c-x)^2 ) = sin(`theta2). Thus the right-hand side is just sin(`theta1) / sin(`theta2), and we have proven our result.
Additional note: The very first equation in the figure below has the result. This equation can be rewritten -sin(`theta1) / v1 + sin(`theta2) / v2 = 0. This can easily be rearranged to give the desired result.
Proceeding to unnecessarily square both sides of the equation, then to distribute some of the multiplications until we realize that nothing much is going to cancel out, we then say that we can substitute and expression for v1 in terms of v2, c, x and b and that the whole thing will probably work out. Except that the denominator (b/x) of this expression should read x / `sqrt(x^2 + b^2), this would probably work out.
Students using the CD's will undoubtedly be entertained when we then proceed to return to the squared equation to observe the existence of the expressions for the squared sines of `theta1 and `theta2, and to finally draw the correct conclusion to this exercise. This is an excellent example of how even an experienced can lose sight of the forest for the trees.
We now proceed to define the hyperbolic cosine and hyperbolic sine functions. The definitions are as depicted below.
It is straightforward to show that the derivative of the hyperbolic cosine function is (e^x - e^-x) / 2, which is equal to the hyperbolic sine function. Similarly the derivative of the hyperbolic sine is equal to the hyperbolic cosine. These relationships are much like those for the trigonometric sine and cosine functions, except that we don't get a - sign for the derivative of the hyperbolic cosine.
We define the hyperbolic tension in the obvious way and can easily show that its derivative is the reciprocal of the square of the hyperbolic cosine, which is directly analogous to the situation for the trigonometric tangent function.
Graphs of the hyperbolic sine and cosine function are easily obtained by first graphing the functions e^-x / 2 and e^x / 2, as well as -e^x / 2. To obtain the hyperbolic cosine function we add the first two of these functions. As we move away from the y axis, one or the other of these functions will rapidly approach zero so that the graph rapidly approaches that of the other function. And x = 0, the some of the two functions approaches 1/2 + 1/2 = 1. The hyperbolic cosine function is therefore symmetric about the next axis, with a shape. Near the one depicted on the graph.
To graph hyperbolic sine function we add e^x / 2 to e^-x / 2. Again, away from the y axis one or the other of these functions will approach 0 and graph will be close to the function which does not approach zero. As we approach the y axis, the functions become nearly equal and opposite and we approach y = 0, as depicted below.
We also note that the identity cosh^2 x - sinh^2 x = 1 is easily proved. This identity is analogous to the identity cos^2 x + sin^2 x = 14 trigonometric functions. It is almost as if we took the - sign that we might have expected for the derivative of the cosine function and placed it into this identity.
Hyperbolic functions are important in a number of areas, as mentioned in your text.
"