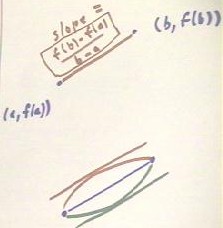
The Mean Value Theorem can be illustrated by a simple exercise. Sketch two points, representing points (a, f(a)) and (b, f(b)) of the graph of some function f(t). Your points need not be positioned like those in the figure below; just don't make one point directly above or below the other. Connect the points with a straight line.
Now sketch a continuous smooth curve from one point to the other. It can be any sort of a curve, as long as it is smooth and as long as you keep moving from left to right.
Now find a point on your curve where the tangent line to the curve is parallel to the straight line you drew between the points. If you have followed directions, there must be such a point. If not, send me the picture right away and I'll make you famous. I promise. I'll give you all the credit. Believe me . . . .
Most people draw a curve like that suggested by either the red or the green curve at the bottom of the figure above. Plausible tangent lines are shown for each.
Now try to get creative and make a curve that will make me .. I mean you ... famous or infamous, as the case may be. Try to draw a curve, according to directions, that has no point where the tangent line is parallel to the straight line.
You will soon conclude that it can't be done. You might even think that your inability to do it proves that it can't be done, or that your experience shows you beyond a shadow of a doubt that it can't.
Well, no offense, but no mathematician is going to think that just because you can't do it, it can't be done. We don't even believe such things about ourselves or each other; we sure aren't gonna believe it about you. We want proof, not claims of omniscience from mere mortals. And just because you are convinced by your intuition and experience, don't think that we will accept your word for it. You have to show us, logically and beyond a shadow of a doubt, that it can't be done. Again, no offense. We hold ourselves and each other to the same standards.
It turns out that we can prove that any smooth and continuous curve -- that is, any curve which has a derivative at every point -- that goes from (a, f(a) ) to (b, f(b) ) must have a point where the derivative is equal to the slope of the line segment between the points. This is equivalent to saying that every such curve past have a point where the tangent line is parallel to the line between the points.
We state this formally as the Mean Value Theorem.
Mean Value Theorem: If the function f(x) is differentiable on the interval [a, b], then there exists a value c, with a < c < b, such that the derivative f'(c) is equal to ( f(b) - f(a) ) / (b - a).
We of course recognize ( f(b) - f(a) ) / (b - a) as the slope of the line segment between the two points (a, f(a) ) and (b, f(b) ).
We are not going to prove the Mean Value Theorem here. The proof is constructed in a series of two exercises in your text, and these exercises have been assigned. Instead we're going to look at the couple of important theorems that can be prove relatively easily using the Mean Value Theorem.
This theorem can be proved fairly easily using the Mean Value Theorem. Suppose that a function f(x) satisfies the conditions of the Theorem, with f'(x) > 0 for all x in interval [a, b]. Suppose now that, contrary to what we are trying to prove, there exists a pair of points x1 and x2 in [a, b] with the property that x1 < x2, but f(x1) > = f(x2). Then the slope of the line segment from (x1, f(x1) ) to (x2, f(x2)) must not be positive. But by the Mean Value Theorem, there must therefore exist a point c between x1 and x2 where the derivative is equal to the slope of this line segment, and is therefore not positive. But this contradicts the assumed condition that f'(x) > 0 for every x between a and b. Our only conclusion is that there can be no such pair of points x1 and x2, so that whenever x1 < x2, f(x1) must be < f(x2).
We can also use the Mean Value Theorem to prove the Racetrack Principle. This Theorem essentially says that if two functions f(t) and g(t) begin at the same t with the same values, then if one of them has a derivative that is always larger than the other, it immediately becomes larger than the other and stays that way.
This seems obvious if we consider the fact that the graphs of the two functions both start at the same point, and since one of the functions always has a larger derivative, its graph always has the greater slope, its values will immediately become, and will always be greater than those of the other.
We can also use the Mean Value Theorem to prove the Racetrack Principle. This Theorem essentially says that if two functions f(t) and g(t) begin at the same t with the same values, then if one of them has a derivative that is always larger than the other, it immediately becomes larger than the other and stays that way.
This seems obvious if we consider the fact that the graphs of the two functions both start at the same point, and since one of the functions always has a larger derivative, its graph always has the greater slope, its values will immediately become, and will always be greater than those of the other.
We state the precise conditions for this situation. We assume that we have to functions f(x) and g(x) which are continuous on some closed interval [ a, b ], which are differentiable on (a, b) (note that differentiability at the end points of the interval is not necessary), and for which f(a) = g(a). Then the Theorem states that if f'(x) < g'(x) for all values of x in the interval (a,b), it follows that f(x) < g(x) for all values of x in (a,b).
The proof of this Theorem using the Mean Value Theorem is not too difficult. We begin by defining the difference function h(x) = g(x) - f(x). The derivative of h(x) is just g'(x) - f'(x). Since g'(x) > f'(x) for all values of x in the interval (a, b), then by the Increasing Function Theorem we see that the difference function h(x) = g(x) - f(x) must be increasing on the interval. Since h(a) = g(a) - f(a) = 0, it immediately follows that h(x) > 0 for all values of x on the interval. Hence g(x) - f(x) > 0 and g(x) > f(x) for all values of x on the interval.
"