The Fundamental Theorem of Calculus
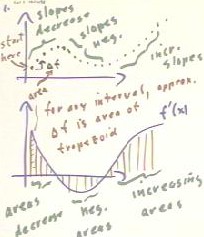
1. From the graph of f'(x), how could reconstruct an approximate graph of f(x)?
We begin with lower of the two graphs in the figure below. This graph represents the derivative function f'(x).
The derivative function f'(x) represents the rate at which the function f(x) is changing with respect to x. It follows that the area under this graph, between two x values, corresponds to the change in f(x) between those x values.
Consider the first interval of the f' graph. It has some positive area, which means that the graph of f(x) must increase over the same x interval by an amount equal to this area. That is we have a `df equal to the area under the first 'sliver' of the f'(x) graph.
This `df will be added to the original value of the function f(x) at the first x value. This original value can be anything at all, but once specified the function f(x) will be 'built' on this value. We assume the value corresponding to the point labeled 'start here' on the top graph. From this point we add the value `df obtained from the area under the f' graph, and assign this value to the new x value (the x value of the right-hand endpoint of the first interval).
On the second interval of the f' graph we see that the area is slightly less than that of the first. Thus the corresponding `df on the f(x) graph will be slightly less. As a result we see the slope of the f(x) graph beginning to decrease. This will continue as we add the `df values corresponding to the next few intervals, on which the area continues to decrease.
Thus on the region of the f'(x) graph labeled 'areas decrease', the `df values on the f(x) graph, and therefore the slopes, of the f(x) graphs decrease, as indicated.
The areas under the f' graph now decrease into negative values, which will correspond to negative `df values and therefore negative slopes, as indicated on both graphs. We note that the negative values get greater and greater in magnitude, reach a maximum magnitude then decrease in magnitude. This corresponds to the slopes of the f(x) graph, which become more and more negative, then while remaining negative become less and less so; the concavity of the f(x) graph therefore changes from negative to positive at the point for the f'(x) graph reaches its minimum.
The areas under the f'(x) graph than return to increasing positive values, corresponding to an increasing positive slope for the f(x) graph.
2. If r(t) is the rate of depth change vs. clock time function, then what is the depth vs. clock time function?
The function which models the rate of depth change is the derivative of the depth function with respect to clock time. That is, if y(t) is the depth function, then y'(t) = r(t) is the rate of depth change function.
It follows that y(t) is an antiderivative of r(t).
3. If depth changes at a rate given by r(t) = 10 e^(-.02 t), then by how much does the depth change between clock times t = 3 and t = 10?
The function which models the rate of depth change is the derivative of the depth function with respect to clock time. That is, if y(t) is the depth function, then y'(t) = r(t) is the rate of depth change function.
It follows that y(t) is an antiderivative of r(t).
Since we know that the depth function y(t) is an antiderivative of the rate change function y'(t) = r(t), the Fundamental Theorem of Calculus tells us that the change in the depth function between two clock times is the integral of the rate function between those times. Thus we have the integral in the second line below.
We note, as circled in green, that this integral is equal to the difference in the values of the antiderivative function between the endpoints of the interval over which we integrate.
In the third line in the figure below we use the property of the integral which allows us to 'factor out' the constant factor 10.
We now need only find an antiderivative of the function e^(-.02 t) and apply the Fundamental Theorem.
If we were to try e^(-.02 t) as our antiderivative, then since the derivative of this function is -.02 e^(-.02 t), which isn't quite the e^(-.02 t) we want. However, if we multiply by -50, we do get what we want. So our antiderivative will be -50 e^(-.02 t). You should take this derivative and see for sure that it gives us e^(-.02 t).
We therefore apply the fundamental Theorem with F(t) = -50 e^(-.02 t), obtaining the expression in the fourth line. We evaluate this expression and obtain the desired depth change.
4. If depth changes at a rate given by r(t) = 2t + 1 - 1/(t+1), and if depth that clock time t = 0 is 100, what is the depth function y(t)?
This problem is similar to the previous. See the figure below #5.
The Chain Rule
5. Use the chain rule in both the f(g(x)) and df / dx forms to find the derivative of y = e^(x^2).
The solution is in the figure below.
6. Use the chain rule to determine the derivative of the function y = x^.2 as the derivative of an inverse function.
This technique may be reviewed in Class Notes or in the text. The steps are outlined below. We let g9x) be the function whose derivative we wish to find and f(x) the inverse function. Then f(g(x)) = 2 and (f(g(x)) ' = 1. From the chain rule we find another expression for (f(g(x)) ' and set it equal to 1. We then solve for g'9x).
7. Use the chain rule to determine the derivative of the function y = arcsin(x) as the derivative of an inverse function.
****
8. At clock time t, the front end of a railroad train on a straight track is at distance 100 - 20 t meters from a crossing. An automobile is sitting on the road, which makes a right angle with the tracks, and the driver is 30 meters from the tracks in the driver's seat. At clock time t, what is the distance z from the front of the train to the driver? At clock time t, at what rate is the distance between train and driver changing with respect to time?
Derivatives of Sine and Exponential Functions
9. Using the definition of the derivative and the fact that for x close to 1, e^x is close to 1+x, derive the expression for the derivative of e^x.
The steps are shown below, and may be reviewed in the text and in the class notes.
10. Using the derivatives of the sine and cosine functions, show that d / dx (tan x) = 1 / cos^2(x).
Tangent line approximation
11. Give the expression for the tangent line approximation to the function y = f(x) at the point (a, f(a)), and support your expression with a sketch of the situation in the neighborhood of this point, accompanied by a clear explanation.
12. If f(3) = 7 and f'(3) = .5, then what is the approximate value of f(3.1)?
This is really a simple problem, once you see that we are given the value of a function and its derivative at a point, which is all we need to find the equation of the tangent line. We can then of course use the tangent line to find the desired approximate value. Before you see this, of course, the problem is incomprehensible.
The equation of the tangent line is therefore f(x) = f(3) + f'(3) (x-3) = 7 + .5 (x-3), and is expected to be a good approximation of f(x) near x = 3.
Evaluating the tangent approximation at x = 3.1, we obtain f(x) = 7.05.
13. Write out the tangent line approximation to y = x^2 near the point (2,4), then write out the expression for the error of the tangent line approximation at a point (x, y) on the graph of y = x^2 at a point near x = 2. Evaluate this expression at x = 2.2, 2.4 and 2.6, and sketch a graph of the error between x = 2 and x = 3.
To obtain the tangent line approximation we need the values of the function and its derivative at the desired point. It is very easy to see that for this function, f(2) = 4 and f'(2) = 4. The tangent line approximation is therefore f(x) = 4 + 4 (x-2) = 4x - 4.
The resulting error in the approximation is x^2 - (4x - 4) = x^2 - 4x + 4. This function factors into (x - 2) ^ 2, which has a graph which is a parabola with vertex at (2,0). Thus, as x gets close to 2, the error approaches 0 as indicated by the graph of this parabola.
14. Write out the tangent line approximation to y = x^2 near the point (2,4), then write out the expression for the error of the tangent line approximation at a point (x, y) on the graph of y = x^2 at a point near x = 2. Call this error function E(x). Determine the limiting value of E(x) / (x-2), as x approaches 2.
As seen in the previous problem, the error function is E(x) = x^2 - 4x + 4 (erroneously written x^2 - 4x - 4 in the figure below). Thus we have E(x) / (x-2) = (x^2 - 4x + 4) / (x-2). We take the limit of this expression (again written erroneously was a -4 instead of a +4), as in the third line below. We note that this expression (if written correctly with the +4) is at this point of the form 0 / 0, and that we could and should evaluate the derivative using l'Hopital's Rule. Instead we factor the numerator and divide out the x-2 common to both numerator and denominator, obtaining an expression which apparently has a limit of 0.In any event, we see that not only does the error term E(x) approaches zero as x approaches 2, but even the ratio E(x) / (x-2) approaches 0 at this limiting x value. We conclude that the error term approaches zero faster than x approaches 2, and that our approximation gets better and better faster and faster as we approach x = 2.
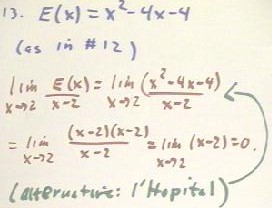
Proof of product rule
15. Explain the proof given in the text of the product rule.
The essence of the proof is in the sketch below, where g(x) and f(x) are represented by the length and width of the black rectangle in the figure below, and f(x+`dx) and g(x+`dx) as the width and length of the 'red' rectangle, which includes the black rectangle. The difference f(x+`dx) g(x+`dx) - f(x) g(x) encountered in the numerator of the difference quotient for the f(x) g(x) function is therefore represented by the difference between the area of the smaller and the larger rectangles in the figure as drawn. Most of this area is in the green shaded regions, which have areas g(x) * ( f(x+`dx) - f(x) ) and f(x) * ( g(x+`dx) - g(x) ), and in the rectangle labeled 'small'. As `dx -> 0, the 'green' areas also approach 0, and the 'small' region approaches 0 even faster.
When these approximations are substituted into the difference quotient, the resulting expression has a limit that gives us the product rule.
16. Use a tangent-line approximation to prove the product rule.
When the tangent-line approximation f(x+`dx) = f(x) + f'(x) * `dx to f(x+`dx), in the similar approximation for g(x+`dx), are substituted into the difference quotient for the product function f(x) g(x), we obtain an expression whose limit gives us the product rule. See class notes for the details.
Implicit differentiation
17. Using x = 2, determine the value of y given implicitly by the equation x^2 y^2 - x^3 y - x = 0. Repeat for x = 2.2. Sketch the corresponding points on the graph of y vs. x, and determine the slope of the line segment between these points. Then using implicit differentiation determine y' as a function of x and y. Evaluate this expression at the x = 2 point you have determined and compare it with the slope you found. Why should the two values be close? Why should they not be exactly the same?
When we substitute a value of x into the equation we obtain a quadratic equation for y, which we easily solve to obtain to y values. We can pick either y value. Suppose we pick the one corresponding to the + of the +- in the quadratic formula. Then we make the same choice when determining the y values for x = 2 and x = 2.2. This gives us two values of y, as indicated below, and hence two (x,y) points on a graph of y vs. x. You should calculate these values for yourself.
We can then determine the difference `dy of the two y values, and hence the approximation `dy / `dx to the slope of the graph, using `dx = 2.2 - 2 = .2.
We can then implicitly differentiate our y function, using the usual procedures to obtain an expression for y' in terms of x and y. We can evaluate this expression at the x = 2 point, using x = 2 and the corresponding y value.
Our result should be close to the average derivative `dy / `dx calculated previously. We could also compare this average derivative to the y' obtain that the x = 2.2 point, or to the average of the two y' values obtained at the x = 2 and x = 2.2 points. You should do this and look carefully at how close the various results are to the original approximation.
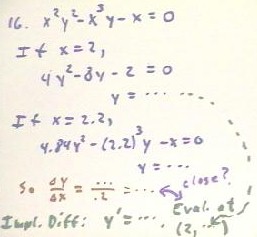
Marginality
18. Explain in common-sense terms why maximum profit should occur where the slopes of the revenue and cost functions are equal, and why at that point we should have a negative derivative for the function marginal revenue - marginal cost.
If revenue is increasing faster than cost, we can make a greater profit by producing more. If revenue is increasing more slowly than cost, we will make a greater profit by producing less. Only if revenue and cost are increasing at the same rate, so that R' = C', or MR = MC, will we be making the maximum profit.
However, if the derivative R' - C' of our profit function is increasing when R' = C', we will have a minimum of the profit function rather than the maximum we are seeking (this is because a function is maximized at a critical point when its derivative is decreasing). Therefore we seek a point where R' = C', giving us a critical point of our profit function R - C, and where R' - C' is decreasing.
19. Explain in common-sense terms why, if marginal cost is less than marginal revenue, profit would increase with slightly increased production.
This explanation and the other two in this section follow from the same concepts as those outlined in the preceding problem.
20. Explain in common-sense terms why, if marginal cost is greater than marginal revenue, profit would increase with slightly decreased production.
21. Explain in common-sense terms whether, if marginal cost and marginal revenue are equal and the rate of increase of marginal cost is greater than the rate of increase of marginal revenue, we have a maximum or a minimum in our profit function.
Modeling
22. Explain how to solve the lifeguard problem.
For the complete solution of the lifeguard problem, see the text and the class notes.
An outline of the solution follows:
We begin by finding the distance from the lifeguard to the water, assuming that the lifeguard enters the water and position x, and the distance from this point to the swimmer, using the Pythagorean Theorem.
We then proceed to find a total time required for the lifeguard to reach the swimmer, noting that the total time is distance1 / v1 + distance2 / v2. This total time will be a function T(x) of x.
We then proceed to minimize the function T(x).
The algebra is not trivial, but it is not too complicated.23. Explain how to solve the problem of minimizing the area of a closed cylindrical can for a given volume.
Outline (see text and class notes for details):
We minimize the area of a closed cylindrical can by expressing the volume and area of the can as functions of the radius r of the base and the altitude h of the can.
Since the volume is taken as a fixed given quantity, we solve the volume constraint equation for either x or h. We then substitute this variable into the expression for the area A, obtaining area as a function of that variable.
We then minimize A has a function of the variable.
Having obtain the value of the variable which minimizes A, we substitute this variable back into the volume constraint equation and obtain the value of the other variable, thereby obtaining the dimensions of the desired can.
24. Explain how to solve the problem of maximizing the volume of a closed rectangular box for a given surface area.
25. What is the minimum total cost of enclosing a 5000 square foot rectangular area, if three sides are to be enclosed with fencing costing $25 per foot and the remaining side with fencing which costs $10 per foot?
Pendulum
26. If the period of a pendulum is given by T = 2 `pi / `omega, where `omega = `sqrt( 980 / L ), then without actually computing the period determine the approximate change to be expected in the period if L is changed from 120 to 130. Verify your calculation by now computing the period at the two lengths and determining the actual difference. What is the percent error of the approximation, expressed as a percent of the actual change?
We outline the solution to this problem. See class notes for details.
We begin by substituting the expression for `omega into the expression for period T, obtaining T as a function of L, as shown in the figure below.
We then note that near a given value of L, the difference `dT corresponding to a difference `dL in length will be approximately equal to the product of the derivative dT / dL and the length difference `dL.
In calculating `dT, we must be careful to evaluate dT / dL at an appropriate value of L -- that is, at a value close to the lengths involved in the situation.
27. If the frequency of a pendulum is given by f = `omega / (2 `pi), where `omega = `sqrt(980 / L), then will not actually computing the frequency determine the approximate change to be expected in the frequency if the length L is changed from 80 to 90. Verify your calculation by now computing the frequency at the two lengths in determining the actual difference. What is the percent error of the approximation, expressed as a percent of the actual change?
The solution to this problem is very similar to that of the preceding problem. The function in this case is f(L) = `sqrt(980/L) / (2 `pi). After calculating the derivative df / dL, we approximate `df by df / dL * `dL, evaluating df / dL had inappropriate value of L.`epsilon, `delta
28. On the graph of y = x^2, what `delta is sufficient to squeeze y within `epsilon of y = a^2?
The figure below shows how y = x^2 will lie between a^2 - `e and a^2 + `e whenever x lies between `sqrt(a^2 - `e) and `sqrt(a^2 + `e). If we choose `delta such that a - `delta and a + `delta lie between these x values, then we will have squeezed y between the desired values.
Recalling that `sqrt(1 +- small number) can be approximated by 1 +- 1/2 (small number), we see that `sqrt(a^2 + `e) = a `sqrt( 1 + `e / a^2), which is approximately equal to a (1 +- 1/2 `e / a^2) = a +- 1/2 `e / a. So it is nearly safe to say that for small values of `e, whenever x is within 1/2 `e / a of a, x^2 will be within `e of a^2. To be really safe, we can restrict x just a little more, and say that for small enough values of `e, we will be within the desired ranged as long as x is within `delta = 1/4 `e / a of a.
So we select `delta = 1/4 `e / a and say that whenever x is within `delta of a, x^2 is within `e of a^2.
29. On the graph of y = 1/x, what `delta is sufficient to squeeze y within `epsilon of y = 1/a?
In the figure below we show how 1/x will be within `e of 1/a has long as x lies between 1 / (1/a + `e) = a / (1 + `e a) and 1 / (1/a - `e) = a / (1 - `e a). Using the approximation that 1 / (1 +- small number) is approximately equal to 1 -+ small number, we can see (see second figure below) that this interval is nearly the same as the interval from a (1 - `e a) = a - `e a^2 to a (1 + `e a) = a + `e a^2. To be safe we choose `delta = `e a^2 / 2. Then we can be sure that for small enough `e, whenever x lies between a - `delta and a + `delta, 1/a lies between 1/a - `e and 1/a + `e.
Theorems important to the foundations of the calculus
30. State the Extreme Value Theorem and outline its proof, showing clearly how the Nested Interval Theorem is necessary for the proof.
31. State the Mean Value Theorem and use it to prove the Increasing Function Theorem.
32. State the Nested Interval Theorem and completeness axiom.
33. State the Racetrack Principle Theorem and prove it from the Increasing Function Theorem.
"