Quiz Problems
Some basic function behaviors include increasing in decreasing behavior, and the behavior of the rates at which the function increases and/or decreases. The quiz problems for today asked for the signs of f' and f'' for functions which were increasing an increasing rate, increasing at a decreasing rate, decreasing at an increasing rate, and decreasing at a decreasing rate.
If a function is increasing, then the slope of its graph is positive, whether its rate of increase is increasing or decreasing. Therefore any increasing function has a positive slope. It follows that if f is an increasing function, f' must be positive.
Similarly if a function is decreasing, the slope of its graph is negative, whether it's rate of decrease is increasing or decreasing. Therefore any decreasing function has a negative slope. Thus if f is a decreasing function, f' must be negative.
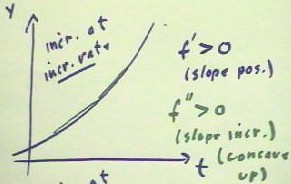
If a function is increasing at an increasing rate, then its graph looks like the one below, increasing from left to right with an increasing slope. Since the slope increases from point to point, f' increases from point to point, so the rate which f' changes is positive. Since f'' is the rate of which f' changes, f'' will be positive.
A more detailed and rigorous argument is the following: Whenever`dt is positive (representing two values of t with the second greater than, or to the right of, the first) it follows that the difference `df' between the two values of f' will be positive and `df' / `dt will be positive. In the limit as `dt -> 0, `df' / `dt will remain positive, so that f'' must be positive.
We note also that the graph of this function is is concave up. These ideas are summarized in the figure below.
If a function increases at a decreasing rate, then its slope will decrease from point to point and the graph will look like the one below, increasing from left a right but in a matter which makes the graph concave downward. Since the slope f' is decreasing the rate f'' which the slope changes will be negative. (More rigorously, if `dt is positive corresponding change `df' in the rate f' will be negative so that `df ' / `dt will always be negative and its limit `df' / `dt = f'' will always be negative).
A function f(t) which decreases at an increasing rate will get lower and lower as t increases, and will do so faster and faster. Note that 'increasing rate' in the phrase 'decreases at an increasing rate' refers to the decrease, which therefore must get faster and faster. This gives us a graph with the shape shown below. Note that this graph is concave downward.
Since the graph is always sloping downward, f' must be less than 0. Since the slope is always decreasing (an increasingly negative slope takes negative values of greater and greater magnitude, and so is decreasing), the rate f'' which the slope f' changes must be negative.
If a function is decreasing at a decreasing rate, its decrease must get more and more gradual. Hence f' must take negative values of smaller and smaller magnitude, and its values are therefore increasing. It follows that the rate f'' at which f' changes must be positive. We note also that the graph must be concave upward. The figure below shows such a function.
Text Problems
One text problem provided a table of values of f(x) vs. x and requested estimates of f' and f'' at various points. We might consider the table of f(x) vs. x below as an example of this sort of problem. Suppose that the problem requested the approximate value of f' at x = 3.3, and at x = 3, and the value of f'' at x = 4.
It is unnecessary to calculate all possible estimates of f' and f'', but to show the general procedure we will calculate f' over each interval and f'' over each midpoint-to-midpoint interval.
We begin by calculating the midpoint of each x interval. We place these midpoints in the third column. Then for each interval we calculate `df / `dx. For example on the first interval x runs from 2 to 2.7, for which the midpoint is 2.35. The run on this interval is `dx = .7, and the rise is `df = 9-5 = 4, so the rate (or slope) `df / `dx is `df / `dx = 9/5 = 5.7. This is an approximation to f' over the interval, and on first approximation will be associated with the midpoint of the interval, so we might say that f'(xMid) = f'(2.35) = 5.7 (approximately).
Having obtained a table for f'(xMid) vs. xMid, we proceed to obtain a table for the average rates at which f' changes over these xMid to xMid intervals. We will obtain for each xMid to xMid interval a midpoint between the xMid values, which we will call xMidMid. Note that these values very nearly coincide with original x values (the second xMidMid value should read 3.33, not 2.33); they would exactly coincide if the x intervals were of uniform length.
Between xMid = 2.35 and xMid = 3.0, xMid changes by `dx = .65 and the approximate value of f' changes by `df' = 5.0 - 5.7 = -.7. The average rate of which f' changes is therefore `df' / `dx = -.7 / .65 = -1.1. This value will be associated with the x value halfway between xMid = 2.35 and xMid = 3.0; we call this value xMidMid = 2.68 and thus we say that f''(2.68) = -1.1 (approximately; note that this approximation is based on an approximation of f', and hence is in approximation of approximation. As such it is regarded as less accurate than the approximations of f'.).
To estimate the value of f' at x = 3.0, we need only note that 3.0 is the midpoint between x = 2.7 and x = 3.3. So the average value of f' on the interval between these two x values will be associated with this midpoint. We thus see that f'(3) = 5.0 (approx).
To estimate the value of f' at x = 3.3, we first note that 3.3 has the interval from 2.7 to 3.3, with its average rate of 5.0, to its left and interval from 3.3 to 4.0, with its average rate of 2.9, to its right. It therefore makes a certain amount of sense to associate the average of these two rates with the point 3.3, and therefore to say that the approximate derivative f' at x = 3.3 must be the average (5.0 + 2.9) / 2 = 3.95 of the two rates. This is not a precise value, because clearly the rate which the rates are changing keeps changing, and also because the x interval to the left in the interval to the right are not of exactly equal lengths.
Our estimate of f'' at x = 4 (which, as the table shows, is -6.1) takes advantage of the fact that 4.0 is the boundary between two x intervals of equal length. On the interval from x = 3.3 to x = 4, the average value of f' is 2.9; on the interval from x = 4 to x = 4.7 the average rate is f' = -1.4. From the midpoint of the first interval to the midpoint of the second we have `dx = .7; the change in f' is `df' = -1.4 - 2.9 = - 4.3, so our approximation of f'' is f'' = `df' / `dx = -4.3 / .7 = -6.1.
A trapezoidal graph of this data makes these ideas clearer. The graph below shows the x values from the table above and, expressed as altitudes of the trapezoids, the values of f associated with each x value. The average rate of change for each interval is the slope f' associated with the trapezoid, and is found by dividing the rise `df by the run `dx. Each average rate is associated, in our first approximation, with the midpoint of the corresponding interval.
The average rates at which the rates change will be found by dividing the change in rate `df at the x value between each pair of trapezoids by the distance between the midpoints of those trapezoids (since the average rates are associated with the midpoints). For example at x = 2.7, the slope changes from 5.7 (associated with the midpoint x = 2.35) to 5.0 (associated with the midpoint x = 3.0). We thus have `df' = slope change = -.7, and `dx = 3.0 - 2.35 = .65, so that f'' = `df' / `dx = -.7 / .65 = -1.1. This is our 'rate of slope change', designated by <-1.1> directly above x = 2.7. These rates of slope change are thus associated with the second derivative f''.
Using standard methods for calculating rates of slope change, we also obtain the slope change rates <-3.1> and <-6.1> associated with x = 3.3 and x = 4.0, respectively. Note that these rates agree with those found in the table.
Another text problem concerned the graph shown below of y = f'(x) vs. x. This is the graph of the derivative f', not a graph of the function f. Several questions are asked about the function f, its derivative f' and its second derivative f''.
One question asked which of the specified x values x1, x2, ..., x6 gives us the greatest value of f'(x). Since the graph shows the values of f'(x) vs. x, we simply determine which designated x value gives us the greatest value of y = f'. This clearly occurs at x = x3, among the specified points.
Another question asked which of the specified x values gives us the greatest value of the function f. If we try to visualize the graph of f(x), we see from the graph of f'(x) that since f' is always positive, the slope of the f(x) graph will always be positive and f(x) will always be increasing. Sometimes is increasing at a faster rate (e.g., at x = x3) and sometimes a slower rate (e.g., at x = x2 or x = x5). About it is always increasing. Therefore its value will be greater at greater x values and the greatest value (among the designated points) will be taken at x = x6.
Still another question requested the designated point at which f'' takes its maximum value. Since f'' is the derivative of f', which is represented by the slope of the graph of f', we simply find the designated point at which the graph of f' is a maximum. Since the slope of the graph is positive that only one of the designated points, x = x6, it is at this point that f'' takes its maximum value.
Another text problem gave the velocity function v = 1 / (1+t) of a turtle, in meters/minute, as the function of the clock time t, with t measured in minutes. We were asked to find the total distance traveled by the turtle during the minute between clock times t = 0 and t = 1, using `dt = .2.
Our best approximation would be obtained by first evaluating the velocity at t = 0, .2, .4, .6, .8 and 1. We obtain the velocities shown in the table below. We can then determine the average velocity (designated by the v with the bar over the top, which will be referred to as vBar) for each interval. For example on the first interval, from t = 0 to t = .2, the average of the velocities is the average of the associated velocities v = 1 and v = .83; this average is .92. The remaining values of vBar are shown in the table.
For each interval, the distance `ds moved by the turtle will be the product of the average velocity (in meters/minute) and the .2-minute duration of the interval. So on the first interval, for example, we obtain `ds = .92 meters / minute * .2 minute = .18 meters. This value is shown in the `ds column. The remaining values of `ds are shown on the table. The total of these `ds values is `dsTot = .69 meters.
These estimates are best visualized by a graph such as the one below. We see the t values from the table represented along the t taxes and the velocities represented as altitudes of trapezoids. On each interval, we use the lower of the two velocities to obtain the lower estimate of the distance over that interval. For example on the first interval, we have to velocities v = 1 and v = .83. The lower of these velocities is v = .83, and we will use this as a basis for determining the approximate distance moved between t = 0 and t = .2. The resulting distance will be the product of the velocity .83 meters / minute and the time duration .2 minutes, or .83 * .2 = .17 (incorrectly labeled as .16 below). This calculation corresponds to the area on the first interval beneath the horizontal red line corresponding to the altitude .83.
The velocities and resulting `ds estimates are shown in red as the 'Lower' values. We see that our lower estimate of the total distance `dsTot is approximately .64.
The upper estimates will use the greater of the velocities for each interval, and will correspond to the areas beneath the green horizontal lines on the graph. These values are given in green below. We note that are upper estimate of the distance is `dsTot = .74.
If we look at the upper and lower `ds estimates for the five intervals, we see that the first four lower estimates coincide with the last four upper estimates, so that when the lower estimate is subtracted from the upper these four values will cancel. We will be left with only the difference of the first upper estimate and the last lower estimate, so that the difference will be .2 - .1 = .1. This is consistent with the difference between our lower and upper estimates of `dsTot.
We note three things. First, if we had used a smaller `dt, each of the `ds estimates would have been smaller and the difference between the first upper estimate and the last lower estimate would have therefore been smaller. Since this difference is the difference between the lower and upper estimate, we see that this difference will shrink as the interval `dt shrinks.
The second thing we note is that the difference between the upper and lower estimates corresponds to the total area of the 'red-green' boxes at the top of each trapezoid. Each of these boxes represents the difference between the lower and the upper estimate of the area, so clearly there total represents the total difference.
The third thing we notice is that the trapezoidal estimate of the area under the graph, which coincides with our previous estimate based on average velocities, is exactly midway between the upper and the lower estimates. This is because the slope in line at the top of each trapezoid is the diagonal line of the 'red-green box' which represents the difference between the two estimates. It follows that as `dt shrinks, so that the difference between lower and upper estimates shrinks, the total area of the trapezoids will be 'squeezed' between these estimates. In fact, the total area under the graph of the function will also be squeezed between the lower and upper estimates. So as the difference between the lower and upper estimates shrinks to 0, all the areas (upper, lower, trapezoidal and actual areas) will necessarily approach the same limit.
Since the integral lies between lower and upper estimates, and since the difference between the lower and upper estimates approaches 0 as the interval `dt approaches 0, the integral is the limit as `dt -> 0 of either the lower or the upper sum.
We can also say that since the trapezoidal approximation of the integral is also 'squeezed' between the lower and upper sums, then as `dt approaches 0 the trapezoidal approximation is the limit of either the upper or lower sum, and the limit of the trapezoidal approximation is therefore identical to the integral.
The figure below shows the notation for the integral of the function y = sin(t^2) between t = 2 and t = 3. The elongated 'S' between the 2 and the 3 is called an integral sign, and indicates a summation in the limit as `dt -> 0; in this limit we essentially have an infinite number of terms to sum. The expression sin(t^2) dt indicates the limit of height sin(t^2) times width `dt as `dt approaches 0; dt therefore represents a limiting small `dt, so small that it doesn't actually exist. The product sin(t^2) dt represents what we sometimes call an infinitesimal quantity, so small that we have to essentially add an infinite number of them to get anything.
If the graph below represents the function y = sin(t^2) (this graph isn't really very good representation of that function; the second half-period should be much shorter than the first), then the indicated approximation of the area by upper and lower rectangles at intervals of `dt = .1 indicates a 10-increment approximation to the above integral. Refinements to greater and greater numbers of increments will yield closer in closer approximation so the integral, and in the limit as the number of increments approaches infinity so that `dt approaches zero, either the upper or lower sum will approach the integral.
The actual area under the curve is the integral, which is circled in the region beneath the curve to indicate that it represents the precise area.
"