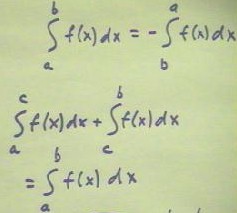
Theorems about Integrals
If we can integrate a function f(x) from x = a to x = b, the Fundamental Theorem of Calculus tells us that the result is F(b) - F(a), where F(x) is any antiderivative of f(x). We can therefore easily conclude that if we integrate f(x) from x = b to x = a, since the result F(a) - F(b) is just the negative of F(b) - F(a), we obtain the negative of the integral taken from x = paid to x = b.
This is indicated by the first equality in the figure below.
If we integrate f(x) from x = a to x = c, then from x = c to x = b, we first get F(c) - F(a), then F(b) - F(c). If we add these two expressions we obtain F(b) - F(a), which is just the integral of f(x) from x = a to x =b.
This is indicated by the second equality in the figure below.
The reason for the first equality in the figure above, which was obtained symbolically, can be understood geometrically. If a < b, then when we perform the integral from x = a to x = b our upper and lower Riemann sums will both use positive intervals `dx as we move from a to b. If our function is positive over the entire interval, then all areas will be positive. On the other hand if we go from x = b to x = a, we must use negative values of `dx and as a result give our function is positive over the entire interval all areas will be negative. Thus in the limit the integral from a to b will be positive while that from b to a will be negative.
In fact it doesn't matter whether the function itself is positive or negative at different points of the interval. If all the `dx values become negative when we reverse the direction of integration, then all the areas will reverse sign and the total area will reverse sign.
The second equality is easy to understand geometrically when c lies between a and b. The integral from a to c is simply the area under the curve between a and c, while the integral from c to b is the area under the curve from c to b. These two integrals are indicated by the shaded regions in the graph below. It is clear that when the two areas are added we obtain the area between a and b, representing the integral from a to b.
If c does not lie between a and b, the equality still holds. We can see this by noting that the area between a and b is equal to the area between a and c, minus the area between b and c. Thus the integral from a to b must be equal to the integral from a to c, minus the integral from b to c. Since the negative of the integral from b to c is the integral from c to b, we conclude that the integral from a to b is the sum of the integrals from a to c, and from c to b.
Suppose now we have the graphs of two functions f(x) and g(x), and we wish to find the integral of g(x) - f(x). Then on any interval of length `dx, the contribution to the integral of f(x) is fAve * `dx (where fAve corresponds to the average value of f(x) on the interval), and the contribution to the integral of g(x) is gAve * `dx. These contributions are indicated by the green shaded and purple shaded regions of the graph below. The contribution to the integral of g(x) - f(x) on the interval is (gAve - fAve) * `dx, which corresponds to the region between the graphs of the two functions.
Thus when we form the sum of all the (gAve - fAve) * `dx contributions, we obtain the sum of (gAve * `dx - fAve * `dx), which is the same as the sum of all gAve * `dx minus the sum of all fAve * `dx contributions. This is indicated in the figure below.
We next invoke the fact that the limit of the difference of two expressions is the difference of the limits of those expressions. This should make you uncomfortable, because while the idea makes sense, we haven't really thought deeply about the question, and we certainly haven't proved that we can treat limits like that. As an analogy, the idea that (a + b) ^ 2 = a^2 + b^2 also looks like it makes sense until you think about what it means to multiply (a + b) by itself and realize that this idea is really a very bad one (we get a^2 + 2 ab + b^2, of course). So things aren't always as simple as they look. However, having said all that, it turns out to be true that the limit of a difference of two expressions is indeed equal to the difference of the two limits.
We use this idea below to justify the statement that the integral of g(x) - f(x) over an interval is indeed equal to the difference of the integrals of g(x) and f(x) over that interval.
The dots . . . in the expression = . . . = below indicate the steps in the figure above.
The graph at the top of the figure below shows the integral of the f(x) function as the red-shaded area. The integral of the g(x) function is the purple-shaded area, which in this case includes also the entire red-shaded area. The difference between the purple-shaded area and the red-shaded area is therefore the green-shaded area between the f(x) and g(x) graphs; this region therefore represents the difference between the g(x) integral and the f(x) integral. As we have already observed, this difference is identical to the integral of the function (g(x) - f(x)).
The figure below shows a different picture of the integral of the (g(x) - f(x)) function. The top graph shows the f(x) and g(x) curves, the difference g(x) - f(x) is indicated at each of a variety of points by a vertical arrow from the f(x) value to the g(x) value.
These arrows, indicating values of g(x) - f(x), have been transported to the lower graph in order to construct a graph of g(x) - f(x). The area beneath this graph corresponds to the integral of g(x) - f(x).
The entire figure is shown below. Arrows show how the two graphs at the right of the figure represent the first integral, that of the (g(x) - f(x)) function, while the figure at the top left represents the difference between the two separate integrals. Again, the limit argument shows that the two representations give the same result.
A basic but very important theorem states that if a function f(x) is always greater than some value m over the interval from x = a to x = b, then the integral of the function between those two x values must be greater than the product of m and the length of the interval. The theorem also states the obvious analogous result for the case where f(x) is always less than some value M.
A simple way to make this plausible is to consider any interval between x = a and x = b. It is clear that for any interval, the average value of the function f(x) must be less than M and greater than m, so the contribution of that interval to the integral must be less than M `dx and greater than m `dx. When the contributions of all the intervals from x = a to x = b are added up, since all the `dx intervals at up to the total interval length b-a, the result must be between m(b-a) and M(b-a). This argument can be made more rigorous by referring to the Riemann sums that converge to the integral; the contribution of each interval to either the upper or lower Riemann sum must lie between m `dx and M `dx, and hence the sum of all contributions must again lie between m(b-a) and M(b-a).
The graph makes the result seem obvious. The line y = m must clearly lie below the graph of y = f(x) between x = a and x = b, so the rectangle beneath this line will have area m(b-a), and this area is clearly less than the area beneath the graph of f(x). A similar argument shows that the area beneath the graph is less than M(b-a).
From our original formula for the derivative of a quadratic function, you should be used to two ideas. The first idea is that the derivative of the sum of two or more functions is the sum of the derivatives; that is, the derivative of f(x) + g(x) is just f'(x) + g'(x). The second is that the derivative of constant times a function is equal to the product of the constant and the derivative of that function. In symbols, we would say that the derivative of c f(x) is equal to c f'(x).
For example, the derivative of 3 t^2 + 7 t is easily found to be 3(2t) + 7(1) = 6t + 7. Since 6t is the derivative of 3 t^2, while 7 is the derivative of 7 t, we see that the derivative of 3t^2 + 7t is the derivative of 3 t^2 plus the derivative of 7 t. We see also that the derivative of 3 t^2 is just 3 times the derivative of t^2.
It would be natural enough to apply this concept of the derivative of 12 x^5. We should obtain 12 times the derivative of x^5. Since the derivative of x ^ 5 is known by the power function rule to be 5 x^4, the derivative of x ^ 5 is 12 (5x^4) = 60 x^4. This derivative shown below.
This is in fact the correct way to take the derivative of x ^ 5, but we have not really proved this the way we approved that the derivative of a t^2 + b t + c is 2 a t + b.
We can in fact easily show that the derivative of c f(x) is c f'(x) for any constant number c (provided of course that f(x) has a derivative at x). This proof will apply to any function f(x), so we won't have to prove the result separately for power functions, then exponential functions, then trigonometric functions, etc..
We begin as shown below by writing the definition of the derivative of c f(x), shown in red below. We factor c out of the numerator in the next step, shown in purple. We then factor c all the way out of the limit, leaving as the limit just the definition of f'(x). Thus our last step shows that the desired derivative is just c f'(x).
You should be uncomfortable with something in the above proof
One step in the above prove should bother you considerably. It is the step in which we brought the constant c outside the limit. We have never proven that such thing is justified. As your experience with basic algebra errors shows you, it is always dangerous to do something you haven't justified just because it looks reasonable (who among us hasn't ever accidentally simplified (a + b) ^ 2 as a^2 + b^2, or added fractions by adding numerators and denominators, like 2/3 + 3/4 = 5/7?). It turns out that limits are in fact linear operators, so that the limit of c times an expression is equal to c times the limit of the expression and the limit of the sum of two expressions is the sum of the limits. At this point he should understand that this requires proof. We will consider such proofs later. For right now we will use at least these two properties of the limit, but we should be a bit uncomfortable every time we do until we completely justify using these properties.
Again from your experience with quadratic functions you should have the idea that the derivative of x^3 - 7 x^2 is found by taking the derivatives of the individual terms separately, obtaining 3 x^2 - 14 x. The process is shown step by step below; in the first step we separate the two derivatives, in the second we bring the constant 7 in front of the derivative of x^2, and only then do we use the rule for the derivative of a power function. The last step is an algebraic simplification.
We need to prove that the derivative of the sum of two functions is the sum of the derivatives. This proof is shown in the figure below. We first write the definition of the derivative of the function (f(x) + g(x)). We then rearrange the expression inside the limit, separating the f(x) part from the g(x) part. We then invoke the limit property mentioned above, that the limit of a sum of two expressions is the sum of the limits of those expressions, remaining a bit uncomfortable about this step. This allows us to separate the f(x) and g(x) limits, and gives us the expressions for f'(x) and g'(x).
With the properties we now have, we are completely justified (though still a bit uncomfortable about those limit steps we have justified) when we use the power function rule d / dx ( x^n) = n x^(n-1) to obtain the derivative of a polynomial. In the derivative shown below, we first separate the expression into four individual derivatives, then factor out the constant term in each derivative, and finally apply the power function rule. There is an additional step of algebraic simplification which is not shown below. You should perform this simple step to get the final expression for the derivative.
Applications of the power function formula (yes, it applies to fractional exponents; and if you have a rational function with a power function as a denominator, you can break it into two power function):
Example of a bad error: applying what works for addition and subtraction to a division. We will see in the third section how to take the derivative of a quotient of two functions, but this certainly isn't the way.
"