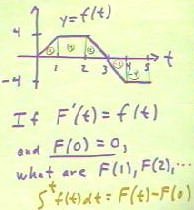
The figure below shows the graph of a function y = f(t). For the function F(t) whose derivative is f(t), and which takes the value 0 at t = 0, we wish to find F(1), F(2), etc..
At this point most of us will be pretty clueless. We obviously have to find some way of relating the function f(t) to F(t). We will then have to work out the details of how to do this for the specific function given.
The fact that the text section we're looking at concerns the Fundamental Theorem of Calculus provides a big hint. This Theorem in fact does tell us how f(t) and F(t) are related: it tells us that the integral from a to b of f(t) is just F(b) - F(a). That is, by integrating f(t) we can find differences in the values of F(t).
Since we are given F(0), we can therefore find any F(t) but simply integrating f(t) from 0 to t. The Fundamental Fair above Calculus tells us that this integral is equal to F(t) - F(0). So if we know the value of the integral at F(0), we easily get F(t). This is stated symbolically in red below (note that the lower limit 0 of the integral has been cut off in the picture).
In order to find F(1), F(2), etc., we can therefore find the integral of f(t) from 0 to 1, from 0 to 2, etc.. These integrals are easily found from the graph. It should be obvious that the area under the graph from t = 0 to t = 1 is 2 (the height of the graph goes linearly from a 0 to 4, for an average height of 2, over a run of 1, giving area 2 * 1 = 2). The integral from t = 0 to t = 2 adds the area 4 under the graph from t = 1 to t = 2, giving and integral value of 6. The next interval adds area 2, so that the integral from t = 0 to t = 3 is 8. The remaining two areas are both negative, and when added to the existing area give us integrals of 6 and 2, as shown below.
The equalities shown below, together with the fact that F(0) = 0, allow us to easily find F(1), F(2), etc..
A text problem states that the monthly dollar rate of income change is r(t) = 40(1.002) ^ t, and asks for the change between two given months. For example, if we wish to find a change in income between t = 6 and t = 18 months, our reasoning will proceed as follows:
The interpretation of the graph of r(t) vs. t will show us what we need to do to answer this question. If we consider a trapezoid of width `dt, we see that its altitudes represent the rates, in dollars per month, at which income changes while `dt represents the number of months over which the average rate applies. The slope of this trapezoid will be the rate at which the rate changes, which does not seem relevant to this problem. The area under the trapezoid will represent the product of the average rate at which income changes and the time interval, which will give us the change in income.
The area under a trapezoid of course gives us only an approximation of the actual area under the graph. To get the precise area, we integrate the rate function between limits specified by the situation. In this case we integrate the rate function between t = 6 and t = 18. The integrals are indicated in purple. The DERIVE syntax for the integral would be INT( 40 * 1.002^t, t, 6, 18), and we could use DERIVE to evaluate the integral. We will soon see the expressions for derivatives of exponential functions, which we could then use to find an antiderivative and evaluate the integral ourselves.
As an exercise we compute the derivative of y = 3 t^2 - 12 / `sqrt(t) - 1/t^2, as shown below. This function is not a polynomial, but our technique for taking its derivative is the same as if it was a polynomial. We first express each term as a power function, obtaining the expression 3 t^2 - 12 t^(-1/2) - t^(-2). We then apply the power function rule to each term and simplify. In the last step we express our result in the form of the original function, with no negative exponents.
A text problem asks for what values the derivative of the function f(x) = 4 x^3 + 6 x^2 - 32 x + 7 is greater than 1. And obvious way to begin to answer this question is to take the derivative. We obtain 12 x^2 + 12 x - 23. The condition that this derivative be > 1 gives us the first inequality, in green, below. We note that the left-hand side of this inequality is a quadratic, which leads us to subtract one from both sides of the inequality to obtain a more standard form of the quadratic, with zero on the other side of the inequality.
To determine where 12 x^2 + 12 x - 24 > 0, we sketch or graph of 12 x^2 + 12 x - 24. We notice that this graph is a parabola opening upward, which might well give us positive values to the right and left of zeros and negative values between the zeros. Thus in order to find the regions where the expression is > 0, we can begin by finding the zeros of the function.
The expression will be zero forever 12 x^2 + 12 x - 24 = 0. We could just use the quadratic formula and find the zeros, but it is really easy to first multiply both sides by 1/12 to obtain x^2 + x - 2 = 0. We notice that this expression easily factors, so in this case we can completely avoid the quadratic formula. We obtain x = -2 and x = 1.
Noting that the function whose zeros we have found represents f'(x) - 1, we see that f'(x) - 1 is positive whenever x < -2 or x > 1, and negative when -2 < x < 1. This is significant because f'(x) - 1 > 0 is identical to f'(x) > 1. Thus f'(x) > 1 for x < -2 and for x > 1.
Consider now the function y(t) = 350 - 4.9 t^2, which represents the altitude of object dropped at t = 0 from a height of 350 meters. We wish to find the velocity function, the acceleration function, the time when the object strikes the ground and its velocity at that time.
We first note that the velocity is the rate of change of the position of the object, so that the position function y(t) yields they velocity function v(t) = y'(t). We easily take the derivative all of the position function to obtain v(t) = -9.8 t.
The acceleration of an object is the rate which its velocity changes, so the acceleration function will be the derivative of the velocity function or the second derivative of the position function. We easily take the derivative of the velocity function to obtain acceleration function a(t) = -9.8.
The object strikes the ground when y(t) = 0. This provides us with an equation 0 = 350 - 9.8 t^2 for the value of t at the instant the object strikes the ground. We easily solve this equation to obtain t = 8.4: the object strikes the ground 8.4 seconds after it is released.
If we wish to find the velocity when the object strikes to ground we simply substitute t = 8.4 into the velocity function v(t) = -9.8 t. We obtain v(8.4) = -82, representing a downward velocity of 82 meters/second.
As you should know, the volume of a sphere of radius r is V = (4/3) `pi r^3. Regarding V as a function of r, we can easily calculate the derivative dV / dr = 4 `pi r^2. We note that this expression is equal to the surface area of the sphere.
To interpret this derivative we note that dV / dr is the limiting value of `dV / `dr, the ratio of volume change to change in radius. That is, dV / dr gives us the volume change per unit of change in radius. If we multiply dV / dr for a given radius by a change in radius, we will get the approximate volume change (more accurate for smaller radius changes).
We can visualize these quantities in terms of a sphere of radius r and the sphere we get when the radius increases by `dr. The difference in volume is the volume of the spherical shell between the first and second sphere.
The derivative of an exponential function
We begin by looking at the definition of the number e. There are two possible definitions. The first is e = lim [h -> infinity ] (1 + 1/h) ^ h). The second definition, completely equivalent of the first, is e = lim [h -> 0] ( 1 + h ) ^ (1/h). To understand these two definitions, and to see why the definitions are equivalent it helps to evaluate the first expression for h = 1, 2, 10 and 1000, and the second expression for h = 1, 1/2, 1/10 and 1/1000. In either case we get numbers approaching approximately 2.718 (more precisely 2.718281828 ..., where the ... is not a repetition of 1828, where in fact there is never a systematic repetition that is not eventually broken). The actual limit, which is an irrational number, is called e.
Now it follows that e^x = ( lim [h -> 0] (1 + h) ^ (1/h) ) ^ x. By another as yet unproven but valid property of limits, we can take the exponentiation inside the limit, obtaining the expression in the third line below (we just multiply exponents; remember to be a little uncomfortable since you don't know exactly why we can take the exponentiation inside the limit).
If we now let k = x/h, so that h = x / k, we obtain lim [k -> infinity] (1 + x/k) ^ k). The binomial expansion of (1 + x/k) ^ k is 1 + k * (x/k) + k (k-1) / 2 * (x/k)^2 + ... . If x is small, higher and higher powers of x become less and less significant, and we are left with the approximate expression e^x = 1 + k * (x/k) = 1 + x. Thus for small values of x, e^x = 1+x is a good approximation. (You can check this on your calculator. If the approximation holds e^.01 should be close to 1 + .01 = 1.01, and e^.001 should be even closer to 1 + .001 = 1.001).
We can now write and simplify the expression for the derivative of e^x. This expression is written out in the figure below. We see that by the laws of exponents (specifically x^(a+b) = x^a * x^b) the numerator e^(x+h) - e^x is equal to e^x e^h - e^x. This is represented in the second line.
We note that we can factor e^x out of the numerator of our limit. Not only that, since h does not appear in e^x, e^x can be regarded as a constant and taken completely outside the limit. The resulting expression gives us the third line in the figure below.
Now for small h, the numerator e^h - 1 can be rewritten as (1 + h) - 1. Since where taking the limit as h approaches 0,we can certainly use this fact to write the fourth line.
Now we just do a little algebra to get the last line. (1+h) - 1 is immediately simplified to h, and h/h is obviously 1, so the limit is just 1. Thus we conclude that d / dx (e^x) = e^x.
The graph in the figure below gives a graphical interpretation of this result. On a graph of y = e^x, the height of the graph that any value of x is y = e^x. The slope of the tangent line at this graph point is equal to the derivative y' = e^x. Thus the slope of the graph is equal to its height above the x axis. As x increases the slope of the graph increases, faster and faster for larger values of x.
We now ask how we might find the derivative of a function like y = 3 ^ x (see the above figure). We note that by the laws of exponents and logarithms (specifically e ^ ln(a) = a and e^(a*b) = (e^a) ^ b), 3^x can be written as e^(x ln(3)). (You should use the laws to simplify e ^ (x ln(3)) in order to be sure you see this).
It follows from the chain rule for composite functions, which we have not yet covered but will soon and which should therefore make you somewhat uncomfortable, that the derivative of y = 3^x = e^(x ln(3)) is just y' = ln(3) * 3^x.
We can use the same reasoning to show that y = a^x can be expressed as y = e^(x ln(a) ), which has derivative y' = ln(a) e^(x ln(a)), which simplifies to y' = ln(a) * a^x.
You should think about the details of this reasoning process, but in the end the most important thing you should recall for the purposes of the present assignment is that
(d / dx) (e^x) = e^x and (d / dx) (a^x) = ln(a) * a^x.
The derivative of the e^x function is just e^x itself; the derivative of the a^x function is just a^x itself, but multiply by a 'correction factor' ln(a).
"