Overview, the Flow Model, Summaries of the Modeling Process
The flow model, up to solution of the simultaneous equations
Exercises based on the introductory model
A brief summary of the steps of the modeling process
A briefer summary of the modeling process, with pictures
A really brief summary of the modeling process, in outline form
An assignment of information to be memorized for this course.
Depth vs. time for water flowing from a uniform cylinder through a uniform hole near the bottom
When water is allowed to flow freely from a uniform hole in the side of a uniform cylinder, with no water added to the cylinder after the flow begins, the depth of water in the cylinder will obviously decrease. What is not completely obvious is whether the depth increases at a constant rate, at a decreasing rate or at an increasing rate.
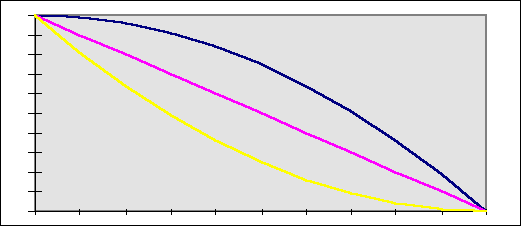
The majority of the class predicted that water would flow out at a decreasing rate, so that depth would change more and more slowly. A significant number of participants predicted that the water would flow out at a constant rate, while a few predicted an increasing rate. These behaviors are depicted on the graph below. Each graph depicts depth vs. time, with depth on the vertical axis and time on the horizontal axis. One function predicts that the water would flow at a constant rate, while on another in would flow at an increasing rate and on a third it would flow at a decreasing rate.
The actual flow was observed using a simple computerized timer. Depths of 90, 80, 70, ..., 10, 9, 8, ..., 2 centimeters (above the hole) were marked on a clear uniform cylinder and the clock times and time intervals were recorded. It was observed that the flow for each 10-cm interval required a longer time than for the preceding interval, which was seen to clearly indicate a decreasing rate of flow.
Participants were then asked to pick three representative data points from their depth vs. time tables, and to plot these points. Typical graphs looked like the following:
It is clear that this graph depicts a depth that is decreasing at a decreasing rate.
Of course the remaining points could have been plotted, and will be plotted as homework.
A Mathematical Model
It would be useful to have a mathematical rule, or function, that allows us to compute the depth for any given time, or the time for any given depth. Such a rule would be called a mathematical model of the flow depth vs. time.
For example, suppose that the three data points were (30, 49), (60,16) and (90,1), where the coordinates of a point represent time and depth, in that order. A mathematical model for these three data points would be
depth = .01 t^2 - 2t + 100.
When t = 30 is substituted into this model, we obtain depth = .01(30^2) - 2(30) + 100 = 49, which coincides with the data point (30,49). You should check for yourself that when t = 60 and t = 90 are substituted into the above model, we obtain depths of 16 and 1, respectively. Note that this is consistent with the data points (60,16) and (90,1).
You should note also that the depth function is of the form depth = a t^2 + b t + c, which is a quadratic function. Any time we have three data points with different t values, we can find a quadratic function that fits these three points exactly, in the above sense: all three data points can be exactly validated as above. We will see soon how this is done.
The above model was based on three data points. Suppose that other data points included (20,63) and (50,27). We do not expect that these points will necessarily fit the model exactly, since the model was obtained from the original three points. We can check to see how close (20,63) is to the model by substituting t = 20 to see how close our result is to 63. Check for yourself that when t = 20, we obtain depth = 64, which differs from the observed depth of 63. The observed depth differs from a model by -1, since 63 is one unit less than 64. You should check that the other data point (50,27) differs from the model by +2.
The quadratic formula
The quadratic formula is contained in the following statement, which you are required to know verbatim:
If y = a x^2 + bx + c, then y = 0 if, and only if, x = [ -b +- `sqrt(b^2 - 4ac) ] / (2a).
Note that tests for Precalculus I (Mth 163) not infrequently ask for the full statement of the quadratic formula. The above is the only statement that will be accepted for full credit, should this question appear on a test.
This formula is more familiar when written out in more standard mathematical notation. However, it is not presently feasible to use standard mathematical notation on Internet documents, and in addition to the disadvantages (like being harder to read) there are advantages to the linear notation used above. For example it is essential to understand why the denominator 2a must be in parentheses, as must the numerator. This notation forces the user to direct careful attention to the order of operations.
This statement of the quadratic formula can be used to analyze a quadratic mathematical model of the flow depth function. Specifically we will be able to use the statement to determine the time when the depth reaches any given level, or to determine those depths which will never be reached.
Simultaneous linear equations
You should recall having seen systems of simultaneous linear equations something like the following:
2x + 7y = 9
3x - 4y = 5.
Hopefully you recall that if we multiply the first equation by 3 and the second by -2, we obtain
6x + 21y = 27
-6x + 8y = -10.
Adding these two equations we obtain
0x + 29y = 17,
which can be written simply as
29y = 17.
Of course we can easily find y if we divide both sides by 29. However you know that very well, and that is not the point here. The point is that we have combined the two equations to eliminate one of the variables, which is what permits us to solve for the other variable.
We will look more closely at how to solve systems of equations shortly. However, right now we are more interested in obtaining a system of equations to be solved in order to model the depth vs. time behavior of the water in the cylinder.
Obtain simultaneous linear equations in order to find a quadratic model of three data points
Suppose you hadn't been told above what the model was for the depth function that fits the points (30,49), (60,16) and (90,1), but that you did somehow know that a quadratic function
depth function: depth = a t^2 + bt + c
would fit the points, if only you could find the values of a, b and c. You could obtain an equation for each data point, as follows:
For the first data point (30,49), we see that when t = 30, depth = 49. If we substitute these values into the general quadratic function depth = a t^2 + bt + c, we obtain
49 = a (30^2) + b(30) + c,
or, with a little rearrangement,
900 a + 30 b + c = 49.
Using the second data point (60,16) in the same way we obtain
3600 a + 60 b + c = 16.
Similarly the third data point (90,1) gives us the equation
8100 a + 90 b + c = 1.
These three equations give us the 3-equation system
900 a + 30 b + c = 49
3600 a + 60 b + c = 16
8100 a + 90 b + c = 1.
Once the equations have been found we can solve them to obtain the values of a, b and c, which are then substituted back into the form depth = a t^2 + b t + c. You might or might not know how to solve this system; the solution process will be discussed later. In any case, it turns out that for this system we obtain a = .01, b = -2 and c = 100, giving us the previously stated function
depth function for three chosen points: depth = .01 t^2 - 2t + 100.
We aren't worried about actually solving this system just yet (in case you are curious, we use elimiination much as in the earlier example; although this one has messier numbers and requires a bit more work, it's not that much harder). The process of substituting data points into the form of a function is simple enough. You should check your understanding by obtaining the linear equations for a, b and c that correspond to the data points (20,63), (50,27) and (70,10).
Here are some data for the temperature of a hot potato vs. time:
Time (minutes)
Temperature (Celsius)
0
95
10
75
20
60
30
49
40
41
50
35
60
30
70
26
Graph these data below, using an appropriate scale:
Pick three representative points and circle them.
Write the equations that result from the assumption that the appropriate mathematical model is a quadratic function y = a t^2 + b t + c.
Eliminate c from your equations to obtain two equations in a and b.
Solve for a and b.
Write the resulting model for temperature vs. time.
Make a table for this function:
Time (minutes)
Model Function's Prediction of Temperature
0
10
20
30
40
50
60
70
Sketch a smooth curve representing this function on your graph.
Expand your table to include the original temperatures and the deviations of the model function for each time:
Time (minutes)
Temperature (Celsius)
Prediction of Model Deviation of Observed Temperature from Model 0
95
10
75
20
60
30
49
40
41
50
35
60
30
70
26
Find the average of the deviations.
Comment on how well the function model fits the data. (Note: the model might or might not do a good job of fitting the data. Some types of data can be fit very well by quadratic functions, while some cannot).
Carefully read and understand the outlines and summaries of the modeling process as given below, as it applies to the examples discussed so far. Be sure to note the outline to be memorized (see the end of the page or click on the link To Be Memorized).
Summary of Modeling Process, Version 1
The Modeling Process for the Flow Depth vs. Time Phenomenon
The modeling process can be broken into a number of steps. The general process as described here for the flow situation can be applied to a wide range of real-world situations. The details encountered in different situations, such as the nature of the observations, the type of mathematical function used, the number of data points selected, etc., might vary from one situation to another. However, the overall steps will be pretty much the same as those outlined here.
The steps are as follows. You should recognize these steps from your work on the flow experiment:
Orient
For the flow situation, we visualize the flow and we sketch a graph representing depth vs. clock time, as we expect it to occur. This step helps to focus our attention on what we are about to observe. It helps 'get the wheels turning' in our minds.
Observe
For the flow situation, we observe depth vs. time. We do this by marking the cylinder at various depths and using a timer to determine when each depth is attained.
Organize Data
Organize the observed data into table(s). Note the patterns in the numbers on the table(s) and try to visualize the corresponding graph(s).
Graph
Graph the observed data, with the dependent variable on the y axis, the independent variable on the x axis.
Postulate
Postulate a model (we postulate a quadratic model for flow depth vs. time; for other situations we might postulate an exponential model, a power-function model, a logarithmic model, a linear model, or any of a variety of other possible models).
Note: At this point you probably don't have a good understanding of these different types of functions; that understanding is the primary goal of your course. As the course progresses we will learn a great deal about linear, quadratic, exponential, logarithmic and polynomial functions. In a precalculus course we learn the basic algebraic properties of these functions. In a calculus course we develop more powerful tools such as differentiation and integration to analyze these functions and apply them to more advanced situations.
Select Representative Points
Pick an appropriate number of representative data points (three for the quadratic model used with the flow depth phenomenon, one for each parameter a, b and c in the model depth = a t^2 + b t + c). Note that these points are to represent the data set as well as possible, and need not be actual data points.
Obtain an equation for each selected point
Substitute the coordinates of the data point into the model. In the flow depth vs. time situation we obtain for each point an equation with a, b and c as unknowns (e.g., 900 t^2 + 30 t + 1 = 4900).
Solve the system of equations
Use whatever techniques are required to solve the system of equations. Usually these techniques will involve eliminating variables. Computerized algebra programs will also be used. For the flow depth vs. time situation we might obtain parameter values like a = .01, b = -2, c = 100.
Substitute parameters
Substitute the values of the parameters into the general form of the model to get the specific model. For the flow depth vs. time situation, we substitute the values for a, b, and c into the general form depth = a t^2 + b t + c to obtain a specific model ( e.g., if a = .01, b = -2 and c = 100, we get depth = .01 t^2 - 2 t + 100).
Graph the model
Graph the model along with the data points and compare the model with the data. The model will usually be a straight or curved line, obtained by graphing the function. The model will compare well with the data when all the data points lie close to the graph of the function, and when there is no apparent pattern to how the data points deviate from the function.
Quantify the comparison
Determine how much each data point deviates from the prediction of the model. This deviation appears on the graph as the vertical distance from the data point to the graph of the function. We then average the magnitudes of these deviations. In the flow depth vs. time situation we evaluate the model function for the time of each data point, and compare the resulting depth prediction to the observed depth by taking the difference between prediction and observation. We finally average the deviations to obtain a number for the 'average closeness' of the model and the observations.
Pose and answer questions
Use the model to determine such things as the value of the dependent variable given the value of the independent variable, or vice versa. For the flow depth vs. time situation, the model permits us to determine the depth for a given time (just substitute the time for t and we get the depth), or the time at which a given depth occurs (just substitute the desired value of the depth to get an equation which can be solved using the quadratic formula).
Do the science: relate the mathematics to the real world.
The step is actually optional in this course, since we are concerned with the mathematics and not the science. It is included here for completeness, and because often the science is pretty simple and enhances our understanding of the mathematics. What science does is tries to figure out why the model is or is not appropriate to the situation. Science might use the model to speculate on the underlying mechanism or process. The science of the flow depth vs. time situation relates pressure to the velocity of the escaping fluid in order to explain the model.
Summary of Modeling Process, Version 2
Here we represent the same process as in Version 1, but this time in brief phrases, equations and pictures.
Orient
Predictions, speculations.
Observe
Set up and take data.
Organize Data
time depth 30
49
60
16
90
1
Graph
Postulate
quadratic function depth = a t^2 + bt + c ????
Select Representative Points
Obtain an equation for each selected point
400 a^2 + 20 b + c = 61
1600a^2 + 60 b+ c = 13
8100a^2 + 90 b+ c = 2
Solve the system of equations
a = .01, b = -2, c = 100
Substitute parameters
depth = .01t^2 - 2 t + 100
Graph the model
Quantify the comparison
time
observed values
prediction of model
deviation
0
95
97
-2
10
75
74
+1
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
Average of deviations = 2.43
Pose and answer questions
Do the science: relate the mathematics to the real world.
Pressure is proportional to depth.
Energy conservation implies that velocity is proportional to square root of pressure.
Thus dy/dt = k `sqrt(y).
Therefore velocity is quadratic in time.
Summary of Modeling Process, Version 3This is a condensed version of the process in outline form. This outline will be used throughout the course and should be memorized.
A. Obtain and Represent Data
A2. Observe
A3. Organize Data
A4. Graph
B. Obtain a Model
B1. Postulate
B2. Select Representative Points
B3. Obtain an equation for each selected point
B4. Solve the system of equations
B5. Substitute parameters
C. Validate and Use the Model
C1. Graph the model
C2. Quantify the comparison
C3. Pose and answer questions
C4. Do the science: relate the mathematics to the real world.
To Be Memorized
The above outline of the model is to be memorized. At any time during the course, on any test or quiz, you might be asked to write down this model and illustrate the meaning of one or more of the steps.
This outline will be more or less followed throughout the course.