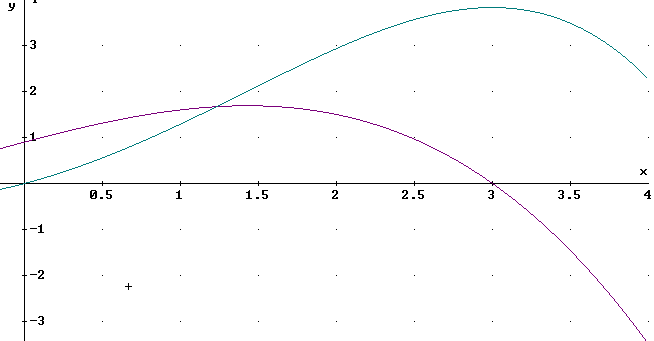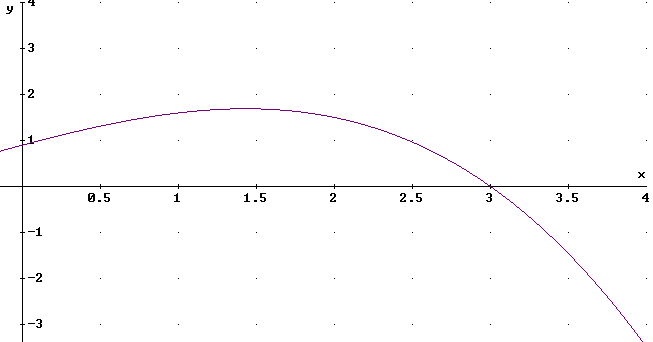
Calculus II Class 01/08

Find antiderivatives of:

1.  t^2

An antiderivative is 1/3 t^3, since (1/3 t^3) ' = 1/3 ( t^3) ' = 1/3 ( 3 t^2) = t^2.  The general antiderivative is t^2 + c.

2.  4/3 t^-5

An antiderivative of t^-5 is a multiply of t^-4; since the derivative of t^-4 is -4 t^-5 an antiderivative of t^-5 would be -1/4 t^-4.

An antiderivative of 4/3 t^-5 would therefore be 4/3 ( -1/4 t^-4) = -1/3 t^-4, and the general antiderivate would be -1/3 t^-4 + c.

3.  2 / ( 3 t^2)

We first rewrite as 2/3 t^-2.  An antiderivative of t^-2 is -t^-1, so the general antiderivative of 2 / (3 t^2) + c = 2/3 ( - t^-1) + c = -2/3 t^-1 + c , or -2 / (3 t) + c .

4.  e^(5x)

Recall that the derivative of e^x is e^x, so e^x is its own antiderivative.

The derivative of e^(5x) is 5 e^(5x), by the chain rule.  So if we take the derivative of 1/5 e^(5x) we'll get e^(5x).  Thus the general antiderivative of e^(5x) is 1/5 e^(5x) + c.

5.  sin(t)

Recall that (sin(t)) ' = cos(t) and (cos(t)) ' = - sin(t).

The general antiderivative of sin(t) is seen to be - cos(t) + c.

6.  cos(3x)

We want to say that the antiderivative is something like sin(3x), but (sin(3x)) ' = 3 cos(3x) so we gotta use 1/3 sin(3x) + c as the general antiderivative.

7.  sqrt(z)

sqrt(z) = z^(1/2).  Antiderivative is a multiple of z^(1/2 + 1) = z^(3/2).  Derivative of z^(3/2) = 3/2 z^(1/2) so antiderivative of sqrt(z) must be 2/3 z^(3/2) + c.

8.  1 / t. 

Good idea that won't work:

1/t = t^-1.  Antiderivative should be 1 degree 'higher', which should be a multiple of t(-1 + 1) = t^0.  But t^0 = 1, and the derivative of 1 ain't 1/t.  No way.

Reality check:  Derivative of ln(t) is 1/t.  So antiderivative of 1/t is ln(t).

9.  1/t^2

Bad idea that seems good until you check it out:  ln(t^2).  (ln(t^2)) ' = (t^2) ' * 1/ t^2 = 2 t / t^2 = 2 / t, not 1 / t^2.

Good idea:  1 / t^2 = t^-2, which has antiderivative -t^-1 + c.

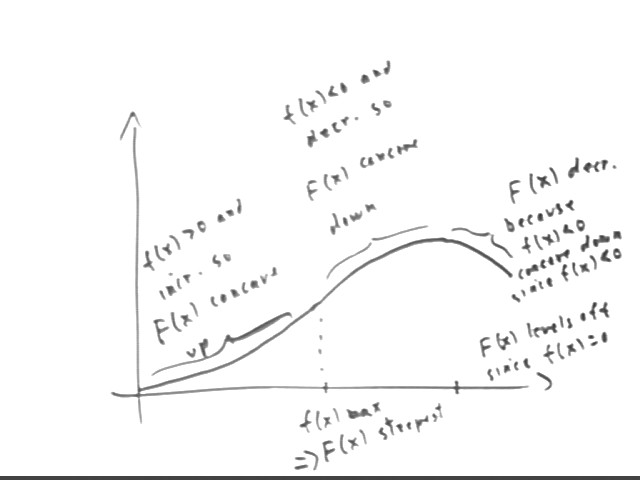
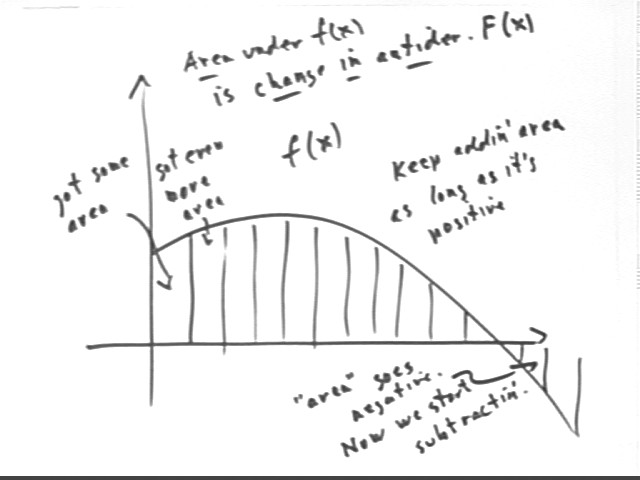
Plot the antiderivative F(x) of the function f(x) shown on the graph below from x = 0 to x = 4, assuming that F(0) = 0.

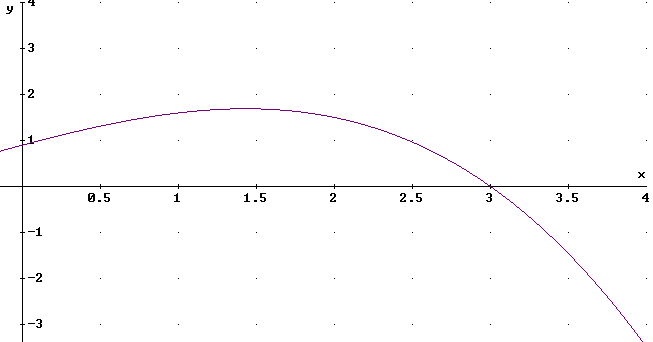
The change in the antiderivative function F(x) between two values of x is characterized in the following ways:

• The change in F(x) is equal to the area under the f(x) graph between those two values (provided we consider area as being positive or negative depending on whether f(x) is above or below the x axis).
• The change in F(x) is can be thought of as the change in the amount function for which f(x) is the rate function; you should be familiar with the reasons for which this is equal to the area under the graph, and should review this idea.

For the given function we can think of dividing the given x interval into segments. 

• The first segment has positive area, so F(x) will change by a positive amount over this interval.  Since F(x) = 0 when x = 0, this will give F(x) a positive value at the end of the first interval.
• The second segment has even more area than the first, resulting in a greater change F(x) over the second subinterval.  Assuming that interval lengths are constant, this means that the average slope of the F(x) graph will be greater over the second interval than over the first.
• Positive area keeps accumulating as long as f(x) > 0, which happens up to x = 3.  So F(x) will be increasing for 0 < x < 3.  The rate of increase, and hence the slope of the F(x) graph, will increase as long as f(x) increases, then the rate of increase will decrease.  So the F(x) graph will be increasing at an increasing rate, hence concave up, as long as f(x) is positive and increasing; and F(x) will be increasing at a decreasing rate, hence increasing and concave down, as long as f(x) is positive and decreasing.
• As f(x) goes from positive to negative the graph of F(x) will stop increasing and begin decreasing, becoming 'level' for an instant when f(x) = 0.

These behaviors are shown in the two graphs below.

We also note that, as should be clear from the above explanation, the slope of the F(x) graph will be equal to the y value of the f(x) graph.  So the slope of the F(x) graph starts out at about +.9, increases to a maximum of about +1.7 in the vicinity of x = 1.4, decreases to zero at x = 0 and becomes negative past x = 3.

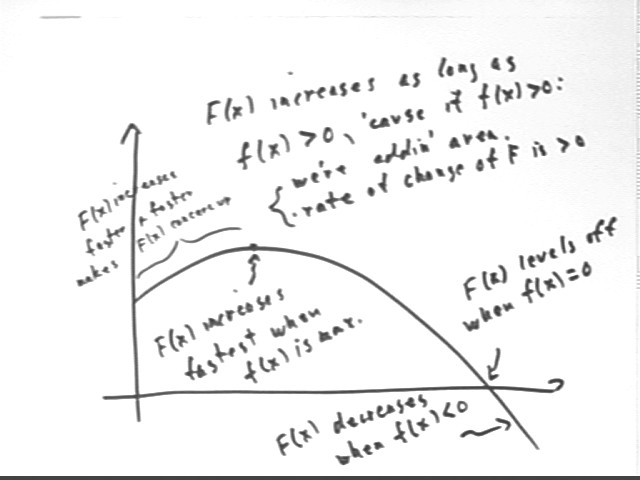
An approximate graph of F(x) vs. x is shown in the figure directly below. 

An accurate graph of F(x) and f(x) is depicted in the second figure below.