Calculus II Class 01/10

Notes to be completed by 1/11/03

Find antiderivatives F of the functions f given below:

1.  sin(x-1)

This is of the form sin(u) with u = x - 1.

Since (x-1)' = 1 the Chain Rule will leave us alone and we see that the general antiderivative is F(x) = -cos(x-1) + c.  

To check we take the derivative and easily find the F ' (x) = sin(x-1).

2.  e^(2x + 4)

This is of the form e^u with u = 2 x + 4.

Since (2x + 4) ' = 2, the Chain Rule ain't gonna leave us alone and we have to write F ( x ) = a e^(2 x + 4) + c, for some value of a and arbitrary value of c.

We know that F ' (x) = e^(2 x + 4) so we have 

• a * (2 x + 4) ' * e^(2 x + 4) = e^(2 x + 4)
• 2 a e^(2 x + 4) = e^(2 x + 4) therefore
• a = 1/2 

Our general antiderivative function is therefore F(x) = 1/2 e^(2 x + 4) + c.

3.  1/ ( t - 3)

This is of the form 1 / u with u = t - 3.  

Since (t-3) ' = 1 the Chain Rule gonna leave us alone agin.

Our general antiderivative is therefore F(t) =  ln | t - 3 | + c.  Note that the domain of this function includes all real numbers except 3.

4.  (t - 7) ^ 20

This is of the form u^20 with u = t - 7.  (t - 7) ' = 1 so the Chain Rule doesn't affect our conclusion that the general antiderivative is 

F(x) = 1/21 * (t - 7) ^ 21.

Now let's think about finding an antiderivative of e^(x^2).  This is of the form e^u with u = x^2.  Since u ' = (x^2) ' = 2x we're tempted to say that F(x) = 1 / (2x) * e^(x^2) + c. 

However F ' (x) = 

[ 1 / (2x) ] ' * e^(x^2) + 1 / (2x) * [ e^(x^2) ] ' = 

- 1 / (2 x^2) * e^(x^2) + 1 / (2x) * 2x e^(x^2) = 

-1 / (2 x^2) e^(x^2) + e^(x^2).

This attempt at constructing F ' ( x ) does NOT give us a result which is equal to f(x).  

The flaw in our attempt was that when we multiplied by 1 / (2x) we weren't multiplying by a constant, as we were in Problem 2.  Thus when we took the derivative of our attempted F(x) function we had to use the product rule, which gave us the confounding term -1 / (2x^2) e^(x^2).  This term ruined our attempt to contruct a valid antiderivative (note that the other term of F ' (x) was e^(x^2), exactly what we wanted).

It turns out that there is no way to express any antiderivative of e^(x^2) as a combination of simple functions.  This would also be the case for sin(x^2), cos(x^2), and almost any other composite function where the 'inner' function is not linear.

In rare cases, for example x e^(x^2) or x sin(x^2), we can construct an antiderivative.  Chapter 7 will consist of techniques for antiderivatives for certain types of functions.

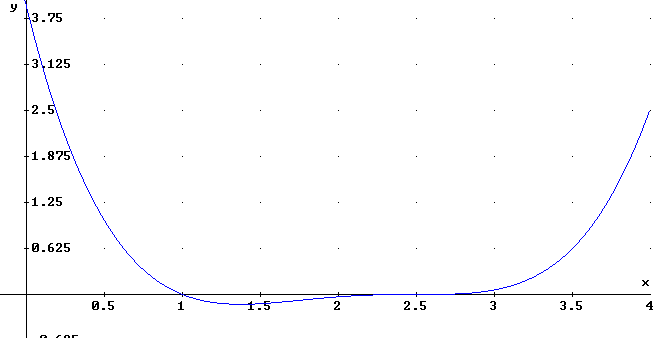
Plot the antiderivative F(x) of the function f(x) shown on the graph below from x = 0 to x = 4, assuming that F(0) = 0.

(z-2.5)^3/4*(z-1), 0 to 4 both axes

There are two ways to construct the graph of the F(x) function. 

The first way is to use the principle that the slope of the graph of the antiderivative function F(x) is equal at each point to the value of the f(x) function.

At x = 0 we have f(x) = 3.9, approx.  This means that the slope of the F(x) function, which by the given conditions starts at (0, 0), must be 3.9.  Check the graph below to see that this is the case (sketch a tan line and see that its slope is close to 3.9).  When sketching the graph yourself you should start by sketching a short segment thru (0, 0) having slope 3.9.

By the time x = 1 we see that f(x) has decreased to 0.  So the slope of F(x) at the x = 1 point will be zero. 

Positive f(x) implies that F(x) has positive slope, is hence increasing; while negative f(x) will be associated with decreasing F(x).

Decreasing f(x) implies that the slope of the F(x) graph is decreasing, making the F(x) graph concave down.  Increasing f(x) is associated with F(x) being concave up.

So for the present situation:

• Since f(x) is positive F(x) will be increasing for 0 < x < 1.
• Since f(x) is decreasing over this interval F(x) will be concave down.

• F(x) will be decreasing for 1 < x < 2.5

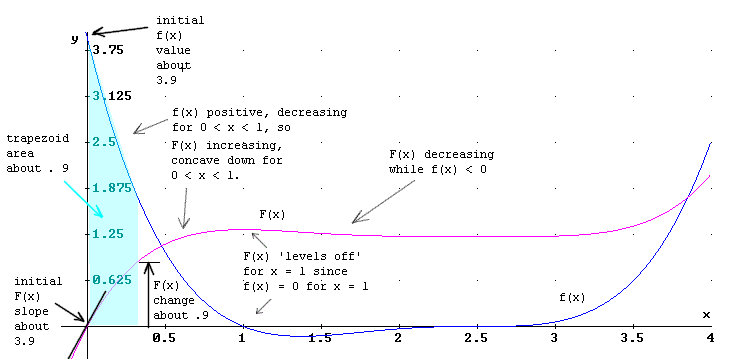
The second approach to graphing is to partition the x interval into a number of subintervals, and use a trapezoidal approximation.

A trapezoidal approximation of the area under the f(x) curve between x = 0 and x = .3 is approximately area = .9.  This area will be equal to the approximate change in the F(x) function between x = 0 and x = .3.  You should verify from the  above graph, where the area under the f(x) curve for 0 < x < .3 and the change in F(x) over the same interval are indicated,  that this is the case.

A trapezoidal approximation of the area under the f(x) curve between x = .3 and x = .6 is approximately area = .4.  This area will be equal to the approximate change in the F(x) function between x = .3 and x = .6.  You should verify from the  above graph that this is the case.  This interval is not shown on the above graph; you should label a copy of this graph to show this.

The connection between the slope model and the area-as-change-in-F(x) model is near the heart of both the theory and applications of Calculus.

In terms of the above example we see that if F(x) changes by .9 over the   interval 0 < x < .3  with `dx = .3, then the average slope over that interval is rise / run = .9 / .3 = 3.  If f(x) gives the slope of F(x) then this average slope should match the average value of the f(x) graph over the same interval.   You should verify that this is the case.

Conversely if the average slope of the F(x) graph over the interval 0 < x < .3 is equal to the average value, approximately 3, of the graph of f(x) then the change in F(x) must be 3 * .3 = .9.

Going back to the flow model we think of f(x) as the rate of depth change and F(x) as the depth.  We see that the change in depth is equal to the product of the time interval and the average rate of change, while the average rate of change of the depth is equal to the change in F(x) divided by the time interval.