
Calculus II Class 01/15
Calculus I Quiz 0115
Find the general solution of dy/dt = 1.2 t, then give the specific solution for which y(0) = 10.
If dy/dt = 1.2 t then y is an antiderivative of 1.2 t, with respect to t. The general antiderivative is
y = 1.2 ( t^2 / 2) * c = .6 t^2 + c.
If y(0) = 10 we have
10 = 6. * 0^2 + c so that
c = 10
and our solution becomes
y = .6 t^2 + 10.
Find the general solution of dy/dt = 12 cos(t), then give the specific solution for which y(0) = 7.
Again we see that y is a general antiderivative with respect to t of 12 cos(t) so that
y = 12 sin(t) + c.
Since y(0) = 7 we have
7 = 12 sin(0) + c so that
c = 7
and our particular solution is
y = 12 sin(t) + 7.
Find the general solution of dy/dt = 1.2 / t, then give the specific solution for which y(1) = 2.
Our general solution is
y = 1.2 * ln(t) + c.
Since y(0) = 2 we have
2 = 1.2 * ln(1) + c or since ln(1) = 0
c = 2
giving us particular solution
y = 1.2 * ln(t) + 2.
Find the definite integral of x^2 with respect to x, between x = 1 and x = t. What is the derivative with respect to t of this result?
The definite integral of f(x) = x^2 with respect to x is the change in an antiderivative function between the two limits x = 1 and x = t.
Using antiderivative function F(x) = x^3 / 3 we find that the definite integral is
definite integral = F(t) - F(1) = t^3 / 3 - 1^3 / 1 = t^3 / 3 - 1/3.
The derivative of this definite integral with respect to t is
(t^3 / 3 - 1/3) ' = t^2.
Note that this is just f(t).
This is an instance of the Second Fundamental Theorem of Calculus, shown below in standard notation and expressed in 'typewriter notation' as
d/dt [ int(f(x), x, 1, t) ] = f(t).
In terms of a depth-and-rate interpretation, f(x) is the rate-of-depth-change function and the integral of this function between x = 1 and x = t is equal to the change in the depth function between x = 1 and x = t.
x can be thought of as a 'dummy variable' in fact representing clock time; we need to use the dummy variable because clock time is one of the limits (i.e., 1 and t) on the interval of integration.
The integral runs from a specific instant 1 to a variable instant t. So the integral gives us a variable function F(t) of t.
The variable function F(t) which represents the integral is in this case a change-in-depth function, so its derivative must be the original depth function f(t), expressed now in terms of clock time t instead of the dummy variable x.

Find the definite integral of e^(2x) with respect to x, between x = 1 and x = t^2. What is the derivative of this result?
Antiderivative is F(x) = 1/2 * e^(2x), so the definite integral is
definite integral = F(t^2) - F(1) = 1/2 * e^(2 t^2) - 1/2 e^(2 * 1).
The derivative of this result is d/dt [ 1/2 * e^(2 t^2) - 1/2 e^(2) ] = 2 t e^(2 t^2).
Had we followed the form of the last problem we might have first expected that the derivative would be just f(t), though on a little thinking we would see that t^2 is the upper limit, not t, so we might have expected f(t^2).
However f(t^2) is just e^(2 t^2), not our result, which was 2t e^(2 t^2).
The problem is that t^2 is itself a function with a derivative other than 1. t^2 is in fact an 'inner function' and the 2 t comes from the Chain Rule.
We will claify this situation below.
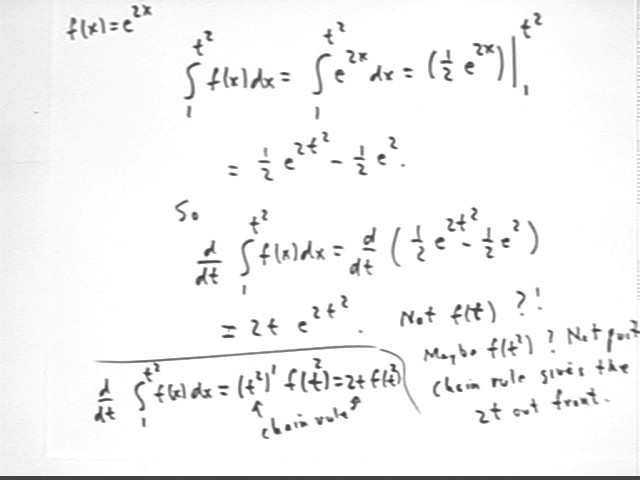
The statement d/dt [ int(f(x), x, c, t ] = f(t) is a short statement of the Second Fundamental Theorem of Calculus, which we verified in the example before last for c = 1 and f(x) = x^2.
If this statement is true then [ int(f(x), x, c, t ] must be an antiderivative of f(t). Gotta be so, since if the derivative of the expression is f(t) then the expression is an antiderivative of f(t).
Letting F(t) stand for [ int(f(x), x, c, t ] the above statements are equivalent to F ' (t) = f(t).
If F(t) = [ int(f(x), x, c, t ] then [ int(f(x), x, c, g(t) ] ) = F(g(t)). So d/dt [ int(f(x), x, c, t ] = d/dt(F(g(t)) = g ' (t) * F ' (g(t).
Since F ' (t) = f(t), F ' (g(t)) = f(g(t)) so that finally d/dt [ int(f(x), x, c, t ] = g ' (t) * F ' (g(t)).
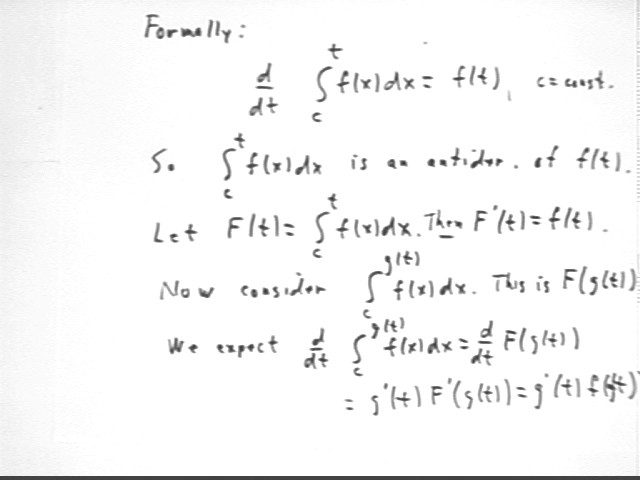
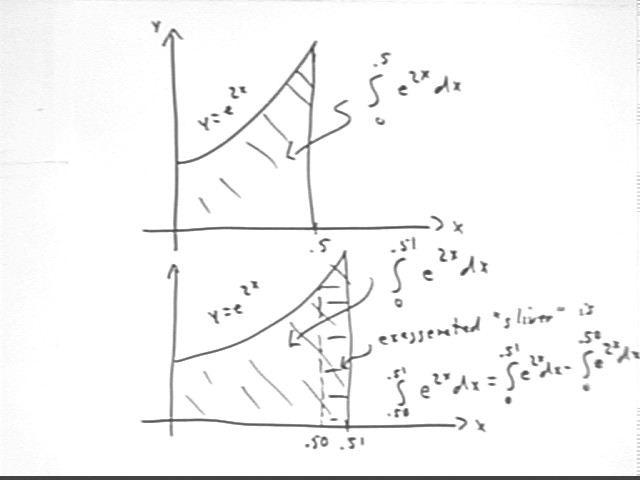
Represent the integral of e^(2x) with respect to x, from x = 0 to x = .5, as the area beneath a curve.
The integral is represented as the area beneath the y = e^(2x) graph between x = 0 and x = .5, as in the figure below.
Represent in a similar manner the integral of the same function between x = 0 and x = .51.
The integral is represented as the area beneath the y = e^(2x) graph between x = 0 and x = .51, as in the figure below.
Represent the difference between the two integrals and an area on the graph.
The difference is represented as the area beneath the y = e^(2x) graph between x = .50 and x = .51, as in the figure below.
Represent in terms of the graph the average rate at which the integral changes with respect to change in the upper limit.
The average rate at which the integral changes with respect to change in the upper limit is
ave rate = change in integral / change in upper limit
so in this case ave rate is represented by the area of the 'sliver' between x = .50 and x = .51, divided by the difference .01 between the upper limits x = .50 and x = .51. This is depicted in the figure below.
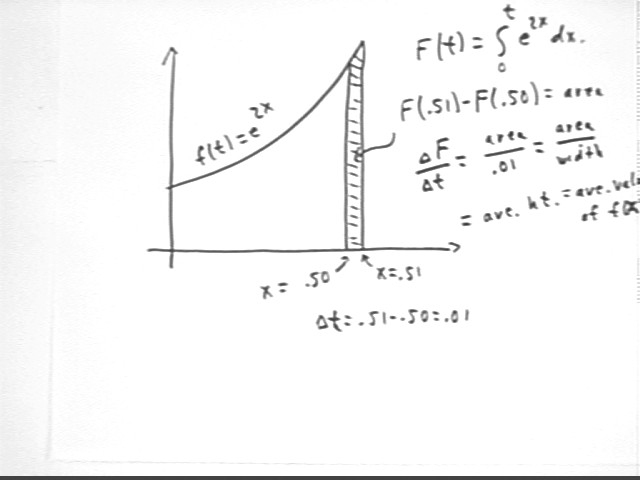
The average rate is thus
ave rate = area of 'sliver' / width of 'sliver' = ave value of f(x) = e^(2x) for x on the interval .50 < x < .51.
That is, the average rate at which the integral of e^(2x) changes, with respect to the variable of integration, is equal to the value of e^(2x).