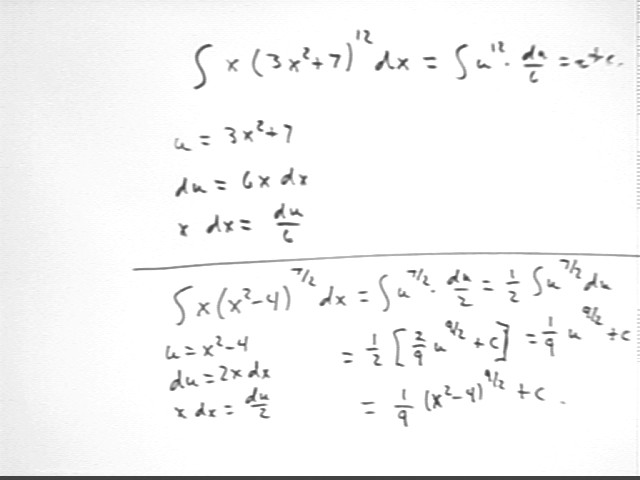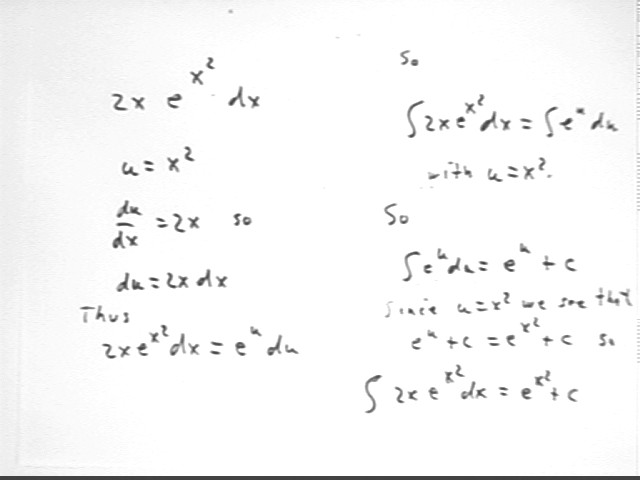
Calculus II Class 01/22
Calculus I Quiz 0122
Consider the expression 2 x e^(x^2) dx.
Let u = x^2. What is du/dx, and what then is the differential du
du/dx = d(x^2) / dx = 2 x. So du = d(x^2) = (x^2)' dx = 2x dx.
Can you find du 'hiding' in the expression 2 x e^(x^2) dx?
Sure. It's highlighted and underlined in 2x e^(x^2) dx.
Can you express 2x e^(x^2) dx in terms of u and du, with no reference to x anywhere?
Replacing the 2x dx by du and the x^2 by u we write
2x e^(x^2) dx = e^u du.
Can you integrate your expression?
Integral of e^u du is e^u + c.
Expressed in terms of x we have e^(x^2) + c.
Thus integral( 2x e^(x^2) dx ) = e^(x^2) + c.
Using the chain rule to differentiate e^(x^2) + c we can confirm that the derivative of e^(x^2) is (x^2)' * e^(x^2) = 2 x e^(x^2).
The figure below summarizes the process:
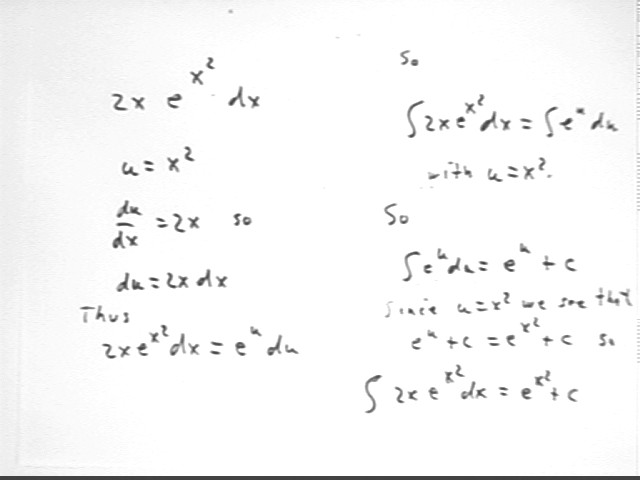
Consider the expression 6 x e^(x^2) dx.
Let u = x^2. What is du/dx, and what then is the differential du?
Can you find du 'hiding' in the expression 6 x e^(x^2) dx?
Can you express 6 x e^(x^2) dx in terms of u and du, with no reference to x anywhere?
Can you find an antiderivative for your expression?
As shown in the figure below we let u = x^2 so that du = 2x dx.
We have x dx in the expression 6 x e^(x^2) so we rearrange du = 2 x dx into the form x dx = du / 2. It is recommended that constants in the expression for du always be 'moved' to the du side in this manner.
Replacing x dx by du / 2 and x^2 by u we obtain integrand 6 e^u * du / 2 = 3 e^u du, which we easily integrate to get 3 e^u + c.
Then replacing du by x^2 we obtain our final expression 3 e^(x^2) + c.
Note how this procedure, where we allow u to stand for the inner function of a composite, can allow us to find an antiderivative in a situation involving the chain rule.
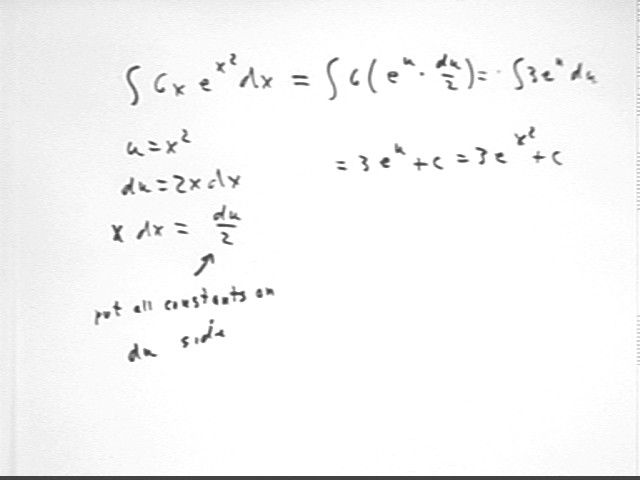
Consider the expression x^2 sin(x^3) dx.
Let u = x^3. What is du/dx, and what then is the differential du?
Can you find du 'hiding' in the expression x^2 sin(x^3) dx?
Can you express x^2 sin(x^3) dx in terms of u and du, with no reference to x anywhere?
Can you find an antiderivative for your expression?
We have seen how letting u stand for the innermost function of a composite can help us find an antiderivative. So we follow this procedure once more.
x^3 is the innermost function of the composite sin(x^3). Hopefully x^2 will be the expression we need in order to obtain our antiderivative.
Letting u = x^3 we get du = 3 x^2 dx.
Following the general idea of putting all constants on the du side we get x^2 dx = du/3.
Substituting we obtain sin(u) * du/3, leading us to 1/3 * integral( sin(u) du).
The general antiderivative of sin(u) with respect to u is - cos(u); our general antiderivative is therefore 1/3 ( -cos(u) + c) = - 1/3 cos(x^3) + c.
We can easily verify that the derivative of this result is x^2 sin(x^3).
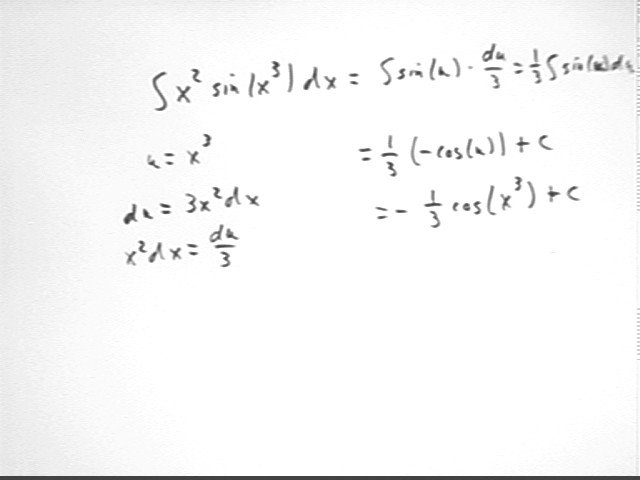
Consider the expression sin(x) e^(cos(x)) dx.
Let u = cos(x). What is du/dx, and what then is the differential du?
Can you find du 'hiding' in the expression sin(x) e^(cos(x)) dx?
Can you express sin(x) e^(cos(x)) dx in terms of u and du, with no reference to x anywhere?
Can you find an antiderivative for your expression?
Our composite this time is e^cos(x).
So we let u = cos(x), obtaining du = - sin(x) dx so that sin(x) dx = - du.
Replacing sin(x) dx with du and cos(x) with u we obtain the expressions indicated in the figure below.
Our general integral is thus - e^u + c = e^-cos(x) + c.
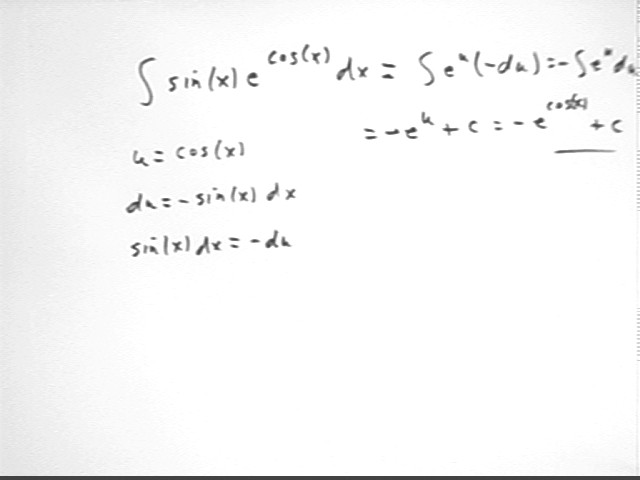
The composite in the figure below is (3x^2 + 7) ^ 12 so we let u = 3x^2 + 7.
We obtain du = 6 x dx so that x dx = du / 6.
We replace x dx with du/6 and 3x^2 + 7 with u to obtain u^12 * du / 6, which we will easily be able to integrate.
In the lower part of the figure we follow the same strategy, obtaining 1/2 integral (u^(7/2) du) with u = x^2 - 4.
The general antiderivative of the power function u^(7/2) is 2/9 u^(9/2). This leads to the solution indicated below.