Calculus II Class 02/03
Calculus I Quiz 0203
Find the following:
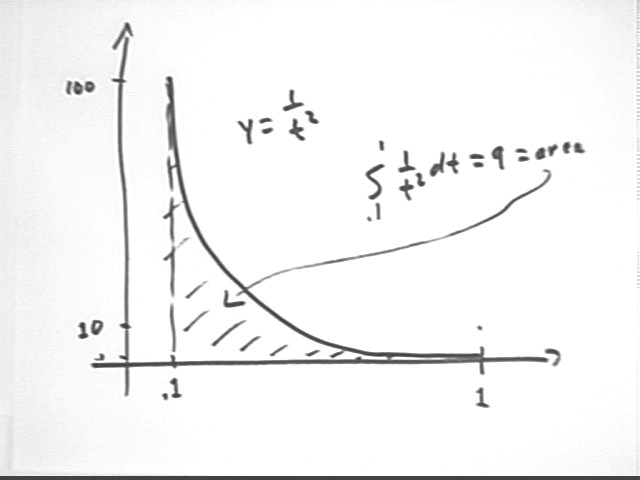
the integral from .1 to 1 of the function 1/t^2.
antiderivative of f(t) = 1 / t^2 is F(t) = -1/t.
Integral from .1 to 1 is therefore F(1) - F(.1) = -1/1 - (-1/.1) = -1 + 10= 9.
This represents the area under the y = 1/t^2 curve, from t = .1 to t = 1. The corresponding segment of the curve is concave up and decreases from the point (.1, 100) to the point (1, 1).

the integral from .01 to 1 of the function 1/t^2.
Integral from .1 to 1 is therefore F(1) - F(.01) = -1/1 - (-1/.01) = -1 + 100 = 99.
This represents the area under the y = 1/t^2 curve, from t = .01 to t = 1. The corresponding segment of the curve is concave up and decreases from the point (.01, 10,000) to the point (1, 1).
the integral from .001 to 1 of the function 1/t^2.
Integral from .001 to 1 is therefore F(1) - F(.001) = -1/1 - (-1/.001) = -1 + 1000 = 999.
This represents the area under the y = 1/t^2 curve, from t = .001 to t = 1. The corresponding segment of the curve is concave up and decreases from the point (.001, 1,000,000) to the point (1, 1).
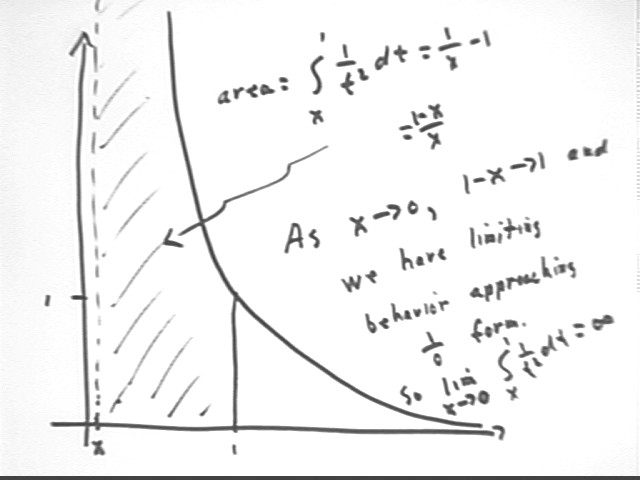
the integral from x to 1 of the function 1/t^2.
Integral from x to 1 is F(1) - F(x) = -1/1 - (-1/x) = -1 + 1/x = 1/x - 1 = (1-x) / x.
This represents the area under the y = 1/t^2 curve, from t = x to t = 1. The corresponding segment of the curve is concave up and decreases from the point (x, 1/x^2) to the point (1, 1).
the limiting value of the integral from x to 1 of the function 1/t^2, as x approaches 0.
The integral is (1-x) / x, which as x -> 0 approaches form 1 / 0, indicating that the integral approaches infinity.
This means that if we let x be close enough to zero, the integral can exceed any bound we wish to specify. We can get as much area as we like by letting x be sufficiently close to zero.
Find the following:
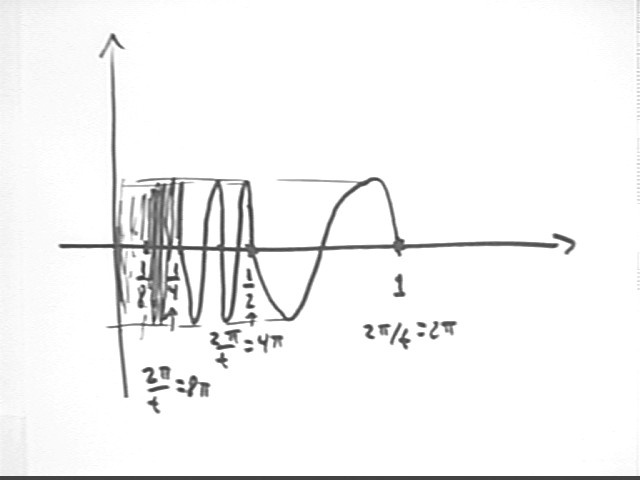
the integral from .1 to 1 of the function sin(2 pi/t).
You can't find an antiderivative in closed for; no such closed form exists for this funciton.
This function goes through a complete cycle every time 2 pi / t changes by 2 pi.
Between t = 1/2 and t = 1 we see that 2 pi / t changes from 4 pi to 2 pi, so that the sine function goes through a complete cycle between t = 1/2 and t = 1.
Between t = 1/4 and t = 1/2 we see that 2 pi / t changes from 8 pi to 4 pi, so that the sine function goes through two complete cycles between t = 1/4 and t = 1/2.
Between t = 1/8 and t = 1/4 we see that 2 pi / t changes from 16 pi to 8 pi, so that the sine function goes through two complete cycles between t = 1/8 and t = 1/4.
The function will go through increasing numbers of cycles every time we move twice as close to t = 0.
Without an antiderivative function it will be difficult to even approximate the function. However we can see that as we move toward t = 0 we will be accumulating first positive, then negative, then positive, then negative 'areas'. We also note that the 'areas' are increasingly 'bunched up'.
For example the first positive 'hump we encounter as we move inward from t = 1 toward t = 0 will have greater area than the negative hump we encounter next, so that the total area between t = 1/2 and t = 1 is positive.
This pattern will continue, so that the total area from t = 1/4 to t = 1 will also be positive, the same being true from t = 1/8 to t = 1, etc..
The changes to total area become smaller and smaller as we approach t = 0, so that it is conceivable that as we approach t = 0 the total area will remain positive, and even that the area might approach a definite limit.
Find the following:
the integral from .1 to 1 of the function sin(2 pi/t) / t^2.
As seen in the figure below, substitution u = 2 pi / t leads us to the antiderivative
1 / (2 pi) * cos(2 pi / t)
and then to
the integral
integral from .1 to 1 = 1 / (2 pi) - 1 / (2 pi ) * cos(2 pi / .1) = 1 / (2 pi) - 1 / (2 pi) cos(20 pi) = 1 / (2 pi ) - 1 / (2 pi) = 0.

the integral from .011 to 1 of the function sin(2 pi/t) / t^2.
this time we get the integral
integral from .011 to 1 = 1 / (2 pi) - 1 / (2 pi ) * cos(2 pi / .011) = .02526.
the integral from .00111 to 1 of the function sin(2 pi/t) / t^2.
.02986
the integral from x to 1 of the function sin(2 pi/t) / t^2.
the limiting value of the integral from x to 1 of the function sin(2 pi/t) / t^2, as x approaches 0.
Does the result keep fluctuating or does it start behaving in such a way that we do indeed get a limit?
Numerical investigation is unclear.
Evaluating the integral from x to 1, where r is a number randomly chosen between 0 and .001, we obtain the 10 independent approximations
[0.3171127837иа, 0.3182710884иа, 0.1652621899иа, 0.3030351283иа, 7.807219778и10^(-5)иа, 0.06973724302иа, 0.1024165720иа, 0.07004683819иа, 0.005858130770иа, 0.2095058782иа]
Evaluating the integral from x to 1, where r is a number randomly chosen between 0 and .0001, we obtain the 10 independent approximations
[0.1101555912иа, 0.1682873510иа, 0.1498065854иа, 0.3126104225иа, 0.3182356389иа, 0.2412006316иа, 0.0001252991626иа, 0.08115387800иа, 0.1451588705иа, 0.0005000701483иа]
Evaluating the integral from x to 1, where r is a number randomly chosen between 0 and .00001, we obtain the 10 independent approximations
[0.2835872881иа, 0.09623582042иа, 0.2999309078иа, 0.06400698490иа, 0.3086687079иа, 0.09281689440иа, 0.1521736411иа, 0.01831385277иа, 0.0001208367561иа, 0.01437561392иа]
Evaluating the integral from x to 1, where r is a number randomly chosen between 0 and .000001, we obtain the 10 independent approximations
[0.04216500802иа, 0.1718963955иа, 0.1273198651иа, 0.1273198651иа, 0.07285608983иа, 0.2397056683иа, 0.2407286156иа, 0.02464787576иа, 0.3156210409иа, 0.07419431375иа]
Evaluating the integral from x to 1, where r is a number randomly chosen between 0 and .001, we obtain the 10 independent approximations
[0.3111242027иа, 0.06226755250иа, 0.3176568030иа, 0.1444699775иа, 0.2200609029иа, 0.04805001349иа, 0.1502310542иа, 0.1539475393иа, 0.3137846479иа, 0.1040687025иа]
It is notable that none of the approximations is negative and that there is no consistency to the results. It is conceivable that no matter how close we place r to zero, the value of the integral will be unpredictable.
It would then follow that as we allow x to approach zero, the integral of this function from x to 1 will still tend to fluctuate pretty randomly between 0 and at least .3.
Note that these are 10-significant-figure approximations made by DERIVE. It is conceivable that the fluctuations observed are the result of the nature of the approximation scheme used by that program rather than the actual behavior of the functoin.
Find the following:
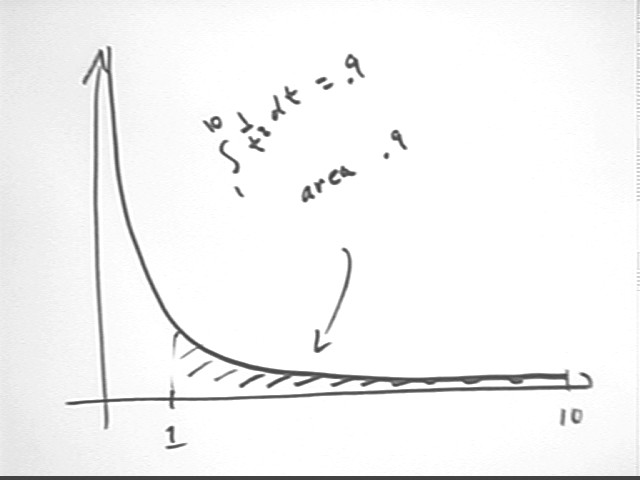
the integral from 1 to 10 of the function 1 / t^2.
The antiderivative F(t) = - 1 / t gives us
F(10) - F(1) = -1/10 + 1 = .9.
the integral from 1 to 100 of the function 1 / t^2.
The antiderivative F(t) = - 1 / t gives us
F(100) - F(1) = -1/100 + 1 = .99.
the integral from 1 to 1000 of the function 1 / t^2.
The antiderivative F(t) = - 1 / t gives us
F(1000) - F(1) = -1/1000 + 1 = .999.
Bigger and bigger 'jumps' in the upper limit result in smaller and smaller change in the integral. Looks like as the upper limit approaches infinity the integral will converge to 1.
the integral from 1 to x of the function 1 / t^2.
The antiderivative F(t) = - 1 / t gives us
F(x) - F(1) = -1/x + 1 .
As x gets larger and larger, -1/x approaches zero and our integral approaches 0 + 1 = 1.
the limiting value of the integral from 1 to x of the function 1 / t^2, as x approaches infinity.
 \
\
Sketch the graph of y = 1 / (t - 2)^2 from t = 0 to t = 4.
Find the integral of y = 1 / (t - 2)^2 from t = 1 to t = 3.
Find the integral of y = 1 / (t - 2)^2 from t = 0 to t = 4.
Do your results agree with your picture (look at the area under the curve for each interval)? If not, what's wrong here?