Calculus II Class 02/05
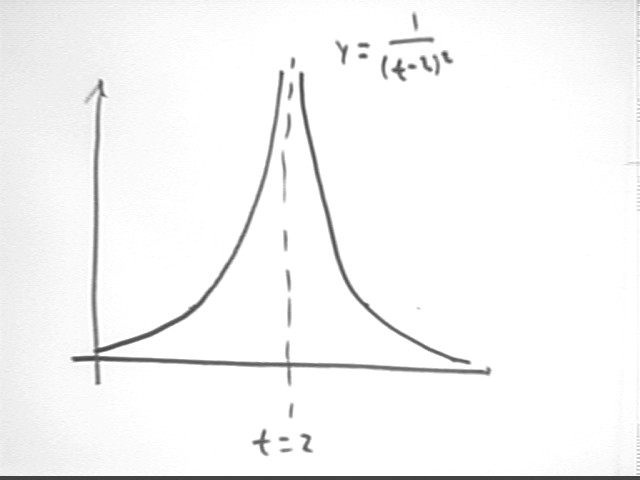
Sketch the graph of y = 1 / (t - 2)^2 from t = 0 to t = 4.
Find the integral of y = 1 / (t - 2)^2 from t = 1 to t = 3.
Find the integral of y = 1 / (t - 2)^2 from t = 0 to t = 4.
Do your results agree with your picture (look at the area under the curve for each interval)? If not, what's wrong here?
Among other things the graph of y = 1 / (t-2)^2 is positive for all t > 0 for which the expression is defined. The graph also has a vertical asymptote at x = 2 and horizontal asymptote at both the positive and negative x axes.

Antiderivative of f(t) = 1 / (t-2)^2 is easily found by the substitution u = t - 2 to be F(t) = -1 / (t - 2).
The integral of f(t) from t = 1 to t = 3 is therefore F(3) - F(1) = -1 / (3-2) - ( -1 / (1-2) ) = -1 - 1 = -2.
The integral of f(t) from t = 0 to t = 4 is therefore F(4) - F(0) = -1 / (4-2) - ( -1 / (0-2) ) = -1/2 - 1/2 = -1.
Neither of these results makes any sense.

The key is that the function has a vertical asymptote at t = 2, and is therefore not defined through either of the intervals t = 1 to t = 3 or t = 0 to t = 4.
To integrate we have to integrate everything to the left of t = 2, then everything to the right of t = 2.

For an important contrast note that the integral shown below converges. You should check this out by performing the indicated integrals and taking the limits.
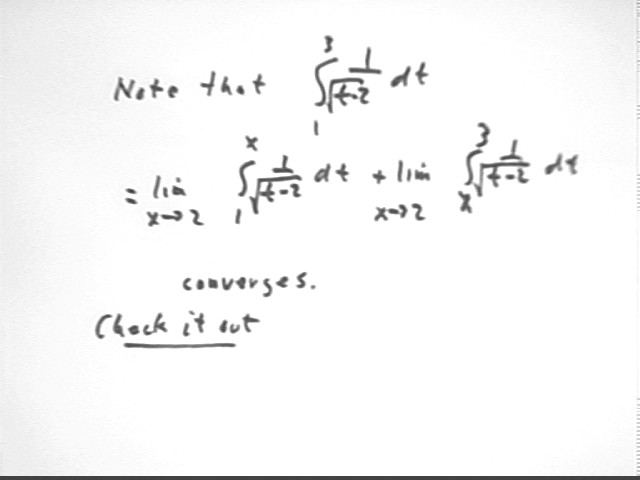
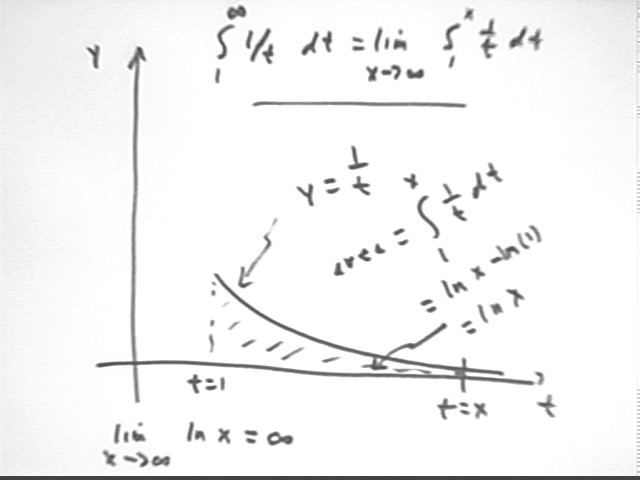
Does the integral from t = 1 to infinity of y = 1 / t converge or diverge? Hint: Look at the limiting value of the integral from 1 to x, as x -> infinity.
integral (1/t, t, 1, infinity) = lim(x -> infinity) integral(1/t, t, 1, x) = lim(x -> infinity) ( ln x - ln 1) = lim (x -> infinity) (ln x).
If ln x is bounded as x -> infinity then there would be some number N which ln x cannot exceed. In this case we would have
ln x < N for all x.
But this is the same as saying that x < e^N for all x. But this cain't be since x = e^N + 1, for example, is a perfectly good number which is bigger than e^N.
It follows that our integral is divergent.
Does the integral from t = 1 to infinity of y = 1 / t^1.01 converge or diverge? Hint: Look at the limiting value of the integral from 1 to x, as x -> infinity.
Antiderivative of 1 / (t^1.01) = t^-1.01 is the antiderivative of t^n, which is 1 / (n+1) t^(n+1), with n = 1.01. So we get antiderivative F(t) such that
F(t) = 1 / (1 - 1.01) * t^(-1.01 + 1) = -100 t^-.01 = -100 / t^.01.

In general if q is a positive number, intended here to be thought of as a small positive number, then the integral of 1 / (t + q) from t = 1 to infinity is 1/q, as shown below.
So for example if q = .01, 1 / (t+q) = 1 / (t+.01) and the integral will be 1 / q = 100.
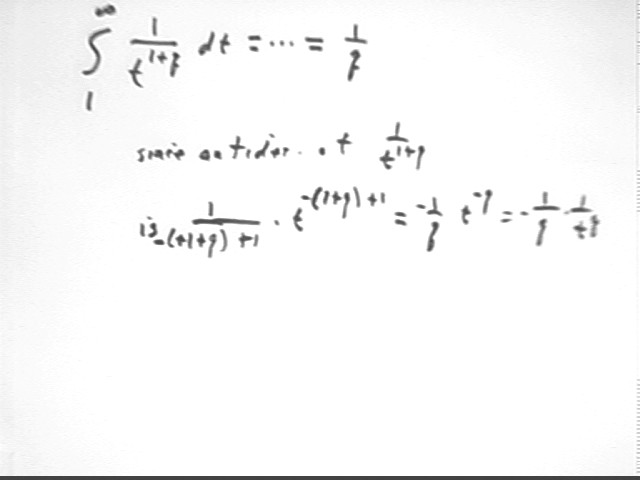
Our general result is that when integrating from 1 to infinity:

Does the integral from t = 0 to infinity of y = e^-.003 t converge or diverge? Hint: Look at the limiting value of the integral from 1 to x, as x -> infinity.
This problem was not done in class but is easily solved.
We will use antiderivative F(t) = -1 / (.003) e^(-.003 t) = -1000 / 3 * e^(-003 t).
The integral of f(t) = e^-.003 t from 1 to x is therefore F(x) - F(1) = -1000/3 e^(-.003 x) - (-1000/3 * e^(-.003 * 1) = -1000/3 e^(-.003 x) + 1000/3 * e^-.003.
As x -> infinity, e^(-.003 x) = 1 / e^(.003 x) approaches zero, due to the eventually unlimited growth of the e^(.003 x) in the denominator.
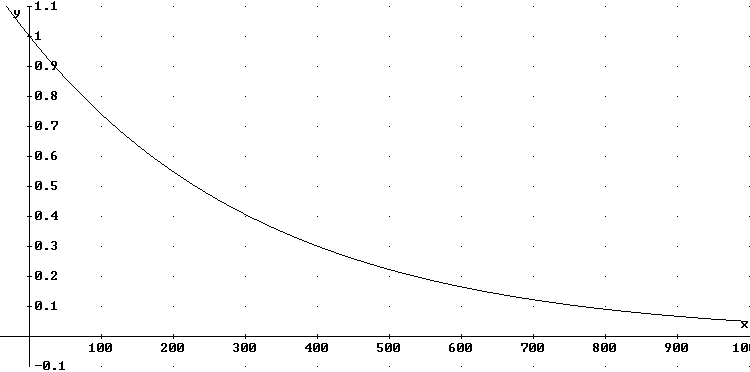
We find the limit of the integral as t -> infinity to therefore be limit{x -> infinity) [ -1000/3 e^(-.003 x) + 1000/3 * e^-.003 ] = 0 + 1000/3 * e^-.003, or approximately 334.3.
The plot below shows the graph of this function from t = 0 to t = 1000. A reasonable estimate of the average 'height' of the graph is .3 so a reasonable estimate of the area beneath the curve is .3 * 1000 = 300. It is not unreasonable to expect that the 'rest of the graph', from t = 1000 on, contains total area around 30 and makes the preceding result 334.3 for the total area very plausible.
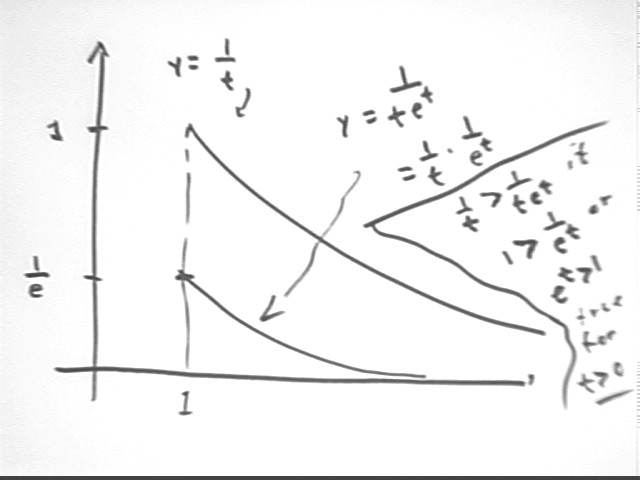
For t > 1 how does the graph of y = 1 / (t * e^t) compare with the graph of y = 1 / t and the graph of 1 / t^1.01? What does this comparison tell you about the convergence or divergence of y = 1 / (t * e^t)?
For t > 1 the graph of 1 / (t e^t) lies always below the graph of 1 / t, as indicated below. We observe the following:
The integral from 1 to infinity of 1/t diverges. That area grows beyond all bounds as we move to the right.
If another graph lies always above the graph of 1/t then it will contain an area that grows beyond all bounds and its integral will also diverge.
If another graph lies always below the graph of 1/t then might possibly diverge, but we don't know for sure because lots of convergent functions (e.g, 1/t^2) will lie below the graph of 1/t.
So we can't draw any conclusions from this comparison of 1/(t e^t) with 1/t.
However comparing 1 / (t e^t) with 1 / t^1.01 we first note that if 1 / (t e^t) lies lower than the convergent 1 / t^1.01, then since the graph of the convergent 1 / t^1.01 can't 'contain' an infinite area, the integral of 1 / (t e^t) must converge.
The inequality 1 / (t e^t) < 1 / t^1.01 gives us t^.01 < e^t. This is true for t = 1, since 1 < e, and since e^t grows faster than any power function (remember l'hopital) the inequality will hold for all t > 1.
It follows that the integral from 1 to infinity of 1 / (t e^t) converges.
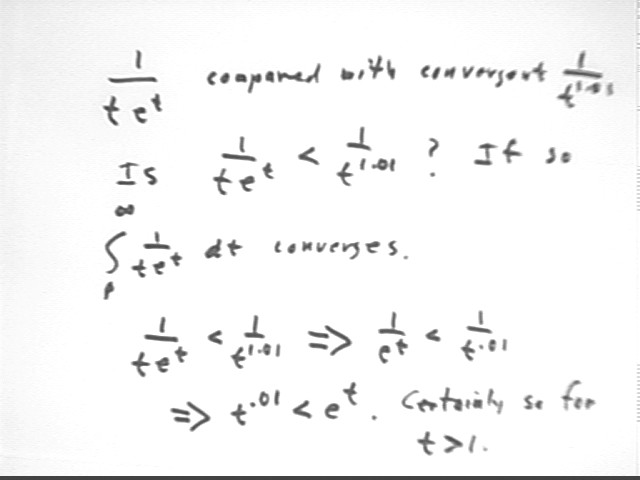
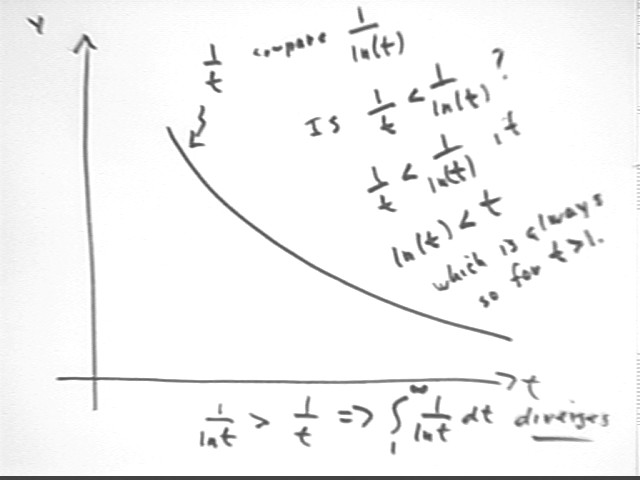
For t > 1 how does the graph of y = 1 / ln(t) compare with the graph of y = 1 / t and the graph of 1 / t^1.01? What does this comparison tell you about the convergence or divergence of y = 1 / ln(t)?
The graph of y = 1/t is sketched below. The graph of 1 / ln(t) is not sketched, but we see that 1/t < ln(t) whenever ln(t) < t, which is true for any t > 1.
Since the graph of 1 / ln(t) for 1 < t 'lies above' the graph of 1/t, which diverges to infinity, we see that the integral of 1 / ln(t) must be greater than the divergent integral of 1 / t and that the integral of 1 / ln(t), t from 1 to infinity, must diverge.
Question posed by class: How do we integrate cos(sqrt(x)) / sqrt(x).
This situation involves the composite function cos(sqrt(x)). So our first attempt will be to set u equal to the inner function and see if the substitution works.
We find the the 1 / sqrt(x) dx present in the integral is equal to du / 2, so the integration proceeds easily.
Our general result will be sin(u) / 2 + c = sin(sqrt(x)) / 2 + c.
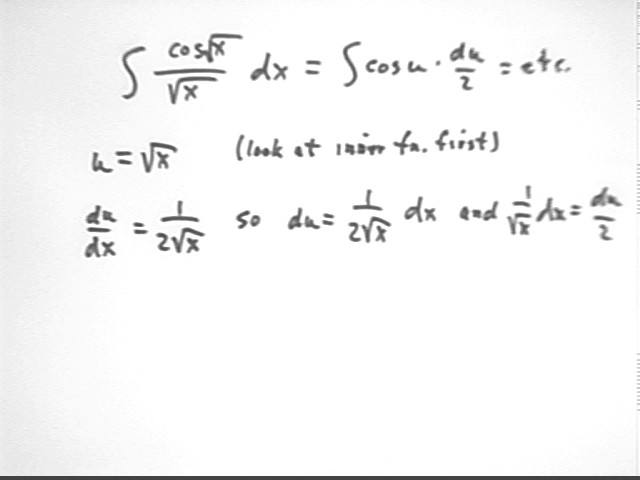
First thing to try for substitution, which 'undoes' composites:
1. Look for the inner function of a composite. Try u = that function.
2. Figure out du/dx, then du.
3. Get constants over there with the du.