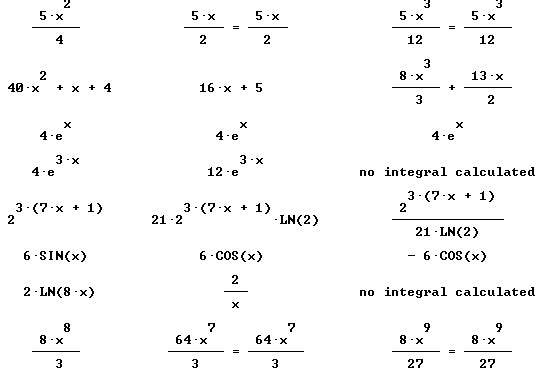Calculus II Class 02/12
The picture below shows a marble being held in a track.

An end view shows how the marble extends about half a radius down into the groove of the track.
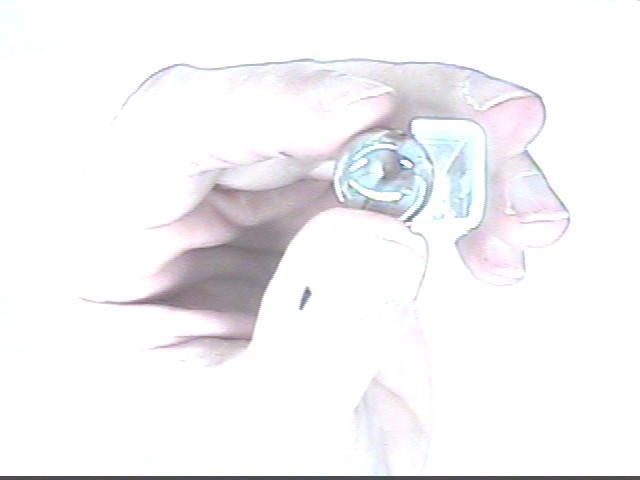
The figure below illustrates how we can determine how far down into the track the marble extends.
The marble, of radius 1.565 cm, is shown resting on a track of width 1.27 cm.
The distance d to which the marble extends down into the track is indicated.
We cannot find d directly but we can construct a right triangle from the center of the circle to the point where the circle touches the track, with one side vertical and the other horizontal. We easily determine that the hypotenuse is the radius 1.56 cm / 2 = .78 cm and the horizontal leg is 1.27 cm / 2 = .63 cm, both results rounded to 2 significant figures.
The triangle is easily solved to find that its vertical leg is .30 cm. It follows easily that d = .78 cm - .30 cm = .40 cm.
Note that if the marble was cut horizontally at the level of the track, the cross-section of the cut would be a circle with radius .63 cm.

The figure below shows that if the marble was cut at height h above its lowest point the radius r of the cut would be the horizontal leg of a right triangle whose hypotenuse is .78 cm and whose other leg is .78 cm - h.
The Pythagorean Theorem tells us that the radius is therefore r = sqrt((.78 cm)^2 - (.78 cm - h)^2 ) = ... = sqrt( 1.56 h - h^2).
It follows that the cross-sectional area of a horizontal 'cut' made at height h above the lowest point is pi r^2 = ... = pi ( 1.56 h - h^2).
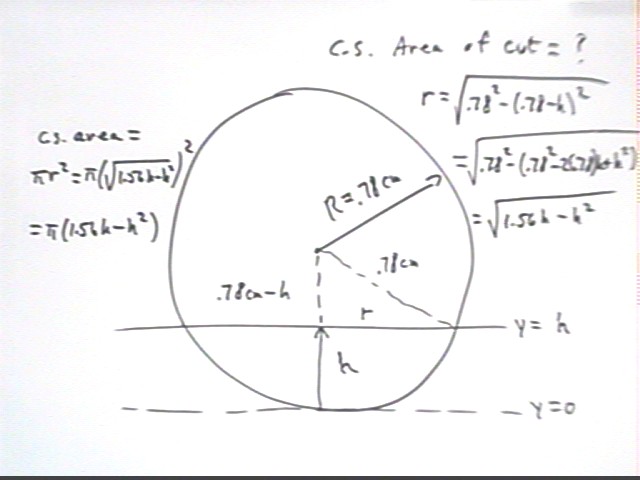
The graph done in class was labeled the same as the graph below but graph 'altitudes' were incorrect. The correct graph is shown below.
This graph shows cross-sectional area vs. height h.
We easily find that the numerical trapezoidal areas are .023, .066 and .102.
The units of graph altitude and width are respectively cm^2 and cm, leading to units cm^3 for the quantity represented by graph area.
Thus the trapezoidal areas represent .023 cm^3, .066 cm^3 and .102 cm^3.
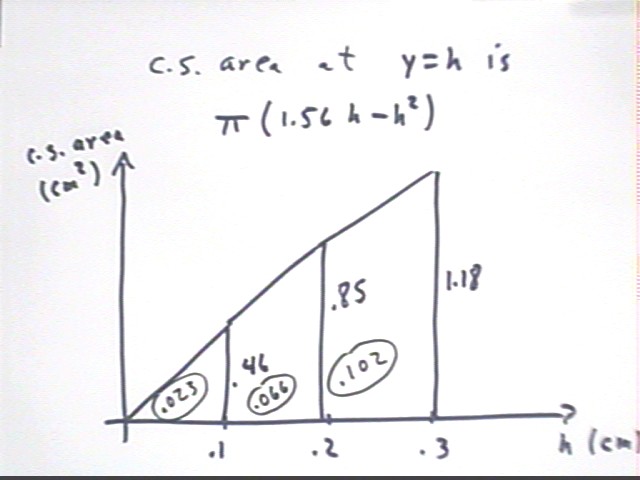
We interpret trapezoidal areas:
A trapezoidal area is ave altitude * width.
Ave altitude represents approximate average cs area (just look at the label of the vertical axis).
Width represents change in h (look at the label of the horizontal axis).
For example ave altitude of the second trapezoid is .66, representing an ave cross sectional area of .66 cm^2. Width of the second trapezoid is .1, representing the .1 cm change in h between h = .1 and h = .2.
The area of the trapezoid is therefore .66 cm^2 * .1 cm = .066 cm^3.
This tells us that the slice pictured below, lying between h = .1 and h = .2 and with ave cs area approximately .66 cm^2, has thickness .1 cm and therefore approx. volume .66 cm^2 * .1 cm = .066 cm^3.
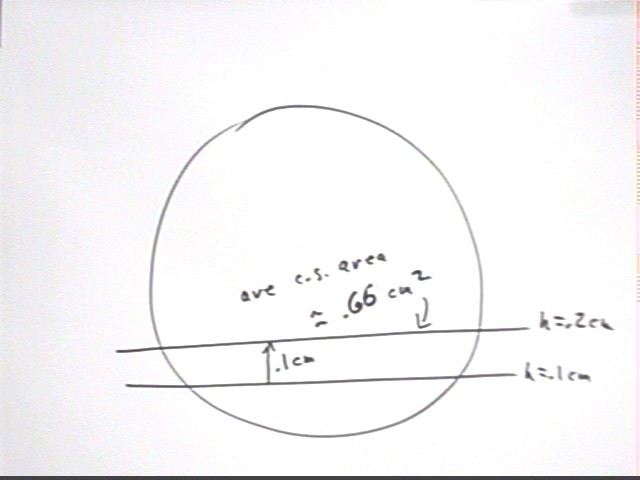
This illustrates why the trapezoidal areas correspond to the approximate volumes of slices of the sphere.
The graph depicted below could be broken into trapezoids and would indicate cross-sectional areas from h = 0 thru h = 1.5. This graph would be the same as that shown previously, except that the former graph extended only to h = .3.
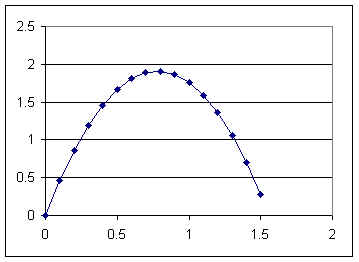
The table below summarizes the information we would get form this graph, representing slice areas from h = 0 to h = 1.5 cm. This takes us from the lowest point of the marble almost to the highest (recall that the diameter of the marble is about 1.57 cm).
The table shows
the area of the cross section of each cut, calculated by solving the right triangle appropriate to the height h at which the cut is made
the trapezoidal average area of the slice, obtained by averaging the cross sectional areas of the cuts at the bottom and the top of each slice. Note that this is only a trapezoidal approximation to the average area of the slice.
the area of the trapezoid on the graph, which represents the volume of the corresponding slice
| h | r | area of c.s. of cut | trapezoidal ave slice area | trapezoidal graph area |
| 0 | 0 | 0 | ||
| 0.1 | 0.382099463 | 0.4586736 | 0.2293368 | 0.02293368 |
| 0.2 | 0.521536192 | 0.8545152 | 0.6565944 | 0.06565944 |
| 0.3 | 0.614817046 | 1.1875248 | 1.02102 | 0.102102 |
| 0.4 | 0.681175455 | 1.4577024 | 1.3226136 | 0.13226136 |
| 0.5 | 0.728010989 | 1.665048 | 1.5613752 | 0.15613752 |
| 0.6 | 0.758946638 | 1.8095616 | 1.7373048 | 0.17373048 |
| 0.7 | 0.77588659 | 1.8912432 | 1.8504024 | 0.18504024 |
| 0.8 | 0.779743548 | 1.9100928 | 1.900668 | 0.1900668 |
| 0.9 | 0.770713955 | 1.8661104 | 1.8881016 | 0.18881016 |
| 1 | 0.748331477 | 1.759296 | 1.8127032 | 0.18127032 |
| 1.1 | 0.71133677 | 1.5896496 | 1.6744728 | 0.16744728 |
| 1.2 | 0.657267069 | 1.3571712 | 1.4734104 | 0.14734104 |
| 1.3 | 0.581377674 | 1.0618608 | 1.209516 | 0.1209516 |
| 1.4 | 0.473286383 | 0.7037184 | 0.8827896 | 0.08827896 |
| 1.5 | 0.3 | 0.282744 | 0.4932312 | 0.04932312 |
| 1.971354 |
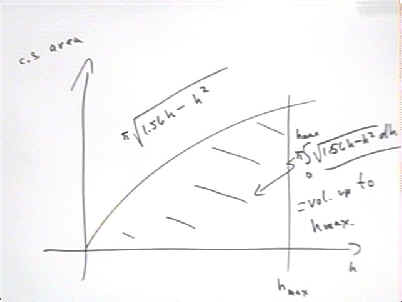
The preceding discussion shows us how the graph of cross-sectional area vs. vertical position gives us the corresponding volume of the corresponding part of the sphere.
Since the graph is defined by the function c.s. area = pi * (1.56 h - h^2), incorrectly labeled in the two figures below as pi * sqrt(1.56 h - h^2), it follows that the volume of the sphere is obtained by integrating this function from h = 0 to the maximum h.

The integral does work out (if we include pi in the integral) to duplicate the result we get from the formula V = 4/3 pi r^3 for the volume of a sphere.
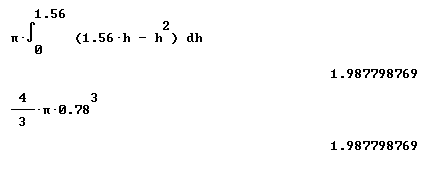
Find the derivative of each of the following:
y = x^2 e^x
y = sqrt(sin(t))
y = e^x / cos(x)
y = cos(t^2)
y = e^(x^3)
y = x^3 e^x
y = ln(sqrt(x))
y = e^-(x^2)
Does each of the following look like a substitution situation or an integration by parts situation, both or neither? Specify the substitution or breakdown into u and dv you would use for each:
integral(e^x / (e^x + 2), x)
integral((1 + ln(x)) / ( x ), x)
integral(x^2 e^-x, x)
integral(t^2 ( t^3 - 4)^3, t)
integral(x^2 / (x^2 - 1), x)
integral(sin(x) / ( (cos^2(x) + 4 cos(x) - 1), x)
integral(sin(t) / e^t, t)
integral(t^2 / (t^3 + 7)^(3/5), t )
integral(x^3 cos(x^2) sin(x^2), x)
integral(sec^2(t) e^tan(t),t)
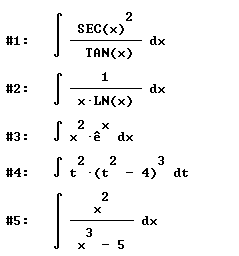
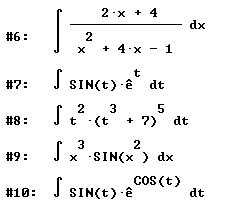
We integrate 1 / [ (x-2)(x+5) ] using partial fractions:
Express A / (x-2) + B / (x+5) as a single fraction, with a single numerator and a single denominator.
If 1 / [ (x-2)(x+5) ] = A / (x-2) + B / (x+5) then what are the values of A and B?
With 1 / [ (x-2)(x+5) ] expressed in the form A / (x-2) + B / (x+5) , what is the integral of the expression with respect to x?
We integrate 1 / [ (x-2)(x^2+5) ] using partial fractions:
Express A / (x-2) + ( B x + C) / (x^2+5) as a single fraction, with a single numerator and a single denominator.
If 1 / [ (x-2)(x^2+5) ] = A / (x-2) + ( B x + C) / (x^2+5) then what are the values of A and B?
With 1 / [ (x-2)(x^2+5) ] expressed in the form A / (x-2) + ( B x + C) / (x^2+5) , what is the integral of the expression with respect to x?
Check out the assertion made last time that integral (1 / sqrt(t-2), t, 1, 3) does indeed converge.
Find the derivative of each of the following:
y = e^x * (x^3)
y = x^(3 e^x)
y = ln x * sqrt(x)
y = e^x -(x^2)
y = e^(2x)
y = sqrt(t) sin(t)
y = e^(x / cos(x))
y = cos(t) * t^2
Does each of the following look like a substitution situation or an integration by parts situation, both or neither? Specify the substitution or breakdown into u and dv you would use for each:
integral(sec^2(x) / tan(x), x)
integral(1 / ( x ln(x)), x)
integral(x^2 e^x, x)
integral(t^2 ( t^2 - 4)^3, t)
integral(x^2 / (x^3 - 5), x)
integral((2x + 4) / (x^2 + 4 x - 1), x)
integral(sin(t) e^t, t)
integral(t^2 (t^3 + 7)^5, t )
integral(x^3 sin(x^2), x)
integral(sin(t) e^cos(t),t)
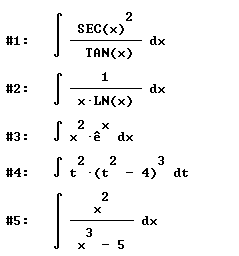
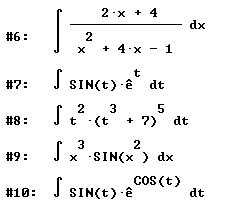
We integrate 1 / [ (x-2)(x+5) ] using partial fractions:
Express A / (x-2) + B / (x+5) as a single fraction, with a single numerator and a single denominator.
If 1 / [ (x-2)(x+5) ] = A / (x-2) + B / (x+5) then what are the values of A and B?
With 1 / [ (x-2)(x+5) ] expressed in the form A / (x-2) + B / (x+5) , what is the integral of the expression with respect to x?
We integrate 1 / [ (x-2)(x^2+5) ] using partial fractions:
Express A / (x-2) + ( B x + C) / (x^2+5) as a single fraction, with a single numerator and a single denominator.
If 1 / [ (x-2)(x^2+5) ] = A / (x-2) + ( B x + C) / (x^2+5) then what are the values of A and B?
With 1 / [ (x-2)(x^2+5) ] expressed in the form A / (x-2) + ( B x + C) / (x^2+5) , what is the integral of the expression with respect to x?
Check out the assertion made last time that integral (1 / sqrt(t-2), t, 1, 3) does indeed converge.
For t > 1 how does the graph of y = 4 / (t-.5)^2 compare with the graph of y = 1 / t and the graph of 1 / t^1.01? What does this comparison tell you about the convergence or divergence of y = 4 / (t-.5)^2?
Quickly find antiderivatives for all the functions shown below:
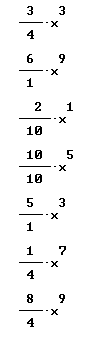

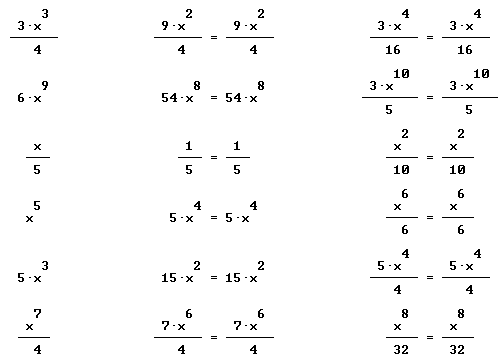
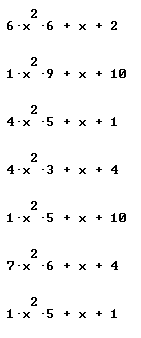
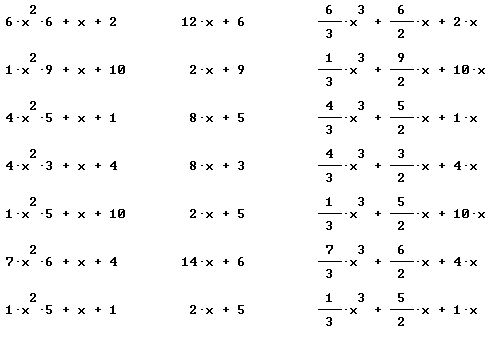
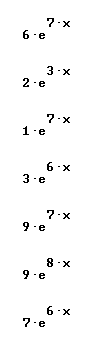
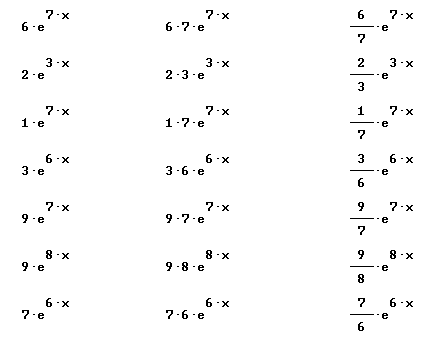
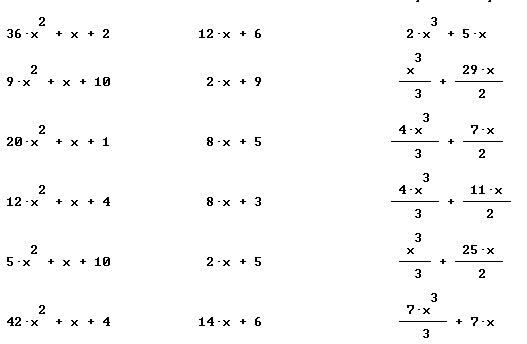
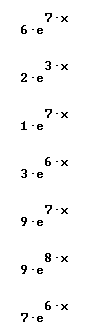
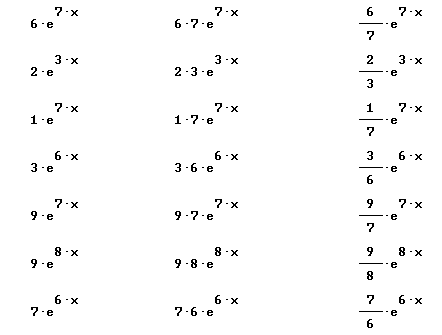
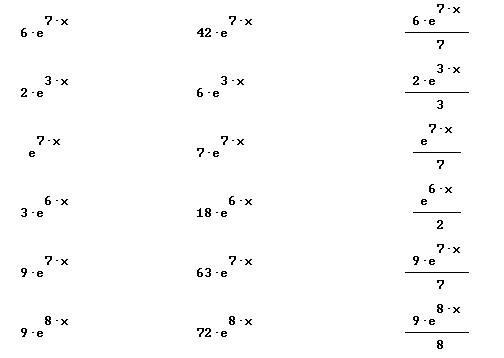
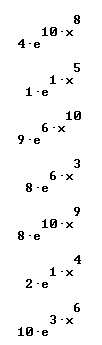


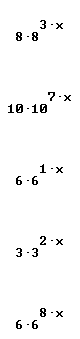
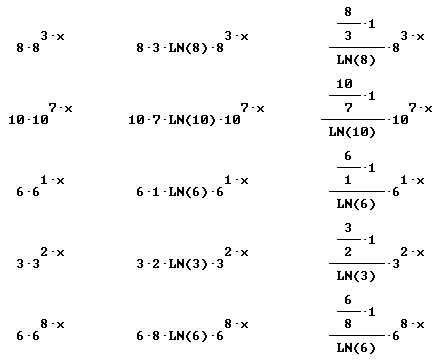
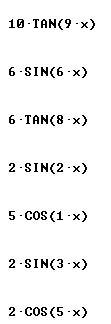
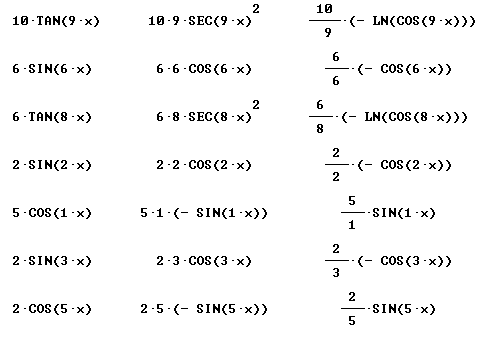
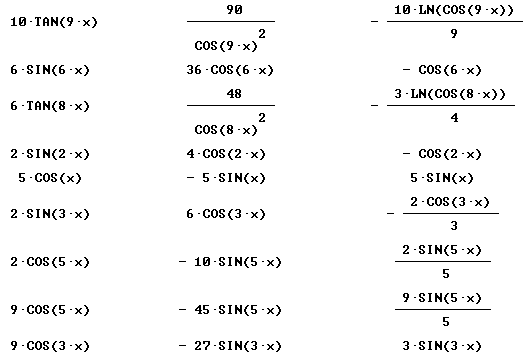
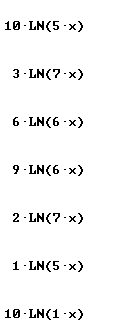
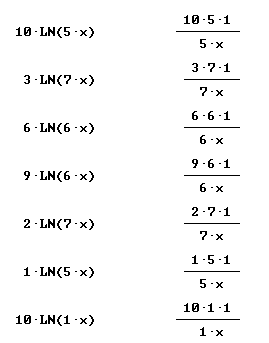

Find derivative and simples antiderivative of each:
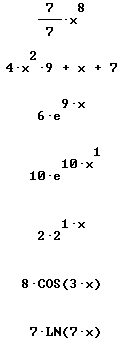
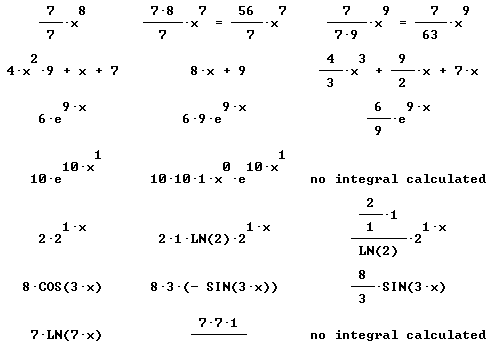
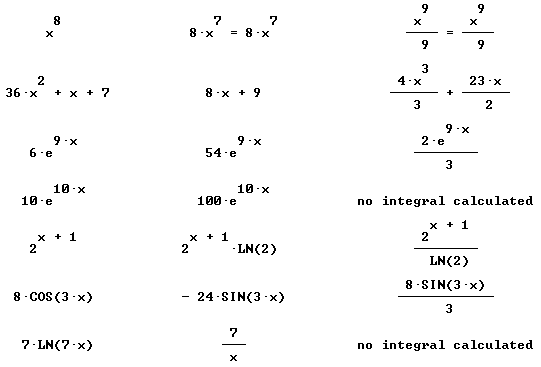
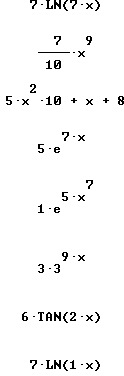
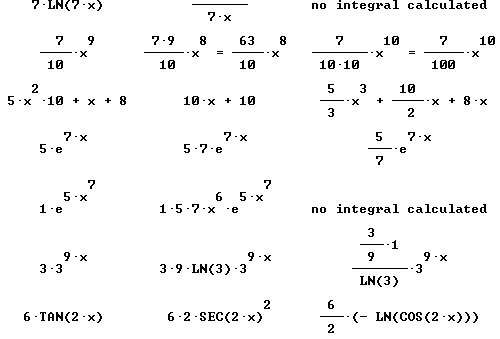
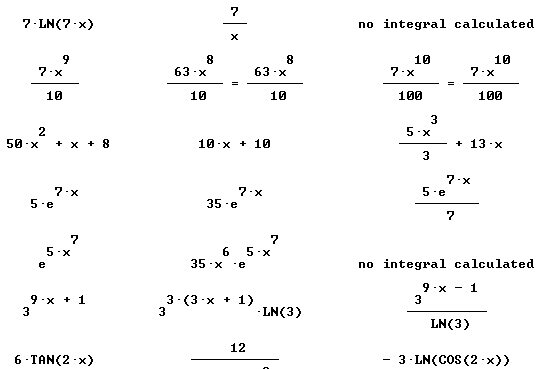
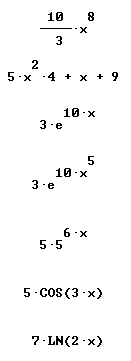
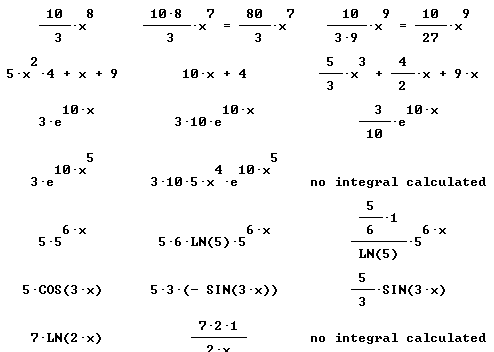
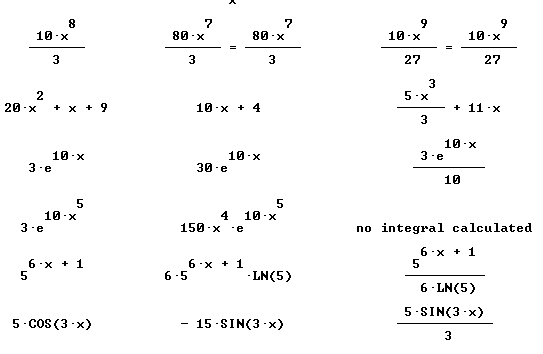
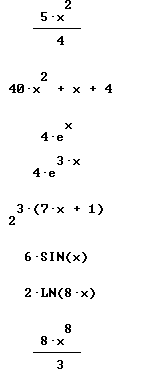
Only simplified final forms are given here: