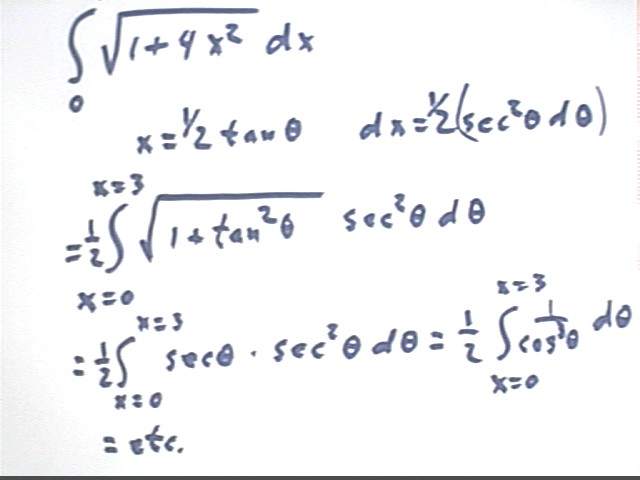Calculus II Class 02/21
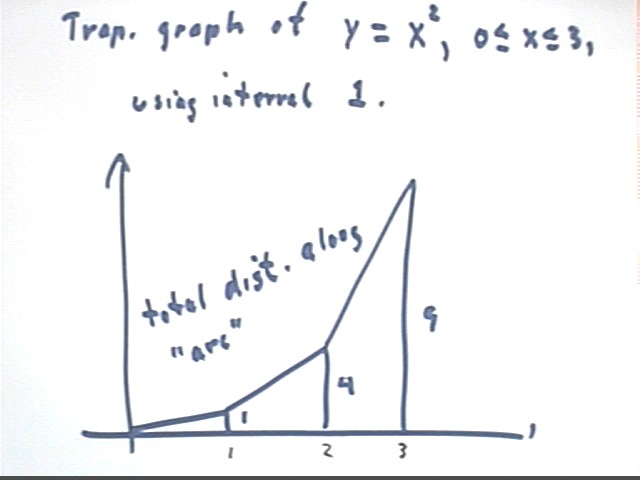
Construct a trapezoidal approximation graph for y = x^2 between x = 0 and x =
3, with increment 1. Find the total distance along the 'arc' of this
graph.
The 'arc; of the graph of y = x^2 between x = 0 and x = 3 is approximated by
the total length of the 'slope lines' at the tops of the trapezoids.
- For each 'slope line' we easily find the rise and the run.
- Knowing the rise and the run we easily find the length of the line, using
the Pythagorean Theorem.
We obtain the following specific results:
- For the first trapezoid the run is 1 and the rise is 1 - 0 = 0 so the
length of the slope line is sqrt( 1^2 + 1^2) = sqrt(2) = 1.4 approx.
- For the second trapezoid the run is 1 and the rise is 4 - 1 = 3 so
the length of the slope line is sqrt( 1^2 + 3^2) = sqrt(10) = 3.2 approx.
- For the third trapezoid the run is 1 and the rise is 9 - 4 = 5 so the
length of the slope line is sqrt( 1^2 + 5^2) = sqrt(26) = 5.1 approx.
The total arc distance is therefore about 1.4 + 3.2 + 5.1 = 9.7.
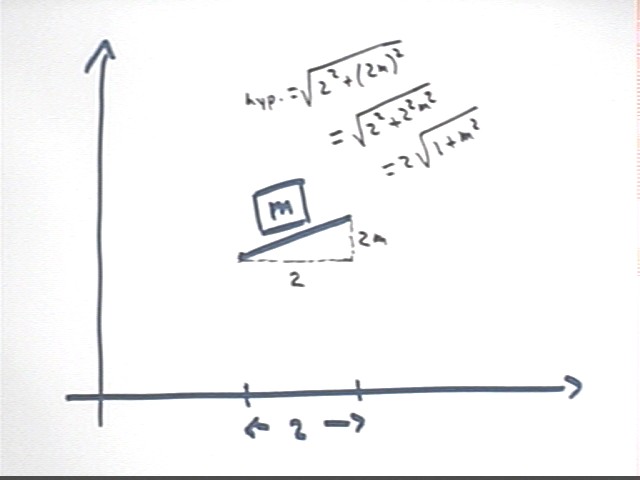
Find the length of a 'slope segment' corresponding to slope m on a
trapezoid of width 2.
We again find the rise and the run of the 'slope segment', which is shown
below.
- The run is the width 2 of the trapezoid.
- The rise is `dy = m * `dx = m * 2 = 2 m.
- It follows that the length of the segment is the hypotenuse sqrt( 2^2 + (
2m)^2).
- This expression is easily simplified to the form 2 sqrt(1 + m^2).
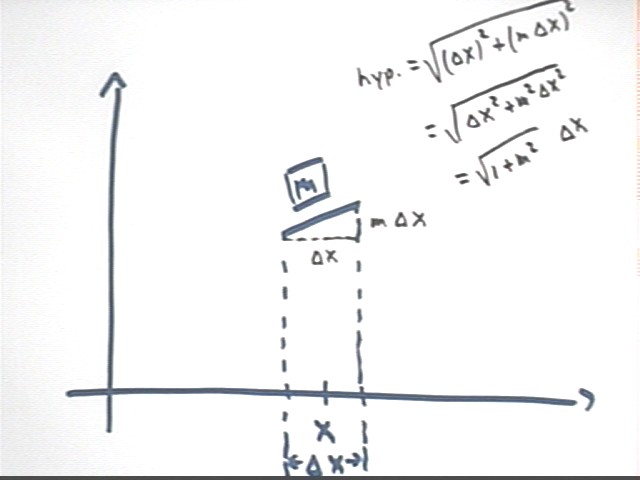
Find the length of a 'slope segment' corresponding to slope m on a
trapezoid of width `dx.
We again find the rise and the run of the 'slope segment', which is shown
below.
- The run is the width dx of the trapezoid.
- The rise is `dy = m * `dx,
- It follows that the length of the segment is the hypotenuse sqrt( 2^2 + (
m `dx)^2).
- This expression is easily simplified to the form sqrt(1 + m^2) * `dx
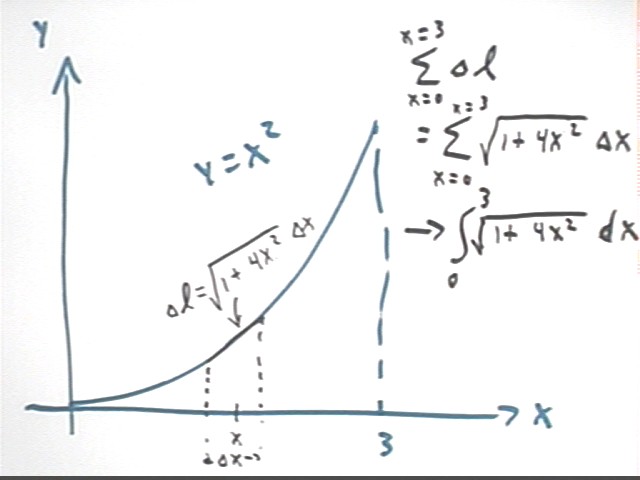
Find the length of a 'slope segment' corresponding a trapezoidal
approximation of width `dx, located in the vicinity of coordinate x, for the
function y = x^2.
We again wish find the rise and the run of the 'slope segment', which is
shown below.
- The run is the width `dx of the trapezoid.
- The slope is close to the slope at position x. If y = x^2 then this
slope is y ' = 2 x.
- The rise is `dy = slope * `dx = 2x * `dx
- It follows that the length of the segment is the hypotenuse sqrt( `dx^2 +
( 2x * `dx)^2).
- This expression is easily simplified to the form sqrt(1 + 4 x^2) * `dx.

Can we use these ideas to obtain an accurate expression for the arc length
of the y = x^2 curve between x = 0 and x = 3?
If we consider a typical small interval `dx containing coordinate x, we find
from the preceding analysis that the arc distance is very close to `dL = sqrt(1
+ 4x^2) * `dx.
Summing for a set of intervals which covers the interval from x = 0 to x = 3
we obtain sum ( sqrt(1+4x^2) `dx), from x = 0 to 3.
In the limit as `dx -> 0 on all intervals, the approximations
`dL = sqrt(1 + 4x^2) * `dx become more and more accurate, and the sum of all
the approximations approaches the accurate arc length.
The limiting value of the sum is the integral indicated below.
It is possible to integrate sqrt(1 + 4x^2) with respect to x, from x = 0 to x
= 3, using first a standard trigonometric substitution.
- We first substitute x = 1/2 tan(theta), as indicated below.
- We end up having to integrate 1 / cos^3(theta).
- This integral is not at all simple. We get antiderivative LN(TAN((2
theta + pi)/4))/2 + SIN(theta)/(2 COS^2(theta)); substituting theta =
arctan(2 x) we get LN(sqrt(4x^2 + 1) + 2x)/4 + x sqrt(4·x^2 + 1)/2
- Evaluating the antiderivative at the endpoints and subtracting we find
that the arc length is 9.747.
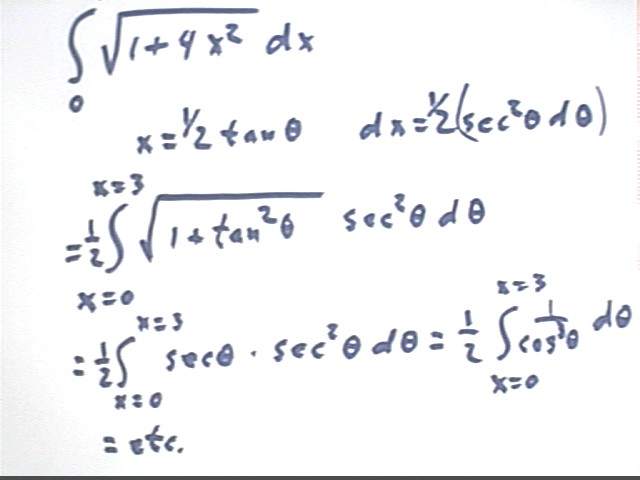
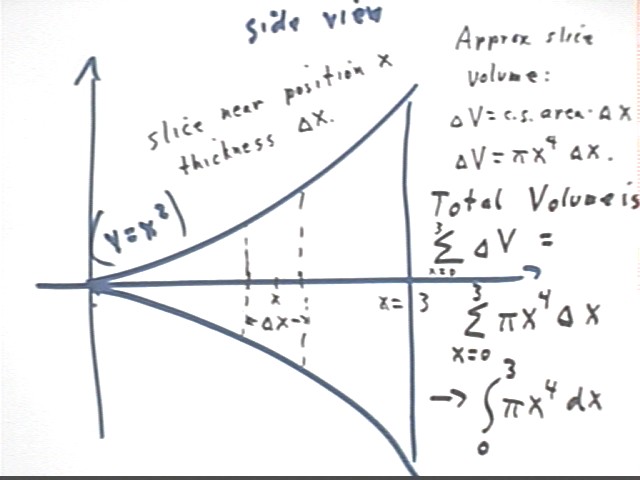
Find the volume of the solid of revolution formed by revolving y = x^2
about the x axis.
The solid is depicted in the figure below.
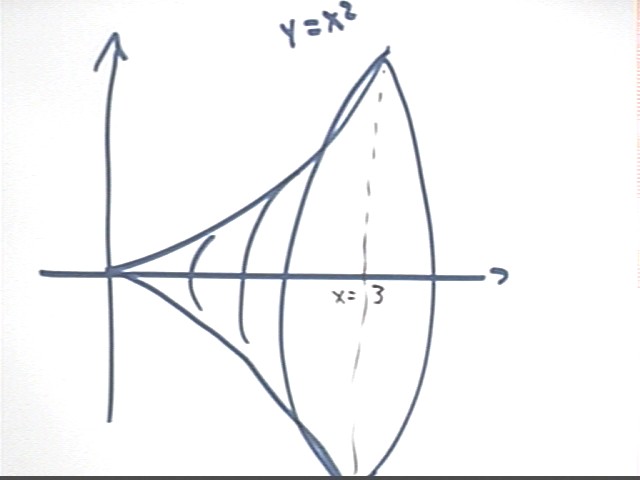
A side view of the solid shows a typical interval near coordinate x with
width `dx.
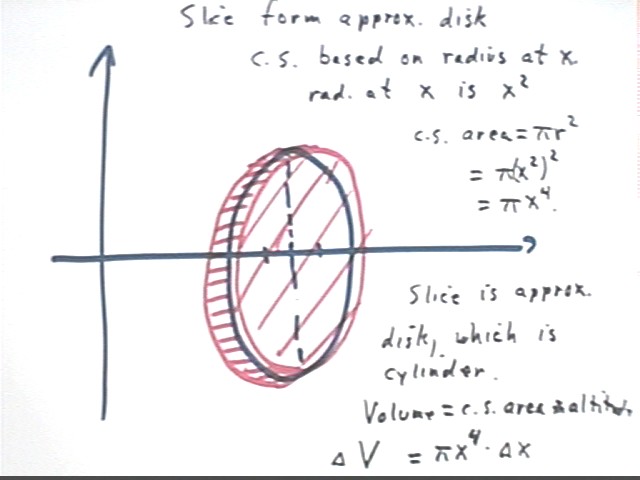
- This interval will correspond to a slice of the solid. A typical
slice is shown in the second figure below.
- If `dx is small then the average cross-sectional area of the slice must be
nearly equal to the cross-sectional area of a cut made at x.
- The radius of a cross-section at x is the distance from the x axis to the
curve y = x^2; the radius is therefore x^2.
- The c.s. area of a cut made at x is therefore pi r^2 = pi (x^2)^2 = pi
x^4, as shown in the second figure below.
- The thickness of the slice is `dx so the volume of the slice is
`dV = c.s. area * thickness = pi x^4 `dx.
- Summing such volumes from x = 0 to x = 4 and taking the limit as `dx ->
0 results, as shown below, in the integral
volume = int( pi x^4, x, 0, 3).
This integral is easily calculated. The antiderivative will be pi x^5 /
3. Between x = 0 and x = 3 this antiderivative changes by pi * 3^5 / 3 -
pi * 0^5 / 3 = 81 pi.
The volume of this solid is therefore 81 pi.