Calculus II Class 03/03

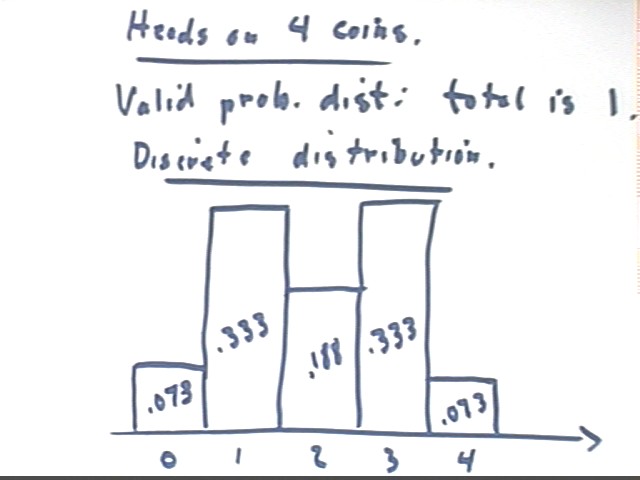
On 27 trials, flipping 4 coins on each trial and counting the number of Heads, tallies were 2, 9, 5, 9, 2 occurrences of 0, 1, 2, 3, 4 heads.  Using these numbers we obtain the distribution depicted below for the proportional # of Heads on 4 coins.

We think of x as the number of Heads and y as the proportion of all occurrences which show this number.

• For example the 'bar' corresponding to x = 1 has altitude .333, corresponding to the proportion 9/27 = .333 representing the number of occurrences of x = 1 as a proportion of the 27 outcomes.

Note that each bar of the histogram has width 1 so that the altitudes match the areas.

• The total of all these areas is 1.  Since the total of all the proportions must be 27/27 = 1, this is as it should be. 

The distribution of number of  'heads' is a discrete distribution, since only certain discrete values (in this case 0, 1, 2, 3, 4) are possible for the variable x = number of heads.

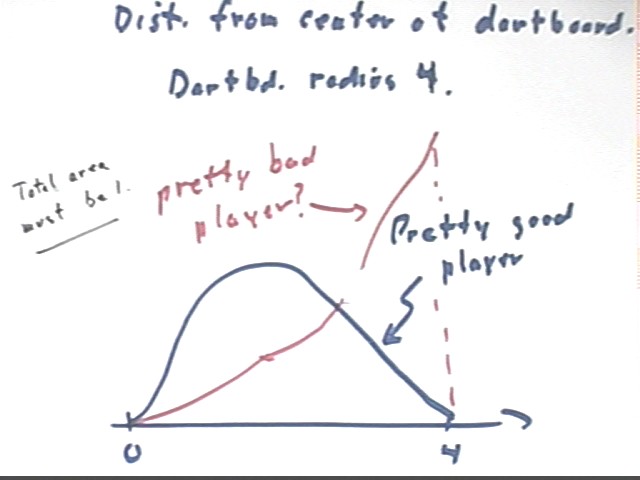
Consider a somewhat different situation.  What would the distribution of the distances x of 'hits' from the center of a dartboard look like?

• For a poor player the proportional number of 'hits' will go up as we move further from the center of the board.  This is because there is more area to hit between, say, 3 and 4 inches from the center than between 0 and 1 inches from the center (that outer ring has a lot more area than the bullseye).  A poor player will tend to hit the board at random, so that the number of hits near a given distance will be pretty much proportional to how much area is available at that distance.
• For a good player we expect that the 'hits' will be concentrated more toward the center.  The fact that there is very little area very close to the center means that there still won't be many hits at the very close distances, but despite the greater available area a good player won't hit the outer rings very often either.

We wish to make these ideas more precise.

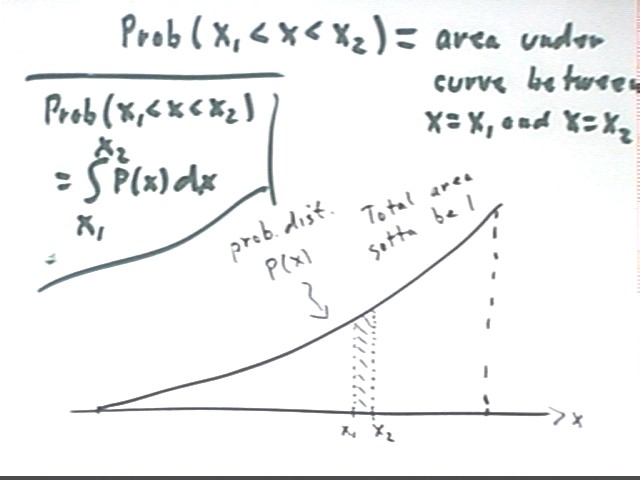
Let x be the distance a dart hits from the center of the dartboard.  Suppose that the probability of hitting between distances x1 and x2 from the center of a dartboard is equal to the proportional area of the dartboard lying between x1 and x2.  

If the radius of the dartboard is 4 then what is the probability Prob(x1 < x < x2)?

We sketch a hypothetical curve representing this situation.  If p(x) is the probability distribution function then the area beneath the p(x) curve between 0 and 4 must be 1 (since we're only counting what happens when the dartboard is hit, the probability of hitting somewhere between 0 and 4 must be 1).

The probability of hitting between distances x1 and x2 from the center is represented by the area under the curve between x = x1 and x = x2.

It should be clear that this area is the integral of the probability function p(x) from x = x1 to x = x2.

We will next use the geometry of the circle to find the formula for the function p(x). 

The total area between x = x1 and x = x2 is easily shown to be pi x2^2 - pi x1^2, and the total area of the circle is pi r^2 = pi * 4^2 = 16 pi.

• It follows that Pb(x1 < x < x2) is (x2^2 - x1^2) / 16 (see details below).
• Since Pb(x1<x<x2) is equal to the integral from x1 to x2 of the probability function p(x), we see that the integral of p(x) between these limits is x^2 / 16 - x1^2 / 16. 
• It should be clear from the Fundamental Theorem of Calculus that an antiderivative of p(x) is therefore x^2 / 16.  So p(x) is the derivative of x^2 / 16, or p(x) = x/8.

We can obtain this probability function by assuming a uniform distribution of 'hits'.  A uniform distribution is indicated in the figure below.  We will see in the next figure how we can use the uniformity of the distribution to construct the function p(x) = x/8.

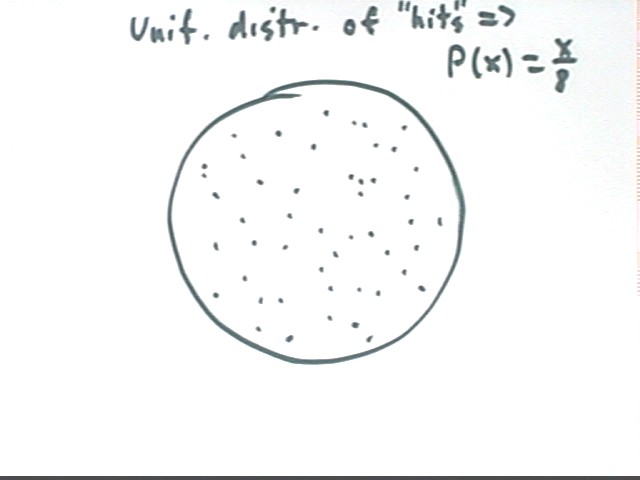
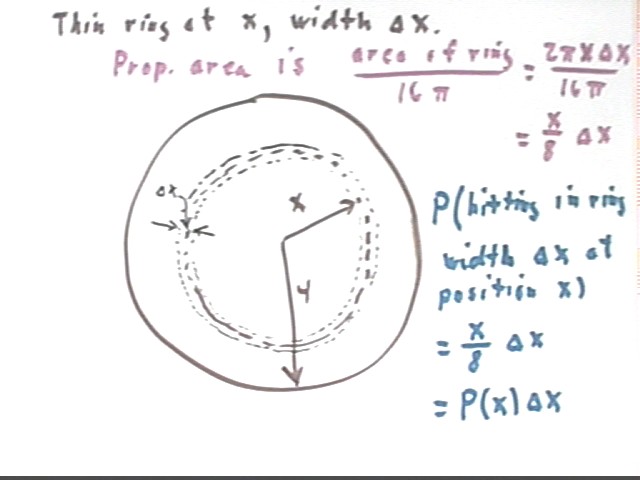
If we consider a thin ring at positoin x, having width `dx, we see that its area is approximately equal to 2 pi x `dx and that its proportional area is therefore x / 8 * `dx.

• Since the thickness of the ring is small, the area of the ring is equal to the product of its aveage circumference and its thickness.  Since average circumference is close to 2 pi x the area is 2 pi x `dx.
• We divide this area by the total area 16 pi to get proportional area 2 pi x `dx / (16 pi) = x/8 * `dx.
• Since the distribution of 'hits' is assumed to be uniform (a bad player, or even a good player at a great distance) the proportion x / 8 * `dx applies also to the probability.

Since the probability of a hit within a small range `dx of distance x is equal to the corresponding area beneath the p(x) vs. x curve, and since for small `dx this area is close to p(x) `dx, we see that at `dx -> 0 the two quantities p(x) `dx and x/8 `dx must approach one another, so that p(x) = x/8.

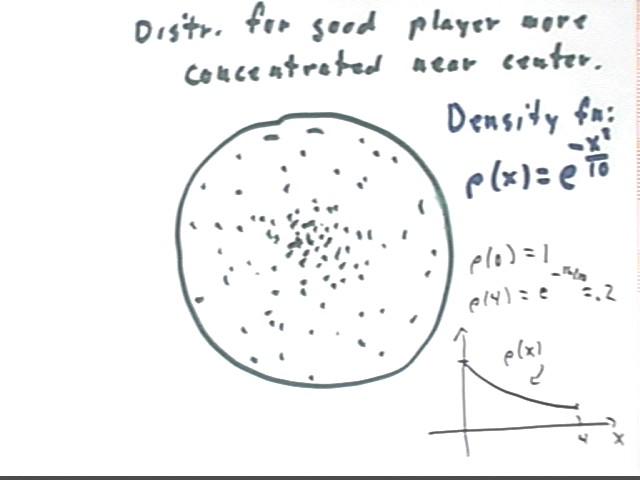
Now if we have a good player, statistical analysis will show us that the density of 'hits' over the area of the dartboard should be normally distributed, with density proportional to e^(.5 x / std dev)^2.

For the present example suppose that the density function for a certain player is rho(x) = e^(-x^2 / 10).   Note that this gives rho(0) = 1 and rho(4) = .2, approx..  So the density of 'hits' near the center is about 5 times the density near the outer rim.

The density function is a decreasing exponential, as depicted in the graph at lower right below.

The number of 'hits' in a region is equal to the average density of the region multiplied by the area of the region.

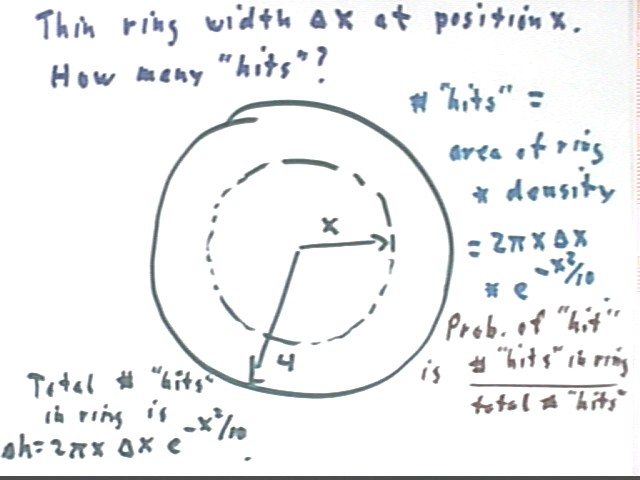
We again consider a thin ring of width `dx at position x.

• The number of 'hits' in this ring will be the product of the area of the ring and the density.
• The area is as before approximately `dA = 2 pi x `dx.
• For the present density function rho(x) = e^-(x^2/10) we therefore have

number of hits `dh = `dA * rho(x) = 2 pi x `dx * e^(-x^2/10).

The probability of a 'hit' in a certain region is the number of hits expected in that region, divided by the total number of 'hits'.

• The approximate total number of 'hits' is found by summing the number `dh = 2 pi x `dx * e^(-x^2/10) for all rings, from the center at x = 0 to the outer rim at x = 4.
• As `dx -> 0 this sum approaches the integral of 2 pi x * e^(-x^2/10), from x = 0 to x = 4.

The resulting integral is shown below, as is the probability of a 'hit' within the given ring.

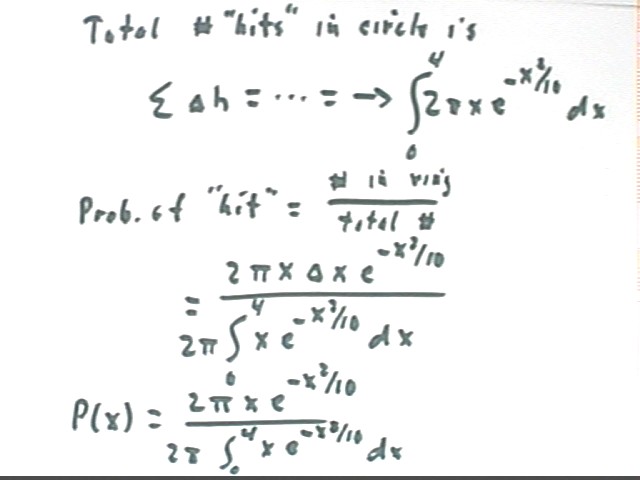
We note that the integral of p(x), from x = 0 to x = 4, must be 1.  You can easily check to see that this is so.

We can simplify the expression for p(x) by dividing 2 pi by 2 pi to obtain

• p(x) = x e^-(x^2/10) / int(x e^-x^2/10), x, 0, 4)

We can perform the integration in the denominator, using substitution u = -x^2/10 so that du = -x/5 dx and x dx = -5 du. 

• The integrand becomes -5 e^u with antiderivative -5 e^u = -5 e^(-x^2/10).
• Evaluating at the limits of the integral we obtain F(4) - F(0) = -1.009482589 - (-5) = 3.99.

Our function becomes p(x) = x e^-(x^2/10) / 3.99 or approximately p(x) = .25 x e^(-x^2/10).

This function has its peak slightly past x = 2.  This function is graphed below on the same graph as the uniform-density function p(x) = x / 8.

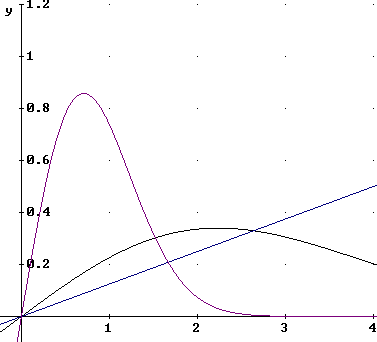
For a very good player the distribution function might be just rho(x) = e^(-x^2).

• You should verify that for this function the density near x = 4 is practically zero and that the x = 0 density is almost 3 times the x = 1 density.

The p(x) graph for this player is also depicted above, with the peak probability occurring for x less than 1.  The function for this player is 2.000000225·x·ê^(- x^2); you should be able to verify this result.

You should visually convince yourself that the area under each graph in the figure above is indeed plausibly close to 1.

You should also use derivative tests to verify that the function p(x) = .25 e^(-x^2/10) is indeed maximized for a value of x slightly greater than x = 2.

Challenge problem:  If the density of 'hits' is normally distributed with rho(x) = e^-(x^2 / c) for some c, then for what value of c will the density at x = 4 be just 1% of the x = 0 density?  What then will be the probability density function for 'hits'?