Calculus II Class 03/12

A geometric series has the form 

• sum(a * x^i, i from 0 to infinity) = a x^0 + a x^1 + a x^2 + ....  

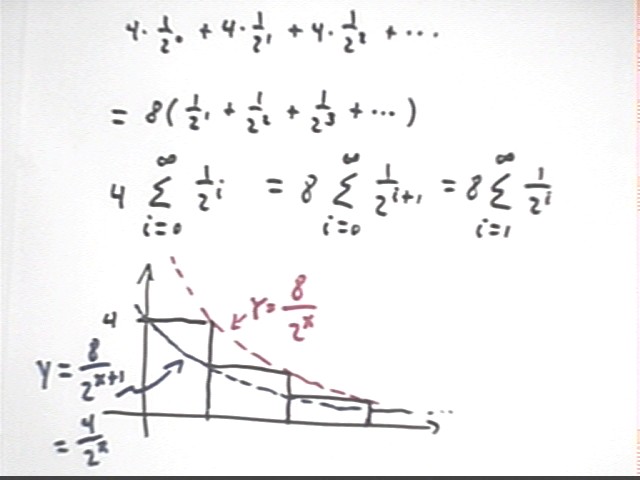
This sum is written out in the figure below in the form a x^0 + a x^1 + a x^2 + .... 

• An example of a geometric series we have already seen is provided by the series where a = 4 and x = 1/2.  

We note that 4 + 2 + 1 + 1/2 + ... can be written in two forms

• 4 + 2 + 1 + 1/2 + ... = 4 * 1/2^0 + 4 * 1/2^1 + 4 * 1/2^2 + ... = 4 * ( 1/2^0 + 1/2^1 + 1/2^2 + ... ) 

and

• 4 + 2 + 1 + 1/2 + ... = 8 * 1/2^1 + 8 * 1/2^2 + 8 * 1/2^3 + ... = 8 * ( 1/2^1 + 1/2^2 + 1/2^3 + ...  )

The first form can be written sum(4 * 1/2^i, i from 0 to infinity) while the second can be written as sum(8 * 1/2^i, i from 1 to infinity), the only difference being that for the second seriesi starts at 1.  Be sure you see that in both cases the starting value of i gives you 4 so that in both cases the series is 4 + 2 + 1 + 1/2 + ... .

It is also possible to write this series using 8 and allowing i to run from 0 to infinity.  This form is sum(8 * 1 / 2^(i+1), i from 0 to infinity).

The graph in the figure below shows the rectangles whose total area represent the sum of the series, along with the function y = 8 / 2^x lying 'above' these rectangles and the function y = 8 / 2^(x+1) lying 'below'.  We note that 8 / 2^(x+1) = 4 / 2^x; the connection between each of these functions and the corresponding way of expressing the sequence should be understood.

A typical series is expressed as a sum from i = 1 to infinity.  The form given for a geometric series is often in the form of a sum from i = 0 to infinity.  This can cause confusion if we don't know how to 'shift' the indices.  Remember that:

• A geometric series can be expressed as sum( a x^i, i from 0 to infinity).
• The same series can be expressed as sum( a x^(i-1), i from 1 to infinity).
• The first term of either series is a * x^0 = a.  Be sure you understand why.

The Nth partial sum S(N) of a series is the sum of its first N terms.

• If the series is sum(a(i), i from 1 to infinity) then it can be written as a1 + a2 + a3 + ...
• The sum of the first N terms is S(N) = a1 + a2 + a3 + ... + aN.
• This is expressed in summation notation as sum(a(i), i from 1 to N), written as indicated in the figure below.

For the series 4 + 2 + 1 + 1/2 + ... defined by a(i) = 8 / (2^i), i from 1 to infinity, we get the following partial sums:

• the third partial sum S(3) = 4 + 2 + 1 = 7, the sum of the first three terms

and

• the fifth partial sum S(5) = 4 + 2 + 1 + 1/2 + 1/4 = 7  3/4, the sum of the first five terms.

From what we have already seen about this series we know that as N gets larger and larger the partial sums behave as follows:

• S(N) gets closer and closer to 8 as N increases
• S(N) in fact lies within 1 / 2^N of 8, so that
• since 1 / 2^N can be made as small as we wish by choosing sufficiently large N, it follows that S(N) can be made as close to 8 as we wish.

Our conclusion is that S(N) approaches 8 as a limit.  

We express this by saying that

• sum(8 / 2^i, for i from 1 to infinity) = limit{N -> infinity}(S(N)) = 8.

In general if the partial sums S(N) of a given series approach a limit as N -> infinity, the series is said to converge, whereas if S(N) does not approach a limit the series is said to diverge.

The series sum(a x^n, n from 0 to infinity) = a + a x + a x^2 + ... can be factored to give the form a ( 1 + x + x^2 + ... )

• sum(a x^n, n from 0 to infinity) = a + a x + a x^2 + ... =  a ( 1 + x + x^2 + ... ):

It can be proven that the partial sums S(N) = 1 + x + x^2 + ... + x^(N-1) of the series 1 + x + x^2 + x^3 + ... is 

• for geometric series:  S(N) = 1 + x + x^2 + ... + x^(N-1) = (1 - x^N) / (1-x) for x not equal to 1.

Since x^N approaches zero for large N whenever | x | < 1 and diverges when | x | > 1 it follows that (1 - x^N) / (1-x) converges for | x | < 1 and diverges for | x | > 1.  Thus the sequence of partial sums S(N) converges for any x such that | x | < 1 to 1 / (1-x) and we say that

• sum(a x^n, n from 0 to infinity) = a ( 1 + x + x^2 + ... ) = a * 1 / (1 - x) = a / (1 - x).

Applying this formula to the geometric series 4 + 2 + 1 + 1/2 + ... we conclude that the series converges to 8:

For the series 4 + 2 + 1 + 1/2 + ... the partial sums are 4, 6, 7, 7 1/2, 7 3/4, ... .

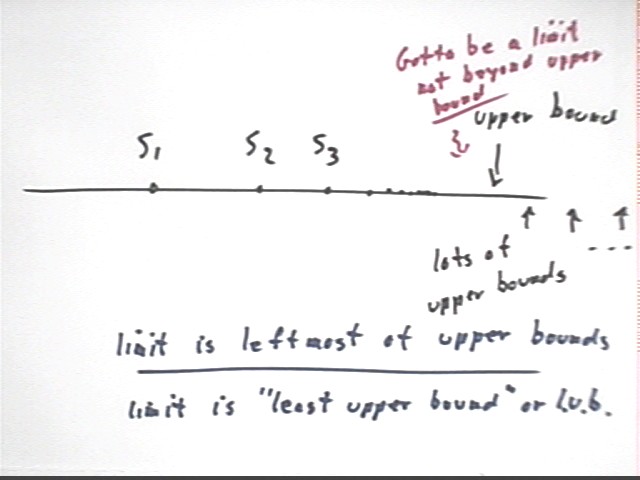
An upper bound of the partial sums is any number which greater than any of the partial sums.  

For example, knowing that the partial sums S(N) of the above series 4 + 2 + 1 + 1/2 + ...  never exceed 8 we can say that any number greater than 8 is an upper bound for the partial sums.  

• For example, 10 is greater than any of the partial sums so 10 is an upper bound for the partial sums. 
• For that matter, 1000 is an upper bound.

If a sequence of upper bounds has a finite upper bound then there are infinitely many upper bounds, since any number greater than the finite upper bound is also an upper bound.  

We aren't really interested in how many upper bounds there are, and we aren't really interested in any of the upper bounds except one.  

• The upper bound we are really interested in for the given series 4 + 2 + 1 + 1/2 + ... is 8, which is the limiting value of the sequence of partial sums and hence the sum of the series.
• Of all the upper bounds of the sequence of partial sums, 8 is the smallest.  No number less than 8 can be an upper bound, since for any number S less than 8 is is possible to find an N such that S(N) exceeds x (if S < 8 then just choose N such that 1 / 2^N is less that 8 - S; S(N) will be greater than S). 

With this discussion in mind, imagine that a series has partial sums S1, S2, S3, ... with the property that each partial sum is greater than the one before it.  Then the partial sums will look something like those indicated on the number line below. 

Suppose that we know that there is some upper bound for this sequence.  From what we've seen it follows that there are many upper bounds for the sequence.  We observe the following:

• Of all the upper bounds there is one specific number that is the smallest.
• This smallest upper bound is the limit of the sequence of partial sums, and is therefore the sum of the series.

Recall that sum(8 / 2^i, i from 1 to infinity) converges to 8.

Since sum(36 / 3^i, i from 1 to infinity) can be written as 12 (1 + 1/3 + 1/3^2 + ... ) the series is geometric and must converge to 12 ( 1 / ( 1 - 1/3) ) = 18.

Another series is sum(8 / 2^i + 36 / 3^i, i from 1 to infinity).  It seems very plausible that this series, being the sum of series converging to 8 and to 18, will converge to 8 + 18.  It is not difficult to prove this by considering the partial sums of the 'new' series.

This is an instance of the theorem that tells us that if sum(a(i)) = a and sum(b(i)) = b, sum(a(i) + b(i) ) = a + b.

Other seemingly obvious properties of series can also be proved.

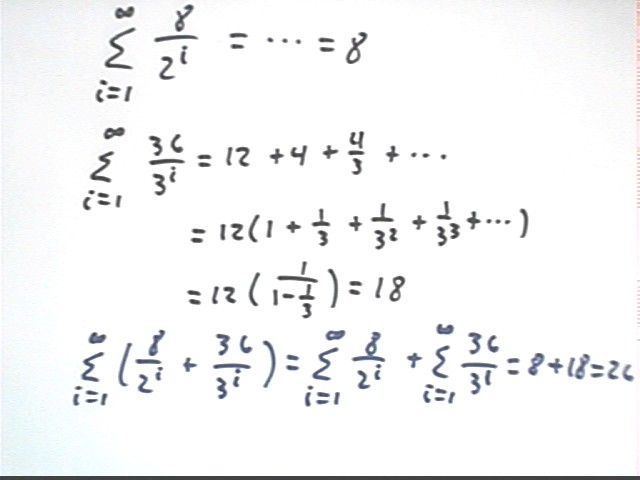
Now consider the question of whether sum(8 / ( i * 2*i), i from 1 to inifinity) converges:

• Writing out the first several terms of this series we note its resemblance to the series sum(8 / 2^i).
• A little consideration shows that 8 / (i * 2^i), with that i in the denominator, is never greater than 8 / 2^i. 
• We can prove this by rearranging the inequality 8 / (i * 2^i) <= 8 / 2^i.  Multiplying both sides by the positive number 2^i / 8 , in fact, gives us 1 / i <=1, or 1 <= i.  Since i is always at least 1, this is true and confirms algebraically that 8 / (i * 2^i) < 8 / 2^i.

Where does this get us?  Well, we know from what by now should be vast experience that sum(8 / 2^i) converges (to 8).  If the terms of another series are never greater than the terms of this series, then that series must also converge (and to a number not greater than 8). 

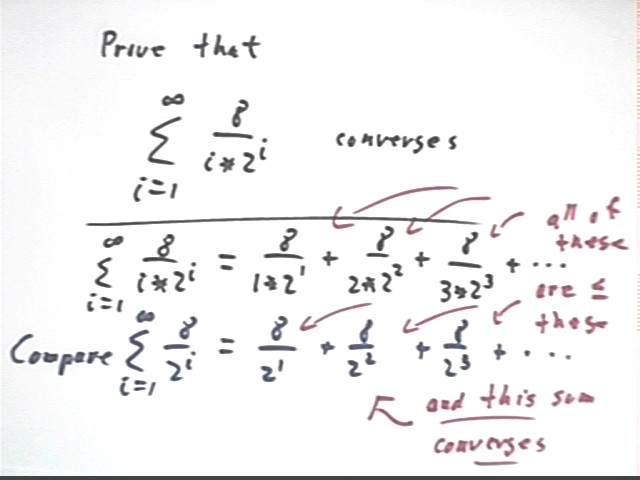
The figure below illustrates these two series as areas beneath two series of rectangles.

• The 8 / 2^i rectangles have total area 8.
• The 8 / (i * 2^i) rectangles clearly contain less area, so their total area is less than 8.

It follows that the 8 / (i * 2^i) series converges.

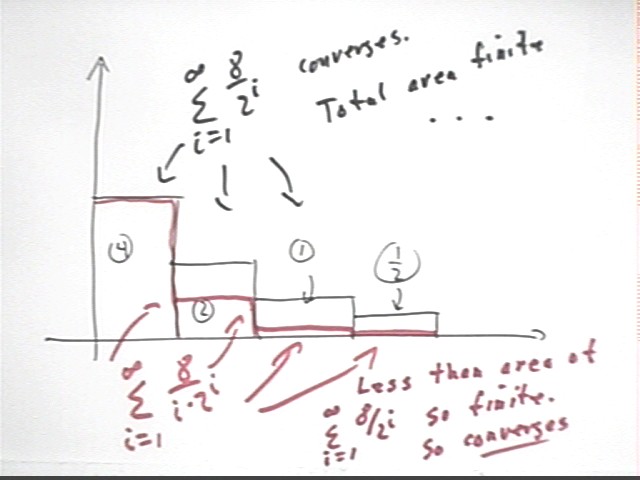
Now let's see if we can use similar reasoning on the series defined by 8 * i / 2^i.  We compare this series with the known convergent series defined by 8 / 2^i.

• Writing out the first few members of this sequence we see that 8 * i / 2^i is never less than 8 / 2^i, and usually greater.

This gives us the picture below, where the total area beneath the 8 * i / 2^i rectangles exceeds that beneath the 8 / 2^i rectangles.

We know that the total area under the 8 / 2^i rectangles is finite.  What can we conclude about the total area under the 8 * i / 2^i rectangles?

• We can conclude only that the total area under the 8 * i / 2^i rectangles is greater than a quantity we know to be finite.
• This total area could be a larger finite number.  Alternatively the total area might well be infinite.  From the fact that a quantity is greater than some finite quantity we cannot draw any firm conclusions. 

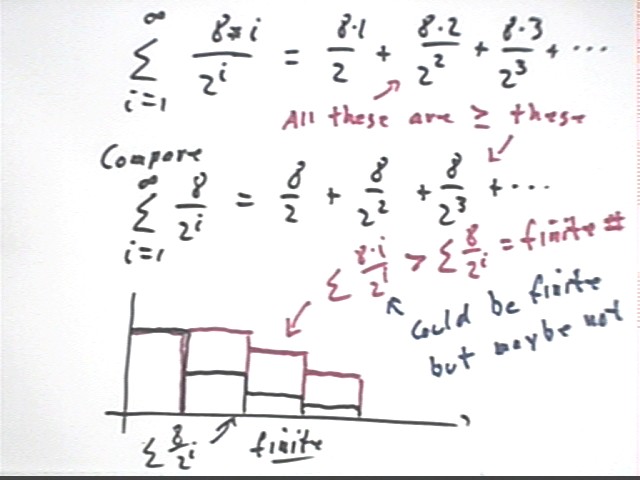
We can't prove it by making a comparison with the 8 / 2^i series but it turns out that the 8 * i / 2^i series does indeed converge.  We reason as follows:

• If | x | < 1 a geometric series converges.
• For the convergent geometric series the ratio of the n+1 term to the preceding term (the n th term) is 

ratio = (a x^n) / (a x^(n-1)).  

• Simplifying this we get ratio = x.  So if | x | < 1 the ratio of each term to its predecessor is always x with | x | < 1. 

We conclude that any sequence where the absolute value of the ratio of each term to its predecessor stays less than 1 should behave like a geometric sequence in that it converges.

A rigorous proof that it is so can be accomplished and the proof follows this line of reasoning.

We apply this reasoning to the series defined by 8 i / 2^i:

• The n+1 term of this series is a(n+1) = 
• 8 ( n + 1) / 2^(n+1).
• The n th term of this series is a(n) = 8 ( n ) / 2^(n).
• The ratio is therefore 

ratio = a(n+1) / a(n) = [ 8 ( n + 1) / 2^(n+1) ] / [ 8 ( n ) / 2^(n) ].

• This ratio is easily simplified (invert the denominator and multiply), then do the algebra as indicated below) to 

ratio = (1 + 1/n) / 2.

As n approaches infinity, 1/n approaches zero and the ratio approaches

• limiting value of ration as n -> infinity:  (1 + 0) / 2 = 1/2.

Since the ratio approaches 1/2 the series must eventually behave much like a geometric series with ratio 1/2.  The result must be a series with a finite sum because:

• Whatever happens up to the point where the series starts acting like a geometric series, the series up to that point contains only finitely many finite terms and so must be finite.
• The part that acts like a geometric series has to converge to a finite sum.
• The series can therefore be broken into two parts, both with a finite sum.  Since the total of two finite quantities is finite, the total sum must be finite.

In fact the argument just given isn't quite right.  We can't really say that the series must eventually behave much like a geometric series with ratio 1/2.  But we can say that for any number x greater than 1/2 (say, x = .50001) the series must converge faster than a geometric series with common ratio x.  The argument is easily adapted.