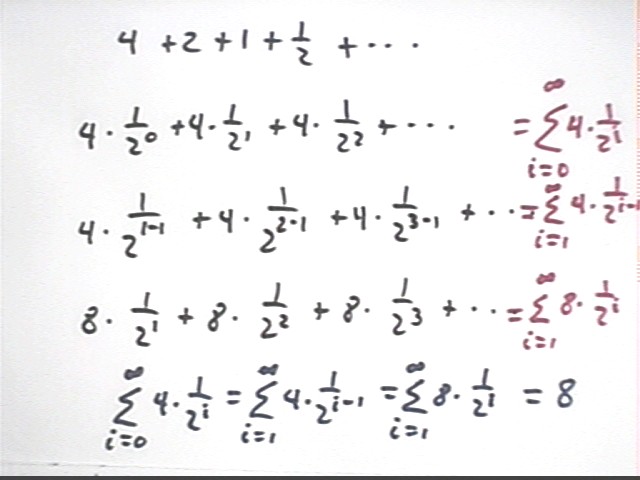
Calculus II Class 03/14

The series 4 + 2 + 1 + 1/2 + ... converges to 8, as we have seen.

This series can be factored as 4 ( 1 / 2^0 + 1 / 2^1 + 1 / 2^2 + ... ) and therefore written as

• 4 + 2 + 1 + 1/2 + ... = 4 * sum( 1 / 2^i, i from 0 to infinity).

Alternatively we can let i run from 1 to infinity and let the power of 1 / 2 be i - 1, so that the powers still run from 0 to infinity.  We can therefore write the sequence in a second form as

• 4 + 2 + 1 + 1/2 + ... = 4 * sum( 1 / 2^(i-1), i from 1 to infinity).

Finally we can write the series as 4 + 2 + 1 + 1/2 + ...  = 8 ( 1 / 2^1 + 1 / 2^2 + 1 / 2^3 + ... ) or

• 4 + 2 + 1 + 1/2 + ... = 8 * sum( 1 / 2^(i), i from 1 to infinity).

You should understand the how these three expressions for the series 4 + 2 + 1 + 1/2 + ... are related.

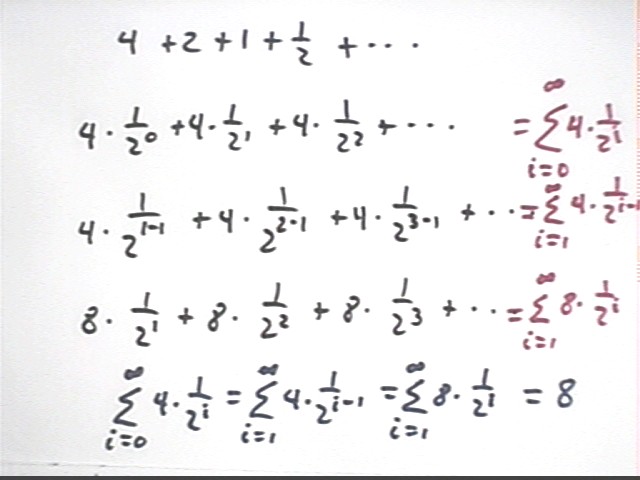
Now consider the sum 8 * 1 / 2^1 + 8 * 2 / 2^2 + 8 * 3 / 2^3 + ... .  We wish to determine whether this sequence converges or diverges.

• Each term of this sequence is greater than the corresponding term of the sequence 8 / 2^1 + 8 / 2^2 + 8 / 2^3 + ... = 4 + 2 + 1 + 1/2 + ... , which as we have seen converges to 8.
• Being greater term by term than a convergent sequence does not guarantee either convergence or divergence, as we have seen.
• So a direct comparison with at least the convergent sequence 8 / 2^1 + 8 / 2^2 + 8 / 2^3 + ... does not tell us anything.\

If the sequence somehow acts, at least beyond some point, like a geometric sequence then we can guarantee its convergence.

• The characteristic of a convergent geometric sequence is that each term is less than the one before it by a certain fixed ratio a(n+1) / a(n) = r, with | r < 1..
• So it makes sense to look at the ratios a(n+1) / a(n) of the present sequence.

For the present series, a(n+1) = 8 ( n+1) / 2^(n+1), and a(n) = 8 n / 2^n.

• The ratio us a(n+1) / a(n) = 8 ( n+1) / 2^(n+1) / [ 8 n / 2^n ] = (n+1) / n * 2^n / 2^(n+1) = (1 + 1/n) / 2.
• For any n greater than 1 this ratio is less than (1 + 1/2 ) / 2 = 3/4 < 1.   So for any n > 1 the remaining series converges faster than a geometric series.
• For example if n > 10 we can say that the remaining series, starting with n = 11, converges faster than a geometric series with ratio (1 + 1/10) / 2 = .55.

In general as long as the limit of | a(n+1)  / a(n) | is less than 1, the series must converge.

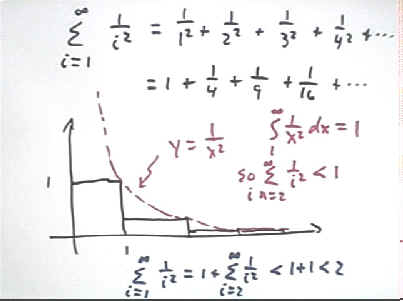
The series 1/1^2 + 1/2^2 + 1/3^2 + ... = sum(1 / i^2, i from 1 to infinity) can be shown to converge if we compare it to the integral from 1 to infinity of 1 / x^2.

• As shown in the figure below the rectangles representing all but the first member of the series all lie beneath the y = 1 / x^2 curve, from x = 1 to infinity.
• The total area in the rectangles represents the total of the series, and is clearly less than the total area under the curve.
• Since we easily integrate 1 / x^2 for x from 1 to infinity, obtaining result 1, the series from i = 2 to infinity must converge to a number less than 1.
• Since the first member of the series is 1, the entire series from i = 1 to infinity must converge to a number less than 2.

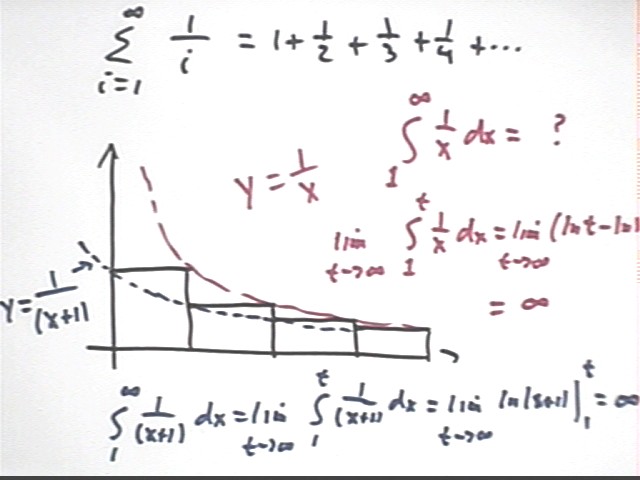
On the contrary the series 1 + 1/2 + 1/3 + 1/4 + ... can be shown to diverge:

• We first try the same strategy we used above, placing the rectangles representing the series underneath the curve y = 1 / x.
• Integrating 1 / x from 1 to infinity, however, tells us that the integral diverges toward infinity.
• Our series has less area than that under the curve, and might therefore be finite or infinite.
• Suspecting that the series might be divergent, we shift the graph of y = 1 / x one unit to the left, obtaining the indicated curve for y = 1 / (x + 1).
• The rectangles representing the series lie above this curve.  Integrating we find that the area under the curve diverges to infinity, indicating that the series also diverges toward infinity.

Consider the function 1 / x^1.01.  Its antiderivative is -100 / x^.01.   Because there is a positive power in the denominator, this antiderivative approaches zero as x -> infinity and the  integral of 1 / x^1.01 from 1 to infinity converges.

• The same happens for 1 / x^1.001, or 1 / x^1.0001, or in general for 1 / x^p whenever p > 1.

We already saw above that the corresponding integral of 1 / x^1, with antiderivative ln x, diverges.

For if p > 1 the integral converges, if p = 1 the integral diverges.   What happens if p < 1?

For example if p = .999 our function is 1 / x^.999 and its antiderivative is 1000 x^.001.  This antiderivative, with a positive power of x now in the numerator, approaches infinity as x -> infinity, causing the integral of 1 / x^.999 to diverge on the interval [1, infinity).

• The same happens for 1 / x^.9999, or 1 / x^.99999, or for that matter for 1 / x^.1 or 1 / x^.01.

We therefore conjecture that

• For if p > 1 the integral of 1 / x^p, from x = 1 to infinity, converges, while if p = 1 or p < 1 the integral diverges.

We can establish this result in more general terms:

Since an antiderivative of 1 / x^p is - 1 / [ (p-1) x^(p-1)], which when p > 1 is a negative power of x and when p < 1 is a positive power of x, we conclude that the integral from x = 1 to infinity of 1 / x^p converges for p > 1 and diverges for p < 1.  We have already seen that when p = 1 the integral diverges.

It follows by the comparisons we have already seen that the sum from i = 1 to infinity of 1 / i^p converges for p > 1 and diverges for p < 1.

This result is quoted in the top half of the figure below.

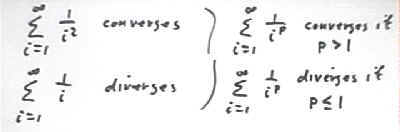
This result is quoted in the top half of the figure below.

In the figure below we attempt a ratio test on the series sum(1 / i^2, i from 1 to infinity).  Recall that we just showed this series to be convergent.

• For this series a(n) = 1 / n^2 and a(n+1) = 1 / (n+1)^2.
• It follows that lim{n -> infinity}(a(n+1) / a(n) ) = lim{n ->infinity}(1 / (1 + 1/n))^2  = 1.

We know that for some series a ratio limit of 1 indicates divergence (e.g., for the seris 1 + 1 + 1 + 1 + ... the limiting ratio is 1 but the series clearly diverges).   However here we have an example of a convergent series for which the limit of the ratio is 1.

This shows that a series with limiting ratio 1 can converge or diverge, and that limiting ratio 1 therefore tells us nothing one way or the other about convergence.

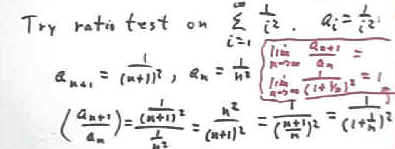
As shown below a ratio test on the series sum(1 / i, i from 1 to infinity), shown before to be divergent, gives us limiting ratio 1.

This example further illustrates that limiting ratio 1 is inconclusive regarding the convergence of a series.

We apply our knowledge that the series defined by 1 / i^2 converges to show that the series defined by 1 / [ i^2 ( 2 + cos(i) ] must also converge.

We first note that this new sequence has 1 / i^2 as a factor, also containing 2 + cos(i) as a factor of its denominator.

We consider this factor 2 + cos(i).  How big or how small can it be?

• Since the value of the cosine function ranges from -1 to 1, we see that cos(i) ranges from -1 to 1.
• Since -1 < cos(i) < 1 it follows that -1 + 2 < 2 + cos(i) < 1 + 2, so that 1 < 2 + cos(i) < 3.
• From this it follows that 1 / (i^2 (2 + cos(i) ) lies between 1 / (3 i^2) and 1 / (1 i^2).

Now since the sequence defined by 1 / i^2 converges, and since every term of 1 / (i^2 ( 2 + cos(i) ) of the new sequence has been shown to be less than the corresponding term 1 / i^2 of the convergent sequence, it follows that the new sequence is also convergent.