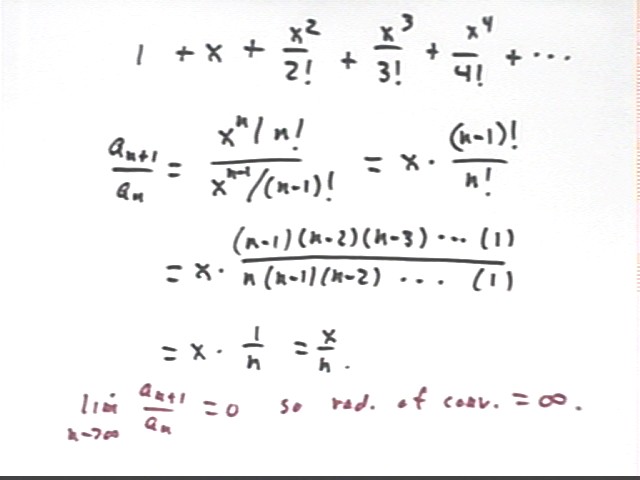Calculus II Class 03/24
Does the sequence 1 + x + x^2 + x^3 + ... converge?
This is a geometric series with common ratio r = x. If | x | < 1, as we have seen, this sequence converges to 1 / (1-x).
| x | < 1 means that x < 1 and -1 < x, or -1 < x < 1. This interval is depicted below and the interval of convergence.
Note that this interval is centered at x = 0 and extends 1 unit in either direction. We say that the interval is centered at x = 0 and has radius of convergence 1.
We therefore say that the sequence 1 + x + x^2 + ... converges about x = 0, with radius of convergence 1.

Does the sequence 1 + 2x + (2x)^2 + (2x)^3 + ... converge?
This sequence is of the form 1 + r + r^2 + r^3 + ... for r = 2x. This makes it a geometric series.
A geometric series converges if | r | < 1.
Since r = 2x, the series converges if | 2x | < 1.
We therefore see that the series converges if | 2x | < 1, i.e., if | x | < 1/2.
| x | < 1/2 means -1/2 < x < 1/2, and interval centered at x = 0 and extending 1/2 unit in both directions.
We say that this series converges about x = 0 with radius of convergence 1/2.

The series 8 + 8 (x/4) + 8 (x/4)^2 + 8 (x/4)^3 + ... can be factored into the form 8 ( x/4 + (x/4)^2 + (x/4)^3 + ... ).
The second factor is a geometric sequence with r = x/4.
This sequence therefore converges for | x/4 | < 1, or -4 < x<? 4.
The sequence converges about x = 0, with radius of convergence 4.
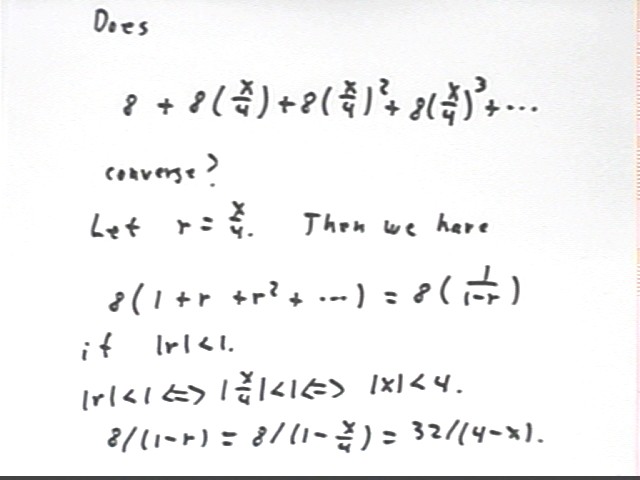
The series 1 + (x-3) + (x-3)^2 + (x-3)^3 + ... is a geometric series with r = x-3.
This sequence converges for | x-3 | < 1.
| x-3 | < 1 means -1 < x-3 < 1, or 2 < x < 4.
This interval |x-3| < 1 is centered at x = 3, and extends 1 unit in either direction from x = 3.
We say that this series converges about x = 3, with radius of convergence 1.

The sequence shown below converges for | 2 x - 8 | < 1, which simplifies to | x - 4 | < 1/2.
This interval is centered at x = 4 and extends 1/2 unit in either direction from x = 4.
The interval of convergence is centered at x = 4 and the radius of convergence is 1/2.

Does the sequence 1 + x + x^2 / 2 + x^3 / 3 + x^4 / 4 + ... converge, and if so can we find the interval of convergence?
We note that this series is not geometric. The ratio a(n+1) / a(n) of a member of the sequence to its predecessor is not constant.
However the ratio a(n+1) / a(n) does approach a limit, which allows us to determine the radius of convergence.
a(n) = x^(n-1) / (n-1) and a(n+1) = x^n / n.
The ratio a(n+1) / a(n) is therefore x^(n-1) / (n-1) / [ x^n / n ] = x ( 1 - 1/n ), as shown below.
As n -> infinity this ratio approaches x.
We know that a series converges if the magnitude of its ratio is less than 1, so we conclude that
the series 1 + x + x^2 / 2 + x^3 / 3 + ... , whose ratio approaches limit x, therefore converges if | x | < 1.
Note that this is the same interval of convergence as for 1 + x + x^2 + x^3 + ... The number in the denominator of the present sequence does not affect the interval of convergence, though it will affect the value of the sum of the sequence.
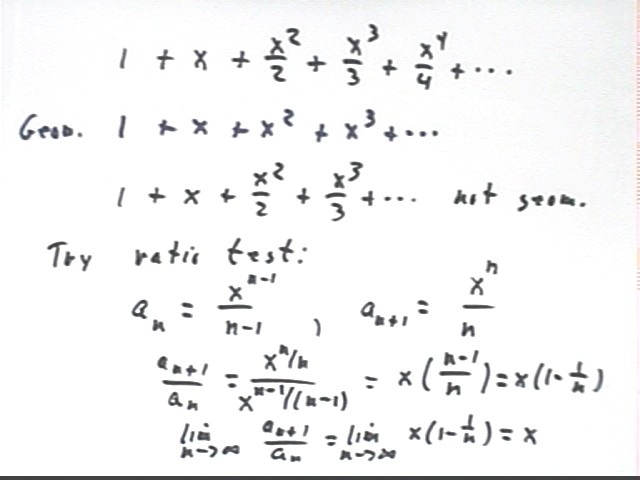

The same procedure can be applied to the sequence 1 + x + x^2 / 2^2 + x^3 / 3^3 + ...
We first note that the number in the denominator, and the power to which it is raised, are both equal to the power of x.
Thus the nth term of this sequence is x^(n-1) / (n-1)^(n-1).
As shown below the ratio a(n+1) / a(n) for this sequence is x / n * ((n-1) / n)^(n-1).
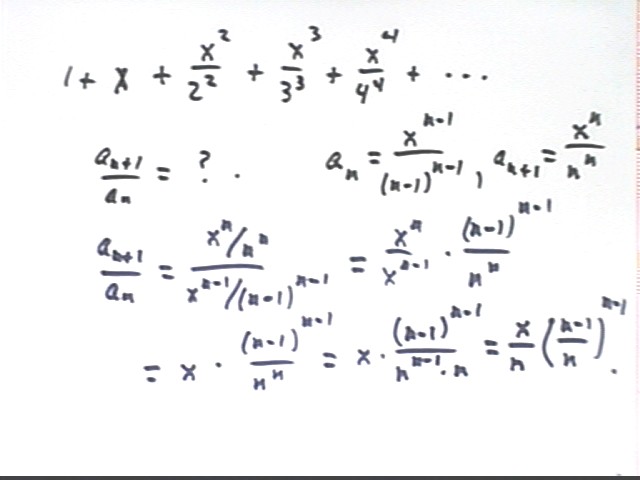
The limiting value of a(n+1) / a(n) = x / n * ((n-1) / n)^(n-1) can be found as follows:
For any x, as n -> infinity the value of x / n can be made as small as we like, and therefore approaches limit 0.
((n-1) / n) has a numerator which is smaller than its denominator and is therefore less than 1. It follows that ((n-1) / n)^(n-1) must also be less than 1 for any value of n.
Since for any x the ratio a(n+1) / a(n) = x / n * ((n-1) / n)^(n-1) is therefore the product of a factor that as n -> infinity approaches 0 and a factor that never exceeds 1, the limiting value of this ratio is zero.
This limit occurs for any value of x. Since the series converges when the magnitude of the ratio is < 1, we conclude that the series converges for any x.
We say that the radius of convergence of this sequence is inifinite.
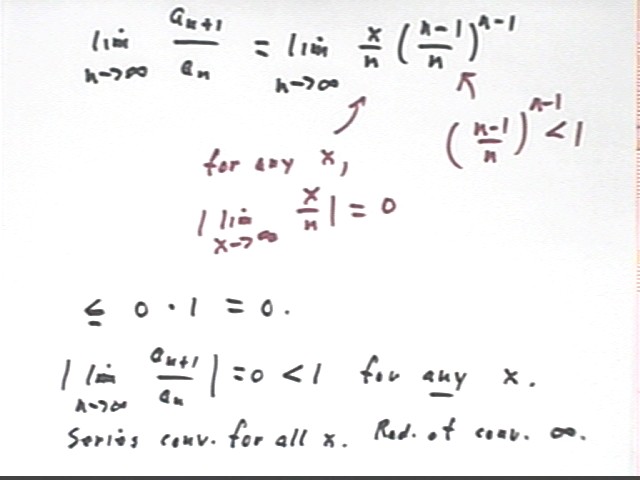
The sequence 1 + x + x^2 / 2! + x^3 / 3! + ... has ratio a(n+1) / a(n) = x / n! * (n-1)! , as shown below.
n ! is the product of all the integers from n down to 1. That is, n ! = n * (n-1) * (n-2) * (n-3) * ... * 3 * 2 * 1.
As shown below it follows that (n-1)! / n! = 1 / n, so that the limiting value of the ratio is 0.
As before, the radius of convergence is inifinite.