Calculus II Class 03/28

Recall the nth degree Taylor polynomial, obtained by matching at x = 0 the first n derivatives of f(x) with the first n derivatives of a degree-n polynomial:

Pn(x) = f(0) + f ' (0) * x + f '' (0) * x^2 / 2! 

+ f '''(0) * x^3 / 3!  + f ''''(0) * x^4 / 4! + ... + f[n] * x^n / n!

We saw that as n increases, Pn(x) 'works' for greater and greater intervals around x = 0.

If we extend this series so it goes forever, then if f is continuously differentiable to all degrees the result converges for every x inside the interval of convergence to f(x) and we say that

f(x) = f(0) + f ' (0) * x + f '' (0) * x^2 / 2! + f '''(0) * x^3 / 3!  + f ''''(0) * x^4 / 4! + ... + f[n] * x^n / n! + ... 

The Taylor polynomials Pn(x) were approximations.  This series is the real thing--it converges to f(x) for every x within the radius of convergence.

The Taylor series can be written down if we can find an expression for f[n](x), the nth derivative of f(x), for arbitrary n.

This usually involves looking at the pattern of successive derivatives.

We saw for example that the successive derivatives of y = sin(x) were

• y = sin(x)
• y ' = cos(x)
• y '' = - sin(x)
• y ''' = -cos(x)
• y '''' = sin(x)
• y ''''' = cos(x)
• y '''''' = - sin(x)
• y ''''''' = -cos(x)
• y '''''''' = sin(x)

The repeating pattern is clear.  We also easily see that at x = 0 the function and derivatives are 

• y = 0
• y ' = 1
• y '' = 0 
• y ''' = -1
• y '''' = 0
• y ''''' = 1

etc., repeating in the pattern 0, 1, 0, -1, 0, 1, 0, -1, 0, 1, ... .

Let's look at the pattern of derivatives for y = e^x.

We see very quickly that 

• y ' = e^x, y '' = e^x, y ''' = e^x, etc..  

At x = 0, 

• y = 1, y ' = 1, y '' = 1, etc..

So the Taylor Series f(x) = f(0) + f ' (0) * x + f '' (0) * x^2 / 2! + f '''(0) * x^3 / 3!  + f ''''(0) * x^4 / 4! + ... + f[n] * x^n / n! + ...  becomes

• f(x) = 1 + 1 * x + 1 * x^2 / 2! + 1 * x^3 / 3!  + 1 * x^4 / 4! + ... +1 * x^n / n! + ... 

or

• f(x) = 1 + x + x^2 / 2! + x^3 / 3!  + x^4 / 4! + ... +x^n / n! + ... 

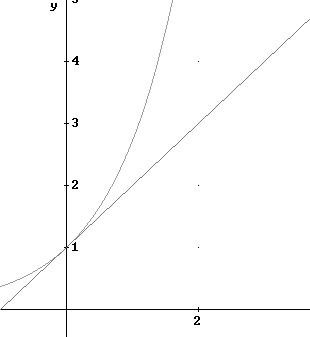
The figure below shows the graph of y = e^x along with the graph of the first two terms 1 + x of the expansion.

The next figure shows the preceding graphs in addition to the graph of the first three terms 1 + x + x^2 / 2! of the expansion.

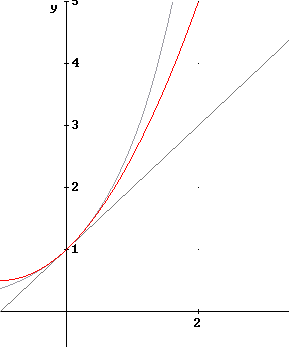
The next figure adds the graph of the first four terms 1 + x + x^2 / 2! + x^3 / 3!of the expansion.

This series of figures demonstrates the convergence of the Taylor series to the exponential function, at least over the range demonstrated here.

Now look at f(x) = ln(x).  We first consider the sequence of its successive derivatives:

• f(x) = ln(x)
• f ' (x) = 1 / x
• f ''(x) = -1 / x^2
• f '''(x) = 2 / x^3 = 2! / x^3
• f '''' (x) = -3 * 2 / x^4 = -3! / x^4
• f ''''' (x) = 4 * 3 * 2 / x^5 = 4! / x^5

The pattern of the derivatives is an alternating sign (+ then 1 then + then 1 etc.), with the factorial being of the number which is one less than the derivative (e.g., 2! for 3d derivative, 3! for 4th dreivative, etc.). 

We speculate that the nth derivative is something like

• f[n](x) = (-1)^n * (n-1)! / x^n  ???? 

But this doesn't quite work.  For n = 2 this gives us f ''(x) = (-1)^2 * (2-1)! / x^2 = 1 / x^2, not -1 / x^2.  This formula will give us negative values for odd n, and positive values for even n.

How can we adjust the formula?

Suggestion:  Divide by -1 to switch all the signs.

Comment:  That will do it.  So will multiplication by -1.  

Note that if we multiply (-1)^n * (n-1)! / x^n  by -1 we get

• -1 * (-1)^n * (n-1)! / x^n ,

which since -1 * (-1)^n = (-1)^(n+1) simplifies to

• f[n](x) = (-1)^(n+1) * (n-1)! / x^n .

We can't use x = 0 with this sequence of derivatives, since every derivative has a power of x in the denominator.

So we shift everything 1 unit to the right, replacing x by x - 1 to obtain

f(x) = f(1) + f ' (1) * (x-1) + f ''(1) * (x-1)^2 / 2! + f '''(1) * (x-1)^3 / 3! + ... + (-1)^(n+1)* (n-1)! (x-1)^n / n! + ... .

A summary is found in the figure below:

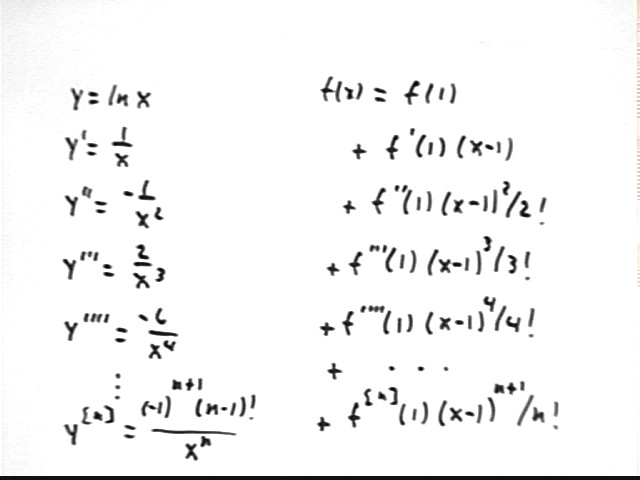
Our values of f and its derivatives at x = 1 are

• f(1) = ln(1) = 0
• f ' (1) = 1 / 1 = 1
• f ''(1) = -1 / 1^2 = -1
• f '''(1) = 2 / 1^3 = 2! / 1^3 = 2
• f '''' (1) = -3 * 2 / 1^4 = -3! / 1^4 = -6
• f ''''' (1) = 4 * 3 * 2 / 1^5 = 4! / 1^5 = 24

and in general, since (n-1)! / n! = (n-1)(n-2)(n-3) ... 1 / [ n (n-1) (n-2) (n-3) ... 1 ] = 1 / n,

• f[n](1) = (-1)^(n+1)* (n-1)! 1^n / n! = -1^(n+1) * 1 / n

So we have

f(x) = ln(x)

= 0 + 1 * (x-1) + -1 * (x-1)^2 / 2! + (2) * (x-1)^3 / 3! + (-3!) * (x-1)^3 / 4! + ... + (-1)^(n+1)* (x-1)^n / n + ...

= (x-1) - (x-1)^2 / 2 + (x-1)^3 / 3 - (x-1)^4 / 4 + (x-1)^5 / 5 ... + (-1)^(n+1)* (x-1)^n / n + ...

This is summarized below:

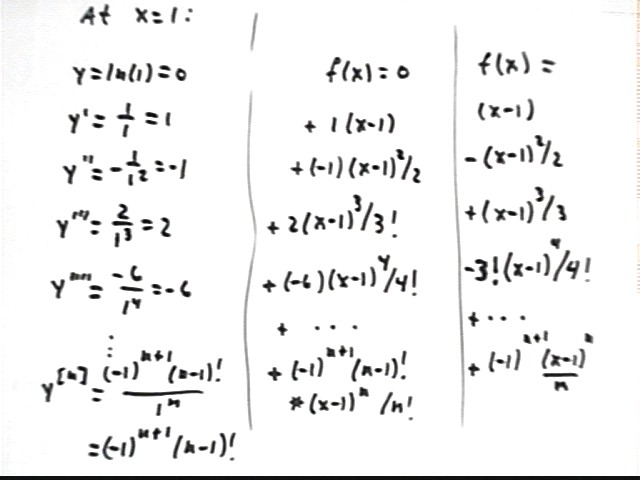
To find the interval of convergence of this sequence we look at limiting value of a(n+1) / a(n).

• a(n+1) = (-1)^(n+1) / n
• a(n) = (-1)^( (n-1) +1) / (n -1) = (-1)^n / (n-1)

Thus

• a(n+1) / a(n) = (-1)^(n+1) / n / [ (-1)^n / (n-1) ] = -1 (n-1) / n = -1 ( 1 - 1/n).

The limiting value of this ratio is therefore

• limit{n -> infinity} | a(n+1) / a(n) | = limit{n ->infinity} |1 - 1/n | = 1.

It follows that the series  (x-1) - (x-1)^2 / 2 + (x-1)^3 / 3 - (x-1)^4 / 4 + (x-1)^5 / 5 ... + (-1)^(n+1)* (x-1)^n / n + ... converges to ln(x) for | x1 | < 1, or 0 < x < 2.

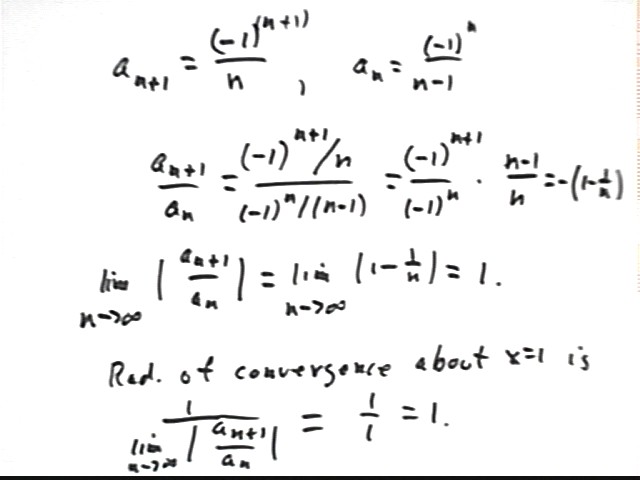
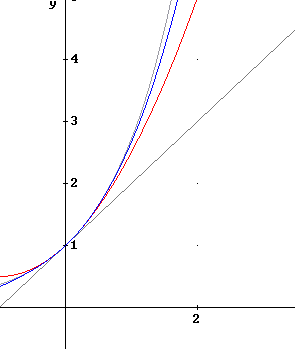
The figure below shows graphs of y = ln(x) and the first-degree Taylor polynomial approximation y = x - 1.

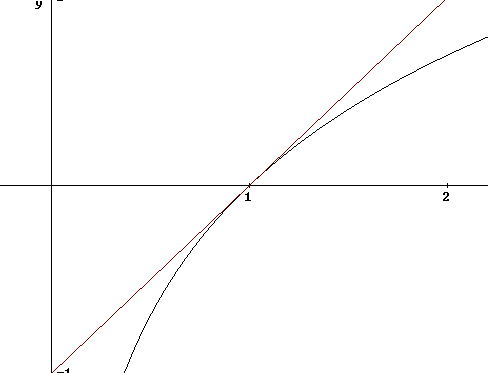
The figure below shows the preceding graphs and the graph of the second-degree Taylor polynomial approximation y = x - 1 - (x - 1)^2 / 2.

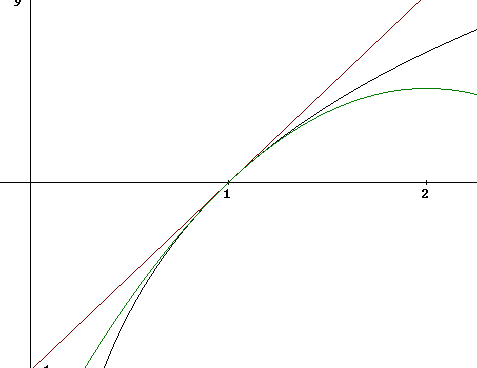
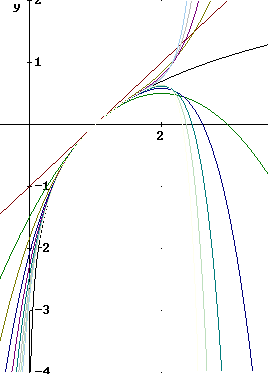
The figure below shows the graphs of y = ln(x) and the graphs of the first- through tenth-degree Taylor polynomial approximations.

• The approximations approach y = ln(x) for 0 < x < 2, as predicted by the analysis of ratios.
• To the left of x = 0 the function y = ln(x) is not defined, so convergence is not possible for x <=0.
• To the right of x = 2 the approximations diverge more and more rapidly, while converging just to the left of x = 2.

The binomial theorem can be proved by performing a Taylor expansion of y = (1 + x )^p at x = 0.

The derivatives of y = (1 + x)^p are

• y ' = p ( 1 + x )^(p-1)
• y '' = p (p-1) (1 + x ) ^(p-2)
• y ''' = p (p-1)(p - 2) (1 + x ) ^(p-3)
• etc.

At x = 0 we get y = 1, y ' = p, y '' = p(p-1), y ''' = p (p-1) (p-2), etc..  The n+1 derivative of y = (1 + x ) ^ p is zero, since (1 + x ) ^ p is a polynomial of degree p.

The Taylor expansion of (1 + x ) ^ p is therefore

• (1 + x ) ^ p = 1 + p * x + p(p-1) * x^2 / 2! + p ( p-1) ( p-2) * x^3 / 3! +  p ( p-1) ( p-2) ( p - 3) * x^4 / 4! + ...  p ( p-1) ( p-2) ... ( p - n + 1) * x^n / n! .

We note that p ( p-1) ( p-2) ... ( p - n + 1 ) / n! = C(p, n), the number of combinations of n objects chosen from among p.