0409

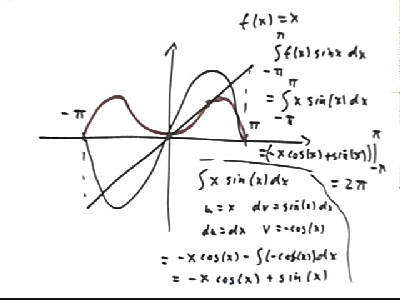
Calculus II Class 04/09

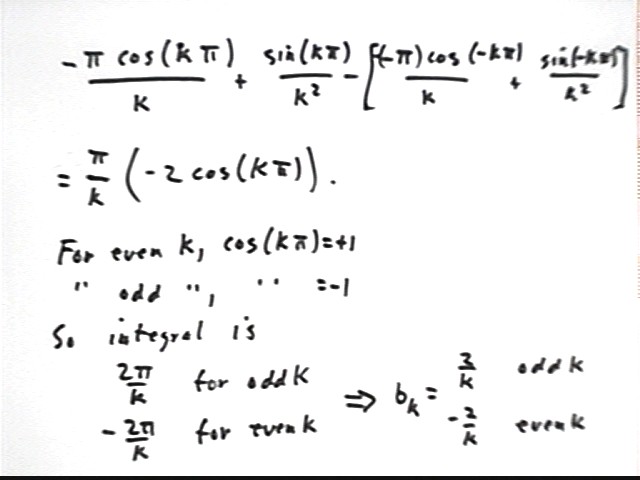
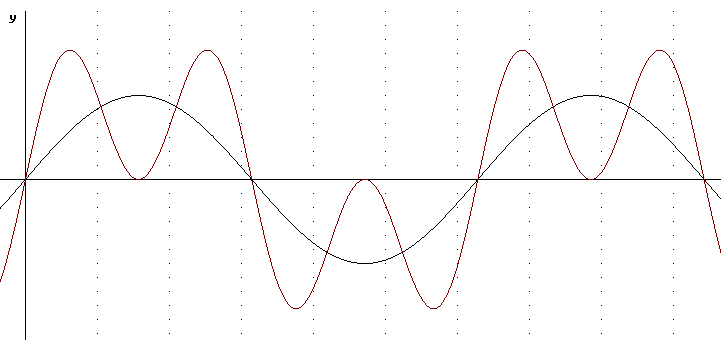
sin(x) doesn't exactly model the square-wave function but it's up at the right times and down at the right times. It just doesn't flatten out at top and bottom as we might wish.

We note that sin(3x) is zero and increasing at every point where sin(x) is zero and increasing, with the same statement possible at every point where sin(x) is zero and decreasing.

sin(x) + sin(3x) doesn't do a whole lot better than sin(x) but it gives us an idea. The problem here is that adding sin(3x) brings us all the way back down to zero in the middle of each cycles of the sin(x) function.

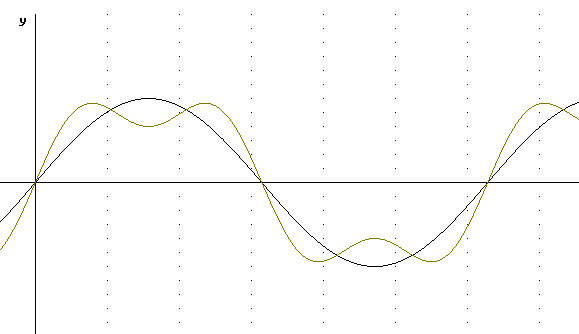
We try sin(x) + sin(3x)/2. This brings us down only about halfway to zero at the midpoint of the first cycle of sin(x), and the peaks are closer to the peak value of sin(x) than in the preceding example.

y = sin(x) + sin(3x) / 3 does even better, staying even closer to sin(x) through each of its cycles.

Find the error in the third-degree Taylor polynomial approximation to sin(pi/3).

Sin(x) = x – x^3 / 3! + x^5 /5! - x^7 / 7! + …

P3(x) = x – x^3 / 3!.

P3(pi/3) = (pi/3) – (pi/3)^3 / 3! = pi/3 – pi^3 / (3^3 * 3!) = pi/3 – pi^3 / 162 = .856.

The actual value of sin(pi/3) is sqrt(3) / 2 = 1.732 / 2 = .866.

Our error is .010.

The figure below depicts the functions y = sin(x) and y = x - x^3 / 3!. The vertical line is at x = pi/3.

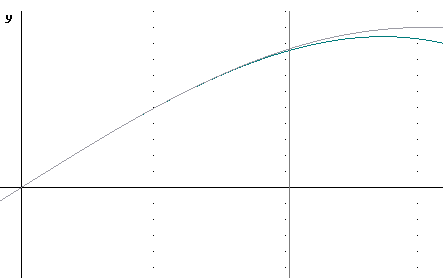
What is the next derivative after the third derivative in the Taylor expansion of sin(x)? How big can this term get between 0 and pi/3?

We got the third term x^3 / 3! by evaluating –cos(x) at x = 0. The next derivative is sin(x). The next term would be sin(x) / 4! * x^4 evaluated at zero for this expansion, so the 4th term does not appear in the expansion. However it’s sorta there in the background, causing errors as we move away from x = 0.

The magnitude of the maximum error possible between x = 0 and x = pi/3 is the maximum possible magnitude of this term between 0 and x = pi/3.

What is the maximum possible value of

· sin(x) / 4! * x^4

between x = 0 and x = pi/3?

Sin(x) and x are both increasing between x = 0 and x = pi/3, so the max value occurs at x = pi/3.

Our max value is sin(pi/3) / 4! * (pi/3)^4 = .0433.

Use this procedure to find the error bound of the third Taylor polynomial approximation to y = e^x when x = .3. Find the actual error and show that it’s within those bounds.

We begin with the third-degree polynomial approximation

P3(x) = x + x^2 / 2! + x^3 / 3!.

Our fourth-degree term is generated by the fourth derivative of x, which is e^x. This gives us the function e^x / 4! * x^4. This ‘background’ function drives the error of the third-degree approximation.

Our error bound is the maximum possible magnitude of this ‘background’ function on the interval in question. Since we have expanded about x = 0 and we’re looking at the approximation for x = .3, we therefore want to find the max possible value of e^x / 4! * x^4 on the interval (0, .3).

This ‘background’ function is formed from the product of two increasing functions e^x and x^4. This means that the function e^x * x^4 / 4! is increasing, and its max value is taken at x = .3.

At x = .3 the value is e^.3 * .3^4 / 4! = . 000456 approx..

The actual value of e^.3 is 1.349858807

The value of P3(x) = 1 + x + x^2 / 2! + x^3 / 3! is P3(.3) = 1.34950000.

The magnitude of the error is the magnitude of the difference between the actual and approximated values, which is .000359 approx..

This is within the max possible error .000456.

What is the term we need in order to estimate maximum possible error of the nth degree approximation to sin(x)?

The n+1 term of the expansion is dictated by the n+1 derivative, which is either +-sin(x) or +-cos(x). The error term is either | sin(x) * x^(n+1) / (n+1)! | or |cos(x) * x^(n+1) / (n+1)! | .

For x = 10, what value of n will ensure that (n+1)! is less than either | sin(x) * x^(n+1) | or | cos(x) * x^(n+1) |?

Since | sin x | <= 1 and | cos(x) | <= 1 we have

| sin(x) * x^(n+1) | < | x^(n+1) | and

| cos(x) * x^(n+1) | < | x^(n+1) | so it will suffice to find n such that | x^(n+1) | < (n+1)!.

Whatever x is, let n be greater than x. Then x^(n+1) < (n+1)^(n+1).

But (n+1)^(n+1) =(n+1) * (n+1) * (n + 1) * … * (n + 1), where we have the factor n+1 a total of n+1 times.

(n+1) ! = (n+1) * n * (n-1) * (n-2) * … * 1.

This expression consists of n+1 terms, each less than the corresponding (n+1) term of (n+1)^(n+1).

This does not establish that (n+1)! is greater than (n+1)^(n+1).

So let n > 2 x. We now have x < n/2 so x^(n+1) < (n/2)^(n+1). Now we have n/2 * n/2 * n/2 * … * n/2, where the factor n/2 is multiplied n times.

(n+1) ! = (n+1) * n * (n-1) * (n-2) * … * 1.

So x^(n+1) / (n+1)! < [n/2 * n/2 * n/2 * … * n/2 ] / [ (n+1) ! = (n+1) * n * (n-1) * (n-2) * … * 1 ]

= (1 / 2)^(n+1) * n / (n+1) * n / (n) * n / (n-1) * … * n / 1.

Now if we increase n by 1 we get another factor of 1 / 2 , and we get the term (n+1) / (n+2).

Since (n+1) / (n+2) < 1, our new expression is less than 1 / 2 of the previous expression.

We can therefore make our expression as small as we wish by increasing n.