Calculus II Class 04/16

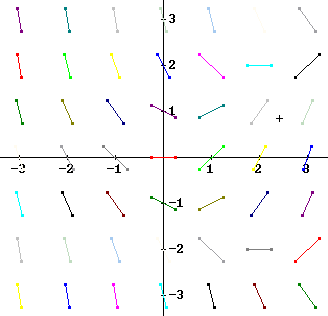
Sketch the slope field of the equation dy/dx = x - y^2/2 for x = 1 and 2 and y = -1, 0 and 1.

Sketch the slope field for -3 < x < 3 and -3 < y < 3.

For x = 1, y = 1 we get slope = dy/dx = 1 - 1^2 / 2 = 1/2, so at (1, 1) we sketch a segment with slope 1/2.

For x = 2, y = 1 we get slope = dy/dx = 1 - 1^2 / 2 = 3/2, so at (1, 1) we sketch a segment with slope 3/2.

These two segments are shown in the figure below.

At (1, 2) the slope will be 1 - 2^2/2 = -3 and at (2, 2) the slope will be 2 - 2^2/2 = 0.

At (1,-1) and (1, -2) the slopes will be the same as at (1, 1) and (1, 2), due to the fact the y^2 is the same for positive or negative y.

From the last observation we conclude that the field will be symmetric with respect to the x axis. 

We also see that moving left or right one unit will raise or lower the slope by one unit.

Using these patterns, and extending to y = 3, we can sketch the second slope field shown below.

Follow the slope field of the equation

dy/dx = sqrt(y)

to estimate where you would end up if you started at (1, 1) and moved along the field until you had moved 1 unit in the x direction, then from that point another unit in the x direction.

Solve the equation dy/dx = sqrt(y).

Sketch a grid with short line segments, called 'slope segments', at every point on the grid we get when we intersect the lines x = 0, 1, 2, 3 with the lines y =  0, 1, 2, 3 (i.e., the points (0, 0), (0, 1), ... (0, 3), (1, 0), (1, 1), ..., (1, 3), (2, 0), etc.).    The slope of each segment should be y / 2, where y is the y coordinate of the point.

We get the figure below.  The curves represent possible paths within the slope field.

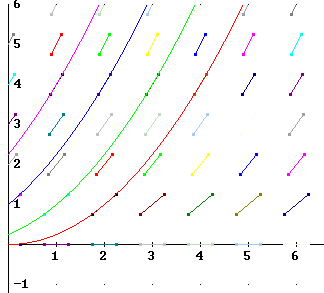
On what line or curve will we have slope segments with slope  1?

On what line or curve will we have slope segments with slope  2?

What will be the slope along the line y = c, where c is any constant number?

Since the slope is dy/dx = sqrt(y) we will have slope 1 where sqrt(y) = 1.  This occurs when y = 1, so slope 1 occurs at all points of the line y = 1.  The figure below shows this line with slope segments of length 1 sketched along the line.

Slope 2 occurs where sqrt(y) = 2.  This occurs when y = 2^2 = 4.  So everywhere on the line y = 4 the slope would be 2.

Along the line y = c the slope is dy/dx = sqrt(y) = sqrt(c).  Note that this can occur only if y is not negative.  If y is negative the slope field is not defined and no solution curve can extend to negative y values.

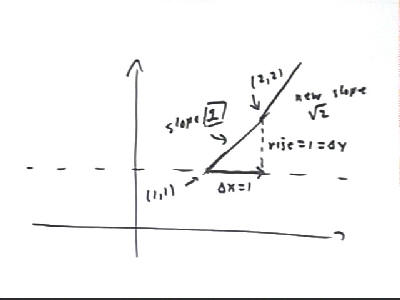
The point (1, 1) lies on the line y = 1, and so the slope at (1, 1) is 1.  At what point do we arrive if we follow a line of this slope while x changes by 1 unit?

If x changes by `dx = 1 unit then y will chage by `dy = slope * `dx = 1 * 1 = 1.

Moving `dx = 1 unit and `dy = 1 unit from (1, 1) gets us to the point (1 + `dx, 1 + `dy) = (1+1, 1+1) = (2,2).

What is the slope at the point (2, 2)?  What point to we obtain if we follow a line of this slope from (2, 2) until x has changed by 1 unit?

At (2, 2) the slope is dy/dx = sqrt(y) = sqrt(2) = 1.414 approx..

If x changes by `dx = 1 unit then y will chage by `dy = slope * `dx = 1 * sqrt(2)   = sqrt(2) = 1.414 approx..

Moving `dx = 1 unit and `dy = 1.414 unit from (1, 2) gets us to the point (1 + `dx, 2 + `dy) = (1+1, 1+1.414) = (2,3.414).

Solve the equation dy/dx = sqrt(y) to obtain y as a function of x.

If we change the form of the equation to

dy/sqrt(y) = dx

then we can integrate both sides to obtain

2 sqrt(y) = x + c,

where we have placed the arbitrary constant of integration on the right-hand side.

To solve for y we first divide both sides by 2 then square the result to obtain

y = (x/2 + c)^2.

Note that we don't bother dividing the c by 2 because c was originally an arbitrary constant, meaning that c could be any real number at all.  Since it follows that c / 2 could then be any real number, we can still write it as just c.

Note that (x/2 + c) could be written as 1/2 (x + c), where again the constant just 'absorbs' the arithmetic operation on it.  Then the square of (x/2 + c) woud be the square of 1/2 (x + c) , or 1/4 (x+c)^2.

The curves y = 1/4 (x + c)^2 consist of the y = x^2 curve vertically stretched by factor 1/4 then shifted c units to the left.  This gives us a series of 'squashed down' parabolas with vertices along the x axis.  Every point of the x axis will be a vertex, with positive values of c corresponding to vertices on the negative x axis and negative values of c corresponding to vertices along the positive x axis.

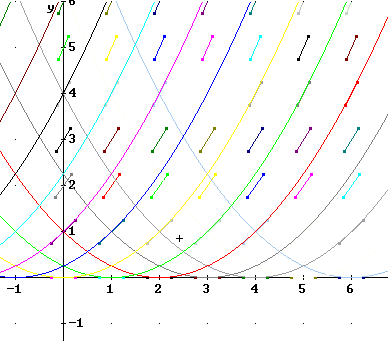
Some of these curves were shown in a previous figure along with the direction field.   The figure is shown again below.

The curves are the graphs of the functions y = 1/4 (x+c)^2 for c = 0, 1, 2 and 3.

A more extensive set of curves y = 1/4(x+c)^2 is shown below.  The c = -1, -2 and -3 curves, for example, have vertices at (1,0), (2,0) and (3,0).

• It is clear that some parts of these curves fit the slope field while other parts do not.
• A closer look shows that the increasing part of each curve fits the slope field, while the decreasing part does not.

Note also that two of these curves intersect at (1, 1).  Be sure you can see which of these two curves follows the slope field in the vicinity of (1, 1).

Which of the curves y = 1/4 (x+c)^2 passes through the point (1, 1)?

If we plug x = 1, y = 1 into the form y = 1/4 (x+c)^2 we get 1 = 1/4 ( 1 + c)^2.

We solve this equation for c by multiplying both sides by 4, then taking + or - the square root of both sides to get

+- sqrt(4) = 1 + c.

This gives us the two equations

1 + c = 2

1 + c = -2

with solutions c = 1 and c = -3.

A sketch of both the y = 1/4 (x + 1)^2 curve and the y = 1/4 (x - 3)^2 curves shows us that only the c = 1 solution matches the slope field, so we reject the c = -3 solution.

When we followed the slope field one x unit at a time from (1, 1) we arrived at the point (3, 3.414).  We knew that the slope field was actually curving up and away from each of our line segments and that our result is only an approximation to the y value we obtain if we start at (1, 1) and move 2 units to the right.  The curve we just found, y = 1/4 ( x + 1)^2, gives us the accurate path if we start from (1, 1).  According to this curve what is the value of y when x = 3?  How does this compare with our approximation?

The x = 3 value is found by plugging x = 3 into y = 1/4 (x+1)^2 to obtain

y = 1/4 * (3 + 1)^2 = 1/4 * (4^2) = 1/4 (16) = 4.

Our approximation y = 3.4 is fairly close to 4, considering that our x values 'jumped' by 1 unit with each step of the approximation.

>