Calculus II Class 04/21

Solve the equation dz/dy = yz with initial condition z=1 when y=0.

The figure below shows the solution.  This solution follows the pattern of solutions seen in previous notes:

• We first separate the variables, getting all expressions involving z on one side and all expressions involving y on the other.
• We then integrate both sides.
• The equation we get is in terms of ln | z | .  We use the properties of exponential and natural log functions to solve the equation for z.

Our final result is z = A e^(y^2/2), with A nonzero.

We continue by evaluating the constant A for the given conditions, substituting z = 0 and y = 0 and obtaining A = 1.

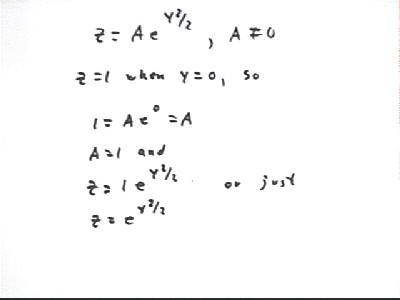
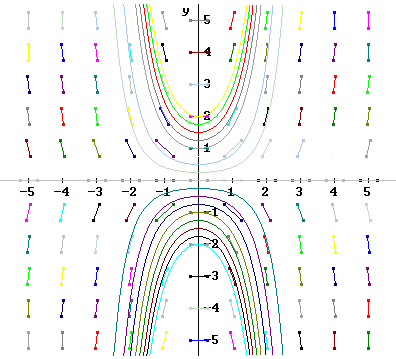
The figure below shows the direction field and the solutions y = A e^(y^2/2) for A = -2, -1.75, -1.5, ..., 1.75, 2.

Quick review of steps in integration by u substitution:

1.  Let u equal something in the integral.  Try different possibilities until you get used to what you need to look for

• e.g., integrating x sin(x^2) dx we could try u = x, u = sin(x^2), u = x^2 or even u = x sin(x^2).  The one that ends up working is u = x^2).

2.  Find du/dx (assuming variable is x; otherwise use whatever the variable is).

• e.g if u = x^2 then du / dx = 2x .

3.  You get du/dx = something so du = something * dx.

• e.g. if du/dx = 2x then du = 2 x dx.

4.  Hopefully some constant multiple of that something * dx appears in your integral.

• e.g. our original expression x sin(x^2) dx contains x dx, which appears with a constant in du = 2x dx.

5.  Solve du = something * dx for whatever you've got in your integral, letting any constants go over there with the du.

• e.g. if du = 2 x dx and our integral contains x dx we get x dx = du / 2

6.  See if you can rewrite your entire integral in terms of u.

• x sin(x^2) dx = sin(u) * du / 2.

7.  Integrate if possible.

• integrating sin(u) du / 2 we get - cos(u) / 2 + c.

8.  Substitute back for u

• -cos(u) / 2 + c = -cos(x^2) + c.

Solve the equation dw/d(theta) = w^2 theta sin(theta^2) with initial condition w(0) = 1.  One of the integrals you must perform involves substitution.   If you don't understand all the steps you should go back to the summary given above and fill in every step you do not understand.

We follow the same method of solution outlined above.  When we integrate we will require substitution to evaluate the integral on the right-hand side.

Our solution is w = 1 / (1/2 cos(theta^2) + c).  Better form is w = 2 / (cos(theta^2) + c), which is not shown below.

Using the first form, when we substitute the initial condition w(0) = 1 we find that c = 1/2.  Note that if we used the other form of the solution we would get c = 1.

Solve dQ/dt = b - Q.

We separate variables as shown.

The integral of dQ / (b-Q) is done by substituting u = b - Q.  If necessary fill in the steps of this integration by substitution.

The result is Q = b + A e^t, where A is a nonzero constant.

Note that much of the class was spent on the mechanics of integration and at time differentiation.  Please review the material on integration technique and if necessary on differentiation so these techniques do not interfere with your understanding of the topics covered in the present sections.  If it takes you over a minute to perform any of these integrations, or over 20 seconds to perform any required differentiations, you need to practice.