Calculus II Class 04/23

1 liter of pure Coke, hole in bottom of container, .1 liters exit per second, balanced by .1 liter per second inflow of pure water.

Estimate how much Coke and how much water will be in the container after the first 10 seconds.

Based on your previous estimate estimate how much of each will be in the container after another 10 seconds.

Crude estimates:

In 10 seconds we mix a liter of water with a liter of Coke and drain off 1 liter of the mixture.  We end up with 1 liter of solution, 1/2 liter of which is Coke.

In the next 10 seconds we mix a liter of water with a liter solution containing 1/2 liter of Coke, then drain off half of the mixture.  This leaves us with 1/4 liter of Coke.

According to this model the concentration of Coke will go down by half every 10 seconds.  The amount of Coke at 10-second intervals will be a geometric series with common ratio 1/2, and the concentration will be an exponential function of clock time.

Do you believe that this model is accurate?  Why or why not?

The model isn't particularly accurate.  If we add the 1 liter before draining off any liquid the concentration changes in 1 instant, whereas with a continuous inflow and outflow the concentration of the outflowing liquid changes continuously.  There is no reason to expect the two to give the same overall model.

If the concentration of Coke in the bottle at a given instant is C(t).  (Concentration is amt of Coke / amt of mixture.)  Then in a short time `dt near clock time t how much water and how much Coke flows out of the bottle.

In time interval `dt the amount of water flowing into the bottle is .1 liter/sec * `dt, and the amount of mixture flowing out of the bottle is .1 liter/sec * `dt.

In the .1 liter/sec * `dt of mixture that flows out during time interval `dt, the amount of Coke flowing out is

• amt of Coke flowing out = concentration * amt of mixture flowing out

or

• amt of Coke flowing out = C(t) * (.1 liter/sec * `dt).

By how much does the concentration therefore change in time interval `dt?

We had 1 liter of solution with concentration C(t), so the amount of Coke was C(t) * 1 liter.

We lost C(t) * (.1 liter/sec) * `dt so our amount of Coke is now

• new amt = C(t) * 1 liter - C(t) * .1 liter/s * `dt.

The new concentration is therefore

• new concentration = [C(t) * 1 liter - C(t) * .1 liter/s * `dt] / (l liter) = C(t) - C(t) * .1 / s * `dt.

What is the ave rate at which concentration is therefore changing during `dt?

Change in concentration is `dC = C(t) * .1 / s * `dt, which takes place in time interval `dt so the rate of change is

• `dC / `dt = -C(t) * .1 / s * `dt / `dt = -C(t) * .1 / s.

What differential equation does this give us?

Taking the limit at `dt -> 0 we get

• dC / dt = -.1 C.

Init concentration is 100% = 1 so C(0) = 1.

Follow the same process but for inflow rate .05 liter/sec and outflow rate .10 liter/sec.

Let C(t) stand for the concentration, which is amt of Coke / amt of mixture.

At clock time t (assume units of liters and seconds) we will have lost .1 t and gained .05 t of solution.  Since we started with 1 liter our total amount of solution is therefore

• amt of soln at clock time t:  amt =

  1 + .05 t - .1 t

In time interval `dt amount of mixture leaving the container is .1 `dt, which carries off an amount of Coke which is equal to C(t) * amount leaving = C(t) * .1 `dt (as before concentration * amt of soln = amt of Coke).

So the change in the amount of Coke is - C(t) * .1 `dt.  The amount of solution at clock time t is  1 - .05 t + .1 t, containing amount C(t) * (1 + .05 t - .1 t) of Coke.  The new amount of Coke will be

• new amt of Coke = C(t) * (1 + .05 t - .1 t) - C(t) * .1 `dt.

The change in concentration is change in amt of Coke / volume, which is

• `dC = -C(t) * .1 `dt / (1 + .05 t - .1 t)

so that

• `dC/`dt = .1 C(t) / (1 + .05 t - .1 t),

giving us the differential equation

• dC/dt = .1 C / (1 + .05 t - .1 t)

or simplifying the denominator

• dC/dt = .1 C / (1 - .05 t).

Suppose a population grows in proportion to population when it has plenty of room, but as it approaches its 'carrying capacity' the rate decreases.

Unchecked population growth is modeled by

• dP/dt = k P,

rate of change proportional to population.

A model of limited population growth is

• dP/dt = k P ( L - P).

L is called the 'carrying capacity'.  When population reaches this level dP/dt will be zero.

from before Solve the equation dz/dy = yz with initial condition z=1 when y=0.

The figure below shows the solution.  This solution follows the pattern of solutions seen in previous notes:

• We first separate the variables, getting all expressions involving z on one side and all expressions involving y on the other.
• We then integrate both sides.
• The equation we get is in terms of ln | z | .  We use the properties of exponential and natural log functions to solve the equation for z.

Our final result is z = A e^(y^2/2), with A nonzero.

We continue by evaluating the constant A for the given conditions, substituting z = 0 and y = 0 and obtaining A = 1.

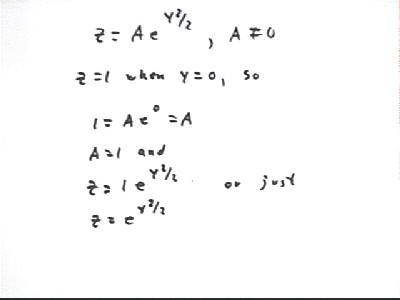
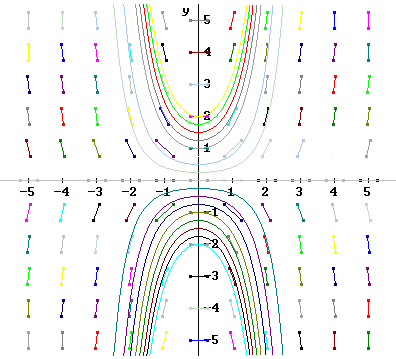
The figure below shows the direction field and the solutions y = A e^(y^2/2) for A = -2, -1.75, -1.5, ..., 1.75, 2.

Quick review of steps in integration by u substitution:

1.  Let u equal something in the integral.  Try different possibilities until you get used to what you need to look for

• e.g., integrating x sin(x^2) dx we could try u = x, u = sin(x^2), u = x^2 or even u = x sin(x^2).  The one that ends up working is u = x^2).

2.  Find du/dx (assuming variable is x; otherwise use whatever the variable is).

• e.g if u = x^2 then du / dx = 2x .

3.  You get du/dx = something so du = something * dx.

• e.g. if du/dx = 2x then du = 2 x dx.

4.  Hopefully some constant multiple of that something * dx appears in your integral.

• e.g. our original expression x sin(x^2) dx contains x dx, which appears with a constant in du = 2x dx.

5.  Solve du = something * dx for whatever you've got in your integral, letting any constants go over there with the du.

• e.g. if du = 2 x dx and our integral contains x dx we get x dx = du / 2

6.  See if you can rewrite your entire integral in terms of u.

• x sin(x^2) dx = sin(u) * du / 2.

7.  Integrate if possible.

• integrating sin(u) du / 2 we get - cos(u) / 2 + c.

8.  Substitute back for u

• -cos(u) / 2 + c = -cos(x^2) + c.

Solve the equation dw/d(theta) = w^2 theta sin(theta^2) with initial condition w(0) = 1.  One of the integrals you must perform involves substitution.   If you don't understand all the steps you should go back to the summary given above and fill in every step you do not understand.

We follow the same method of solution outlined above.  When we integrate we will require substitution to evaluate the integral on the right-hand side.

Our solution is w = 1 / (1/2 cos(theta^2) + c).  Better form is w = 2 / (cos(theta^2) + c), which is not shown below.

Using the first form, when we substitute the initial condition w(0) = 1 we find that c = 1/2.  Note that if we used the other form of the solution we would get c = 1.

Solve dQ/dt = b - Q.

We separate variables as shown.

The integral of dQ / (b-Q) is done by substituting u = b - Q.  If necessary fill in the steps of this integration by substitution.

The result is Q = b + A e^t, where A is a nonzero constant.

Note that much of the class was spent on the mechanics of integration and at time differentiation.  Please review the material on integration technique and if necessary on differentiation so these techniques do not interfere with your understanding of the topics covered in the present sections.  If it takes you over a minute to perform any of these integrations, or over 20 seconds to perform any required differentiations, you need to practice.