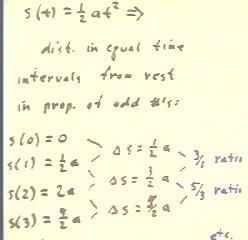Calculus II

Class Notes, 1/20/99

We show that if acceleration is constant and we start from rest, the distance traveled is proportional to the square of the time:

• Constant acceleration implies that dv / dt = constant; starting from rest implies that v(0) = 0.
• The solution to the resulting differential equation is v = constant * t + c; the initial condition implies that c = 0.
• We therefore conclude that velocity is v(t) = constant * t.
• This is a proportionality; velocity is proportional to time.

We solve the differential equation for the distance function s(t):

• The equation is ds / dt = v(t) = constant * t; it is obvious that s(0) = 0.
• The general solution to the differential equation is s(t) = constant * t^2 + c (note that the constant in this solution is half as great as that in the equation itself).
• The initial condition implies that c = 0, so our distance function is s(t) = constant * t^2.
• Thus our distance function is proportional to the square of the time.

We show that when the position function is s(t) = 1/2 a t^2, the distances traveled in successive 1-unit time intervals are in the ratio of the odd numbers.

• We evaluate s at t = 0, 1, 2, 3, . . ..
• We find the differences between these results, obtaining the distances traveled during succesive seconds.
• We see that the ratios of the distances are 3/1, 5/3, . . ..
• We can see also that the distance traveled in the second interval is 3 times that traveled in the first, the distance in the third is 5 times that traveled in the first, etc..