Calculus II
Class Notes, 2/03/99
We will compare the left, right, and trapezoidal
approximations and actual integral of y = ln(x/2).
- We first observe that since the function,
whose graph is as shown below, is strictly increasing, the left
approximation will be less than any of the others, the right
approximation will be greater, and a trapezoidal approximation will
lie between the left and right approximations.
- We observe also that since the graph
is concave downward, the region under the curve
will always curve up and over the chord at
the top of the trapezoid.
- We conclude that the actual
integral will always be greater than the trapezoidal
approximation.
- We therefore predict that
the numerical results, listed in increasing order, will
be left < trapezoidal < right < actual.
We proceed to calculate the values of the integral
and of the n = 3 approximations for x = 2 to x = 11.
The same techniques will be used and the same ordering will
be obtained for the original interval x = 2 to 20; you should complete
these calculations.
- We divide the interval from x = 2 to x = 11, whose
length is 9, into 3 subintervals each of length 3.
- The DERIVE vector command vector( [x, log(x/2) / log(2) ], x,
2, 11, 3) will give a table of y vs. x values.
(Note error: in the figure, the x before the 2, 11, 3 is missing).
- DERIVE could be used to calculate any of the approximations or the actual integral as
follows:
- The DERIVE command vector ([log(x/2)], x, 2, 11, 3) will give a
single-column listing of the values.
- The DERIVE command sum (vector ([log(x/2)], x, 2, 11, 3) ) will give a sum
of these values.
- The DERIVE command 3 * sum (vector ([log(x/2)], x, 2, 8, 3) ) will give
the left approximation.
- The DERIVE command 3 * sum (vector ([log(x/2)], x, 5, 11, 3) ) will
give the right approximation.
- The DERIVE command 3 * sum (vector ([log(x/2) + log(x+3) / 2], x, 5, 8, 3) ) will
give the trapezoidal approximation.
- The DERIVE command 3 * sum (vector ([log(x/2)], x, 3.5, 9.5, 3) ) would
give the midpoint approximation.
- The DERIVE command int( log(x/3), x, 2, 11) would give the actual
integral.
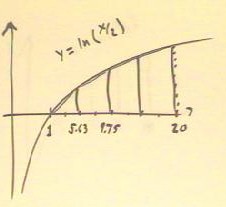
The graph below depicts the values of the function
at x = 2, 5, 8 and 11.
The 'left' altitudes will occur at x = 2, 5, and 8, and
each will be multiplied by the 3-unit width of the
corresponding interval to get the left approximation. The results are
shown in the figure.
The 'right' altitudes will occur at x = 5, 8 and 11, and
the results are shown.
The 'averages' of left and right altitudes, used for the trapezoidal
approximation, are .46, 1.16 and 1.55; each is multiplied
by the width of its interval to obtain the trapezoidal
approximation, as indicated.
The integral is easily calculated using either integration
by parts or a table.
We see that, as expected, the left approximation is the smallest,
the right the largest, and the trapezoidal
approximation is less than the actual integral.
The figure below shows why when a function is increasing the
left approximation is low and the right is
high.
Similarly if the function is decreasing we conclude that the right
approximation is low and the left high.
The figure below shows how the error of the left approximation
changes as the width of the interval is
halved.
- Note that for sufficiently small intervals, each region under
the graph will be an approximate trapezoid.
- The left error for each trapezoid is the area of
the triangle at the top of the trapezoid.
- When the width of a trapezoid is halved, both the base
and the height of the 'error triangle' are halved
so that the left error becomes 1/4 as great.
- When a trapezoid is subdivided into two
trapezoids, then, each of the two trapezoids will
have approximately 1/4 the error of the original
so that the total error will be 2 * 1/4 as great,
or 1/2 as great.
- This argument makes it very plausible that the left-hand error of
the approximation is inversely proportional to the number
of divisions, to the extent that the number of divisions is large
enough that each subregion is in approximate trapezoid.
- A very similar argument where we subdivide each trapezoid into
n subregions would prove this proportionality.
- One result is that therefore if we use 10 times as
many subdivisions, our error is reduced by
a factor of 10 and we obtain an extra decimal place in
the accuracy of our approximation.
For a trapezoidal approximation, the error is the small
'crescent' between the top of the trapezoid and
the actual curve.
The second derivative and the width of the interval determine
how much the actual curve arcs above or below
the trapezoid.
- If the arced region above the trapezoid is regarded as an approximate
triangle, then width of the interval and the difference
between the actual slope at the left and the right
end of the trapezoid determines the altitude of
the triangle.
- If the width of the trapezoid is halved, the difference
in the slopes will be cut in half, and the difference
will apply over only half the distance, so the altitude of
the 'triangle' will be only 1/4 as great.
- Since the 'triangle' will have only 1/4 the altitude and
1/2 the width its area will be only 1/8
as great.
- Thus when a trapezoid is subdivided into two trapezoids,
each of the two will have only 1/8 the error of the original
and the total error of the two will be 2
* 1/8 = 1/4 as great as before.
- 1/4 is the square of 1/2, the proportion
by which we reduced the width.
- We therefore see the plausibility of the argument that the error
of the trapezoidal approximation is inversely
proportional to the square of the the number of
divisions, or proportinal to the square of the width.
- If the proportionality holds, then 10 times as many divisions would
result in 1/10^2 = 1/100 the error and our accuracy would
therefore improve by two decimal places.
- Note that 10 times the number of divisions for the left
approximation gave us just 10 times the accuracy,
or 1 decimal place improvement, whereas the same change for
a trapezoidal approximation gave us 100 times the accuracy
and a 2 decimal place improvement.
- We get 100 times the improvement for 10 times the
work by using the trapezoidal approximation as opposed
to the left approximation.
