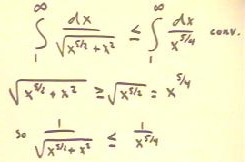Calculus II
Class Notes, 2/10/99
Since `sqrt( x^(5/2) + x^2 ) > = `sqrt(x^(5/2)) = x^(5/4), we
see that 1 / `sqrt( x^(5/2) + x^2 ) < = 1 / x^(5/4), which is 1 / x^p
for p > 1 and therefore converges.
- It follows that the integral in the figure below converges, as
indicated.
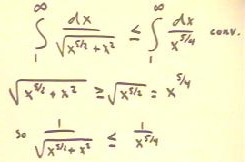
To see that the integral in the figure below converges, we observe that the numerator
must lie between 1 and 7, as shown by the graph
of the numerator (model by a reference circle of radius three
centered at y = 4, as indicated).
- It follows that the given integral is bounded above by the integral
of 7 / `theta^3, which is clearly convergent (with
denominator `theta ^ p, p > 1).
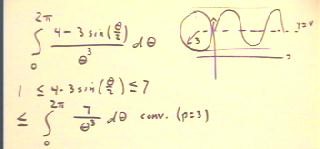
To find an upper bound for the given integral of e^(-x^2),
we note that since for x > = 1 we have x^2 > = x,
then for x > = 1 we have e^(x^2) > e^x and
therefore e^-(x^2) < = e^(-x).
- Then since the integral of e^-x for the given limits
is e, we see that the given integral of e^-(x^2) must converge.
We can generalize this result, as shown in the lower
right-hand corner, to show that the integral of e^(-x^2)
from a to infinity must be < =
e^(-a^2) / a.
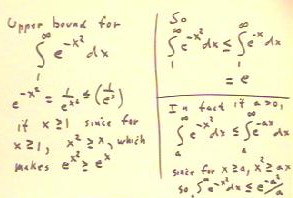
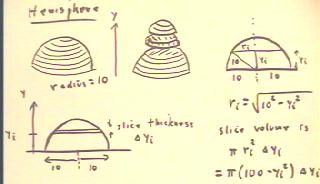
We can determine the volume of a hemisphere of radius
10 by first determining the approximate volume of a horizontal
slice with thickness `dyi near altitude yi.
- The approximate volume will be the product of the cross-sectional
area of the slice as determined at yi and its thickness.
- The figure at lower left depicts the slice.
- The figure at upper right shows how we can use right
triangles to determine the radius of the cross-section at
height yi.
- The approximate volume of the slice will therefore be as indicated at lower
right.
The total volume of the slices will be the sum of all
such slices, indicated by the sum in the figure below.
- The values of yi range from 0 to 10.
- In the limit the integral therefore approaches
that shown in the last line of the figure.
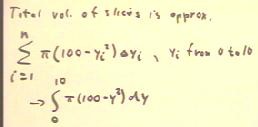
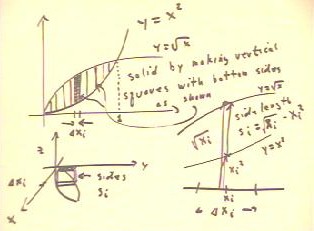
To find the volume of the solid created above the region bounded
by the curves y = x^2 and x = `sqrt(x), with the property that each
cross-section parallel to the y axis is a square whose base is
the segment between the curves, we proceed as in the figure below.
- The sketch at lower left depicts the cross-section of the solid on interval
i.
- The volume of the cross-section will be approximately equal to the area
of the indicated square and the thickness `dxi.
- To find the length si of the side we use the sample point xi within
the ith interval, where the distance from the x axis to the lower curve is
xi^2 and to the higher curve is `sqrt(xi).
- The side si extends from the lower curve to the upper and hence has
length `sqrt(xi) - xi^2.
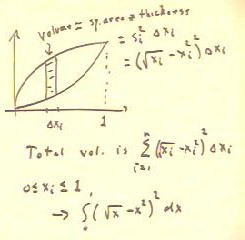
The volume lying above the strip indicated
in the figure below is therefore the product si^2 `dxi = (`sqrt(xi)^2 - xi^2)
`dxi, as indicated below.
- The total volume is obtained by summing over all
such strips, where xi ranges from 0 to 1.
- We therefore obtain the integral indicated at the bottom of
the figure below.
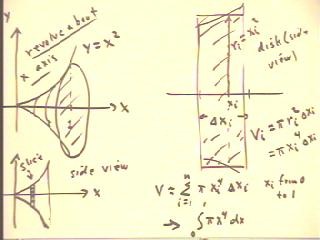
We can rotate the portion of the curve y = x^2 from x
= 0 to x = 1 about the x axis, obtaining the horn-shaped
solid indicated below.
- We find the volume of this figure by finding the approximate
volume of the typical slice of the figure.
- The slice will be a disk with beveled edges;
if the slice is sufficiently thin the difference in cross-sectional
areas over an individual slice will be small, so the we can approximate
the slice by a uniform disk.
- The volume of the disk will be the product of the area of
its circular cross-section and its thickness.
- An enlarged view of the ith slice is shown at upper right in
the figure below.
- xi is the arbitrary point within the interval at which
we determine the radius of the slice, which we will then
be used to find the area of the corresponding circular cross-section of
the disk.
- The radius will equal the value xi^2 of the function
at xi.
- The volume of the disk will therefore be `pi ri^2 `dxi = `pi
xi^4 `dxi.
- The total volume will be approximately equal to the sum indicated
at bottom right, where xi range from 0 to 1.
- The sum approaches the specified integral.