Video Clip #01
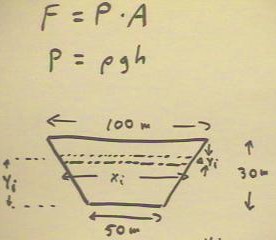
The force on the
hemispherical dam in the figure below is calculated in an analogous
manner.
- As before we find the area
of a horizontal strip of thickness `dyi; this
time we measure yi from the level of the water at the top
of the dam.
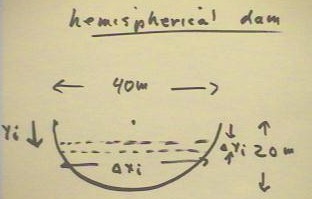
The width xi of the strip is calculated by first using the Pythagorean
Theorem to determine half the width, as indicated in the figure below.
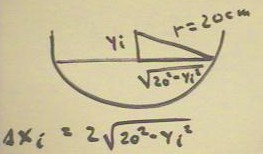
The area Ai will be the product of the width and
the thickness of the strip, as indicated below.
- The pressure Pi will be simply `rho g yi, since yi as
measured from the water level is the depth.
- The force Fi will be the indicated product of area
and pressure.
- The Riemann sum of the force contributions Fi is
indicated in the next-to-last line below, where yi takes values between 0 and 20, and the
resulting integral in the last line.
- The integral is easily evaluated using the substitution u = 400 - y^2; the result is the
total force on the dam.
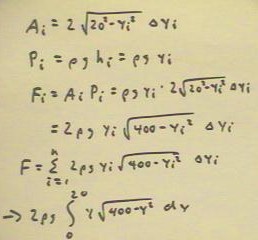
Video Clip #02
We next determine the velocity required for a small satellite near
its surface to completely escape the gravitational attraction of a 1.2
kg pendulum bob of radius 5 cm.
- It is easiest to picture this problem with the spherical bob in empty space,
far away from the gravitational influence of the rest of
the universe.
- The gravitational attraction of the sphere is quite small, so the velocity
required probably will be small.
- To escape the gravitational field of the sphere, the
satellite must have a kinetic energy 1/2 m v^2 equal to the work
done by the satellite against the gravitational pull of
the sphere as it travels from the surface of the sphere
to an infinite distance from the sphere.
We begin by calculating the work done against gravity as
the satellite moves through distance `drI directly away from the sphere,
while at approximate distance ri.
- The work is the product of the force and the distance;
the force is determined by the gravitational attraction F = G M m
/ r^2, where M is the mass of the sphere and m the mass of the satellite.
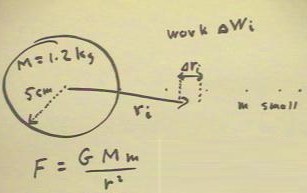
The work contribution over the interval will be as indicated below.
- The total work will be approximated by a Riemann
sum of the Wi contributions, which in the limit gives
us the indicated integral for the work Wesc done against
gravity by the escaping satellite.
- The integral is easily evaluated, with the indicated result.
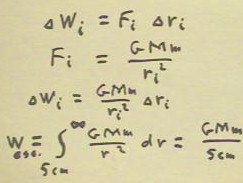
Substituting the values of G and the 1.2 kg mass M
of the sphere, we obtain Wesc = 1.4 * 10^-9 J / kg * (m), where
(m) is the mass of the satellite.
- We set this equal to the kinetic energy KE0 at the surface.
- Using 1/2 (m) v^2 for the kinetic energy, we easily solve
for v.
- We might have symbolically solved the equation 1/2 (m) v^2 = G
M m / R for v, then substituted G, M and R = 5
cm - .05 m for the resulting expression v = `sqrt( 2 G M / R ).
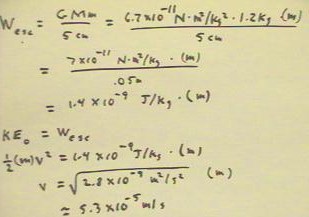
Video Clip #03
We calculate the kinetic energy of a uniform 50 cm rod
rotating with an angular velocity of .5 rad/s about
its center.
- We begin by calculating the kinetic energy of the segment of
length `dx at position xi as measured from the center of
rotation.
- The mass per unit of length will be 40 g / 50 cm, so a
segment of length `dx will have mass mi = 40/50
(g / cm) `dxi.
- The velocity of a segment at distance xi from the center
of rotation will be the product vi = .5 rad/s * xi of its angular
velocity and distance from the center.
- The kinetic energy of the segment is therefore 1/2 mi vi^2,
which when we substitute mi and vi simplifies to .1
xi `dxi.
- The total kinetic energy is therefore the Riemann sum of
the KEi contributions, with xi ranging from -25
cm to 25 cm (positions on the rod as measured with respect to its center).
- The Riemann sum approaches the indicated integral,
which is easily evaluated.

Video Clip #04
We finally calculate the work required to lift the fluid
from a uniform cylinder, initially filled to depth 20 cm, to
a reservoir 15 cm above the initial level of the fluid.
- We begin by calculating the work required to lift the fluid
in a horizontal strip of width `dyi at altitude
yi above the bottom of the container.
- The work will be the product of force and
distance.
- The force in this case is the weight `rho g Vi of the
fluid in the strip, where Vi is the volume of the strip.
- The distance hi is the vertical distance from the strip
to the reservoir 15 cm above the initial fluid level.
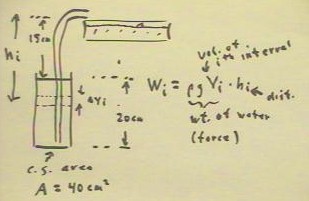
You should complete the process of finding and
evaluating the associated integral.
- The integral should be of the expression `rho g A (35 - y) dy,
where A = 40 cm^2; y should run from 0 to 20 cm.
- `rho g A dy represents the force while (35
- y) represents the distance through which the force is applied.
Video Clip #05