Assignment 19

1.  Find the second derivative of each function:

a.  f(x) = x^2 _ 7 x - 4

b. f(x) = 4 ( x^2 - 1)^2

c. f(x) = 3(2-x^2)^3

d. g(t) = -4 / (t+2)^2  x

2.  Find the third derivative of f(x) = x^4 - 2 x^3

3.  Find the given value:

a.  f '' ( -sqrt(50) if f(x) = 9 - x^2

b.  f ''' ( -2) if f(x) = x^2 ( 3 x^2 + 3 x - 4)

c.  f ''' ( x) if f ''(x) = 20 x^3 - 36 x^2

d.  f '''' (x) if f '''(x) = 2 sqrt(x-1)  x

4.  Solve the equation f '' ( x) = 0

a.  f(x) = x^3 - 9 x^2 + 27 x - 27

b.  f(x) = (x + 2) ( x - 2) ( x + 3) ( x - 3)

c.  f(x) = x / (x^2 + 3)

5.  A brick falls 1250 feet to the sidewalk below, accelerating downward at 32 feet / second^2. 

Write its position function.

Write its velocity and acceleration functions.

How long does it take to reach the sidewalk, and how fast is it moving when it gets there? x

6.  On the graph below, one function is f, another is f ' and the third is f ''.  Which is which, and why?

Assignment 20

1.  Find dy/dx for each of the following, using implicit differentiation:

a.  4 x^2 y - 3 / y = 0

b.  x^2 y^2 - 4 y = 1

c.  (2 y - x) / (y^2 - 3) = 5

d.  (x y - y^2) / (y - x) = 1

2.  Find dy/dx by implicit differentiation, verify that the given point is on the graph of the function, and evaluate the derivative at that point:

a. x^2 + y^2 = 49 at (0, 7)

b.  x^2 - y^3 = 3 at (2, 1)  x

c.  x^2 y + y^2 x = -2 at (2, -1)

d.  x^(1/2) + y^(1/2) = 9 at (16, 25)

e.  sqrt(xy) = x - 2 y at (4, 1)

3.  Graph the equation, and find the slope of each graph at the given point:

a. 4 x^2 + 9 y^2 = 36 at (sqrt(5), 4/3)

b.  x^2 - y^3 = 0 at (-1, 1)

4.  Find dy/dx at the given point.  Then solve the equation explicitly for y, find the derivative using the rules of differentiation, and show that your results are equivalent:

a.  x^2 + y^2 = 25 at (-4, 3)

b.  4 y^2 - x^2 = 7 at (3, 2)

5.  Find the equation of the tangent line at the given point.  It is recommended that you then graph the function and the tangent line, using a graphing utility.  This is a rare situation in which a graphing utility is entirely appropriate, since there is generally no easy way to graph the solution curves of equations.

a.  4 x y + x^2 = 5 at (1, 1) and (5, -1)

b.  y^2 = x^3 / (4 - x) at (2, 2) and (2, -2)

6.  Find the rate of change of x with respect to p for the function p = sqrt((500 - x) / (2x) ), 0 < x <= 500.

Assignment 21

Most students find the topic of Related Rates to be one of the most challenging in the course.  An optional q_a_ has been developed and posted on your Assignments Page, under Assignment 21.

Problems:

1.  For the equation x^2 + y^2 = 25:  x

• find dy/dt, given that x = 3, y = 4 and dx/dt = 8
• find dy/dt, given that x = 4, y = 3 an dy/dt = -2.

2.  The radius of a sphere is changing at 2 inches per minute.  At what rate is the volume changing when r = 6 inches, and when r = 24 inches?

3.  The radius of a right circular cone is increasing at 5 inches per minute.  The height of the cone is 4 times its radius.  At what rate is the volume changing when r = 8 inches, and when r = 32 inches?

4.  A 20-foot ladder rests against a vertical wall.  The bottom of the ladder is pulled along the ground, away from the wall, at 3 ft / sec.  As the base of the ladder moves away from the wall, of course the top of the ladder moves down the wall.  How fast is the top descending along the wall when the base is 5 ft from the wall?  How fast when the base is 12 ft from the wall?  (Hint: how are the distance of the base from the wall and the height of the top of the ladder along the wall related?)

5.  An oil slick is growing due to an ongoing spill.  It is 300 meters in diameter and .02 meters thick.  Its radius is expanding at .15 meters / minute.  At what rate, in cubic meters per minute, is oil therefore flowing into the spill?

Assignment 22

1.  Evaluate the derivative of the given function at the given point:

a.  f(x) = x + 32 / x^2 at (4, 6)

b.  f(x) = (x + 2)^(2/3) at (-2, 0)

c.  f(x) = -3x sqrt(x+1) at (-2/3, 2 sqrt(3)/3)  x

2.  Using the derivative, find the intervals on which each function is increasing or decreasing:

a.  f(x) = x^3/4 - 3 x

b.  f(x) = x^4 - 2 x^2

c.  f(x) = x^2 / (x+1)

3.  Using the derivative, find the critical numbers for each function, and the intervals on which the function is increasing and decreasing, and describe the graph of the function:

a.  g(x) = (x + 2)^2

b.  y = x^3 - 6 x^2

c.  f(x) = 3x^3 + 12 x^2 + 15 x

d.  y = x^3 - 3x + 2

e.  f(x) = x / (x+1)  x

4.  The profit made by selling x items is modeled by

P = 2.4 x - x^2 / 25 000 - 3500, 0 <= x <=50 000

• On what intervals is the profit P increasing and on what intervals is it decreasing?
• What selling price do you think maximizes the profit?

Assignment 23

1.  Find all relative extrema of the given functions, using derivatives:

a.  f(x) = x^2 - 6 x

b.  f(x) = -4 x^2 + 4 x + 1

c.  g(x) = - (x + 4)^2

d.  h(x) = x^4 - 32 x + 4               x

2.  Find the absolute extrema of each given function on the given interval, using derivatives and the methods of the section:

a.  f(x) = 2 ( 3 - x) on [-1, 2]

b.  g(x) = x^2 + 2 x - 4 on [-1, 1]

c.  p(t) = 1 / (c - t) on [0, 2].

d.  h(x) = 4 ( 1 + 1/x + 1/x^2) on [-4, 5].

e.  s(q) = 6 / (q + 2) on [0, infinity)

3.  Find the maximum value of | f(x) |, where f(x) = x^3 ( 3x^2 - 10) on [0, 1].

4.  The demand x for a product is inversely proportional to the cube of the price p, as long as p is at least $1.  When the price is $10 each, the demand is 8 items.  The cost of manufacture is $100 setup cost plus $4 per unit.  What price yields the maximum profit?

Assignment 24

1.  Using derivatives and the methods of the section, find the intervals on which each graph is concave upward and those on which it is concave downward.   Your results should be consistent with the graphs shown for the functions.

y = -x^3 + 3 x^2 - 2

y = (x^2 + 4) / (x - 4)^2

y = x^5 + 5 x^4 - 40 x^2                             

x

2.  Find all relative extreme of each function, using the second-derivative test where it applies.

a.  f(x) = x^3 - 5 x^2 + 7 x

b.  f(x) = x^(2/3) - 5

c.  f(x) = x / (x^2 - 1)

3.  Give the signs of f ' (x) and f '' (x) on the interval (0, 2).              x

4.  Find the point(s) of inflection for the given functions:

a.  f(x) = x^3 - 9 x^2 + 24 x - 18

b.  g(x) = x^4 - 18 x^2 + 5

c.  f(t) = (1 - t) * t - 4) ( t^2 - 4)

5.  The graph below is of f ' (x).  Determine the intervals on which f ' is positive, negative, increasing and decreasing.  (instr. reference: obvious neg cubic leading coeff 1/3 zeros at origin and x=2)

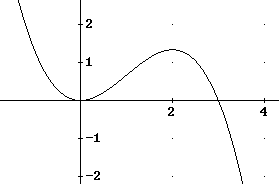
6.  The cost of producing x units is C(x) = 0.002 x^3 + 20 x + 500.  What production level minimizes the average cost per unit?

Assignment 25

1.  Find two positive numbers with the given properties:

a.  The sum of the first and twice the second is 36 and the product is a maximum.

b.  The product is 192 and the sum of the first plus three times the second is a minimum.   x

c.  Their difference is 50 and their product is a minimum.

2.  Find the length and width of a rectangle with the given properties:

a.  perimeter 100 meters, maximum area

b.  area A

3.  Three rectangular solids have the following dimensions:

• 3 x 3 x 11
• 5 x 5 x 5
• 6 x 6 x 3.25

Do the following:

• Verify that all three have the same surface area.
• Find the volume of each.
• Find the dimensions of a rectangular solid with square base, area 150 square inches, and the maximum possible volume.

4.  A 2 ft x 3 ft rectangle is to be made into an open box by cutting a square from each corner and folding up the sides.  What is the volume of the largest possible box?

5.  If a farmer plants 80 apple trees in a field, she can expect a yield of 400 apples per tree.  For each additional tree planted the yield per tree decreases by 4 apples.  How many trees should be planted to maximize the yield?

6.  A rectangle is bounded by the x axis and the semicircle y = sqrt( 36 - x^2).  What should be its length and width, in order to maximize its area?

7.  You want to design a room with a perimeter of 200 meters.  The shape of the room is to be rectangle with semicircles on both ends.  What should be its dimensions?

Assignment 26

1.  If R = 400 x - x^2, find the number of units x that produces the maximum revenue R.

2.  If C = .001 x^3 + 5 x + 250 is the cost of producing x units, find the number of units x which minimizes the average cost per unit.

3.  If the cost function is C = 35 x + 500 and the demand function is p = 50 - 0.1 sqrt(x), find the price per unit p that maximized the profit function P.   x

4.  If the demand function is p = 100 - 0.5 x^2, with total cost C = 40 x + 37.5, what price yields maximum profit, and what is the corresponding average cost per unit?

5.  A bank can invest deposited money at 12% simple interest.  Assuming that the amount of money deposited is proportional to the square of the interest rate paid by the bank to its depositors, what interest rate will maximize its profit?  (hint to get started:  find the bank's profit if it bank pays 0% interest to its depositors, if it pays 6%, and if it pays 12%; then ask what its profit is if interest is paid at rate r)  x

6.  Average elasticity of demand is defined as follows:

• average elasticity is the percent change in quantity demanded divided by percent change in price.

If a 5% decrease in price is associated with a 3% increase in demand, what is the average elasticity of demand?

If a 2% decrease in price is associated with a 5% increase in demand, what is the average elasticity of demand?

7.  If the demand function is p = 400 - 3 x, then when demand is x = 20:

• If x changes by 5% then by what % does p change?
• What therefore is the average price elasticity of demand on this interval?
• What is the instantaneous price elasticity of demand?

8.  For each function find the elasticity of demand (p / x) / (dp/dx):

a.  p = 5 - .03 x, x = 100

b. p = 100 / x^2 + 2

9.  For demand function p = 20 - .02 x:

• Find the value of x for which price elasticity of demand it equal to 1.
• Find the revenue function and use it to find the maximum total revenue.
• Explain why your results make sense.

Assignment 27

1.   Find the vertical and horizontal asymptotes of the following functions.  Write each asymptote as the equation of a line, and explain the reasons for the asymptote:

a.  f(x) = (x^2 - 2) / (x^2 - x - 2)

b.  f(x) = (-4x) / (x^2 + 4)

c.  f(x) = (x^2 + 1) / (x^3 - 8)

2.  Find the limits, and explain the reasoning required to find each:

a.  limit{x -> 2-} (1 / (x + 2)

b.  limit{x -> 3+} (x - 4) / (x - 3)

c.  limit {x -> 4} x^2 / (x^2 + 16)

d. limit { x -> 0-} (1 + 1/x)

e. limit { x -> infinity} (  (5 x^3 + 1) / (10x^3 - 3x^2 + 7)   )                      x

f. limit {x -> -infinity} 5 x^2 / (x + 3)

g. limit { x -> -infinity} (2x / (x - 1) + 3x / (x + 1) )

3.  Evaluate each of the following for x = 10^0, 10^1, 10^2, 10^3, 10^4, 10^5 and 10^6.  Use your results to conjecture the limit of the function as x -> infinity.

a.  f(x) = (x + 1) / (x sqrt(x))

b. f(x) = 3 x^2 / (0.1 x^2 + 1)

4.  Sketch the graph of each equation.  Explain how you use analysis of intercepts, extrema and asymptotes in the process.

a.  f(x) = x^2 / (x^2 + 9)

b.  f(x) = x / (x^2 - 4)

c.  f(x) = 2x / (1 - x)

d.  f(x) = (x - 2) / (x^2 - 4 x + 3)    x

e.  f(x) = (2 x^2 - 6) / (x-1)^2

5.  The population of a certain animal introduced into the ecosystem of an island is modeled by

• N = 10 ( 3 + 4 t) / (1 + 0.1 t),

where N is the number of animals and t the time in years since the animal was introduced.

• What is the population after 4, 8, 16 and 32 years?
• What do you think is the limiting number of animals, as time progresses?

Assignment 28

1.  Sketch a graph of each of the following functions, showing all intercepts, relative extrema, points of inflection and asymptotes, and state the domain of the function.  Document your analysis, employing the methods of the course.  Choose your scale appropriately.

a.  y = x^3 - 4 x^2 + 6

b.  y = x^3 + 3 x^2 + 3 x + 2

c.  y = 3 x^4 + 4 x^3

d.  y = -x^3 + 3 x^2 + 9 x - 2                             x

e.  y = x^4 - 4 x^3 + 16 x

f.  y = (x - 1)^5

g.  (x^2 + 1) / (x^2 - 1)                                 x

h.  y = (x - 3) / x

k.  y = x^4 / (x^4 - 1)

2.  Each of the graphs below represents a polynomial of form a x^3 + b x^3 + c x + d. 

• For each graph find possible values of a, b, c and d which will result in a graph of the same overall shape.

3.  Use the information accompanying each graph to sketch the graph of f:

a.  The graph below represents f '

b.  The graph below represents f ''

c.  The graph below represents f '

d.  The graph below represents f ''

4.  Sketch a graph of a function with the following characteristics:

• f(-2) = 0
• f(4) = 0
• f ' (2) is undefined
• f ' (x) < 0 for -infinity < x < 2
• f ' (x) > 0 for 2 < x < infinity
• f '' (x) < 0 at all values of x for which x is defined
• limit { x -> -infinity} f(x) = -3

Assignment 29

1.  Find the differential dy for each of the following:

a.  y = (4 x - 1) ^ 3

b.  y = (6 x^2)^(1/3)                            x

c.  y = (1 - 2 x^2)^4

2.  Let x = 1 and `dx = .01.  Find `dy

a.  f(x) = 5 x^2 - 1

b.  f(x) = 4 / x^(1/3)

3.  Compare dy and `dy for each of the following:

a.  y = x^4 + 1, x = -1, `dx = dx = 0.01

b.  y = 1 - 2x^2, x = 0, `dx = dx = -0.1.                             x

4.  Complete the table for each function:

a.  y = x^5

dx = `dx	dy	`dy	`dy - dy	dy / `dy
1.000
.5000
.300
.010
.001

b.  y = 1 / x^2

dx = `dx	dy	`dy	`dy - dy	dy / `dy
1.000
.5000
.300
.010
.001

c.  y = sqrt(x)

dx = `dx	dy	`dy	`dy - dy	dy / `dy
1.000
.5000
.300
.010
.001

4.  Find an equation of the tangent line at the given point.  Compare the function and tangent line values for x = -0.01

a.  f(x) = 3 x^2 - 1 at (2, 11)

b.  f(x) =  x  / (x^2 + 1) at (0, 0).

5.  Using differentials find the approximate change in the given function corresponding to an increase of 1 unit in sales, and explain the meaning of your result

a.  approximate the change in cost if C = 0.05 x^2 + 4 x + 10 and x = 12

b.  approximate the change in revenue if R = 30 x - 1.5 x^2 and x = 75

c.  approximate the change in price if  P = -x^2 + 60 x - 100 and x = 25.

6.  A circle has radius 10 inches.  The possible error in measurement is 1/8 inch.  Using differentials approximate the possible error and the relative error in the calculated value of the circle's area..

7.  The concentration of a drug t hours after injection is C = 3 t / (27 + t^3).  Using differentials approximate the change in drug concentration between t = 1 and t = 1.5.                            x