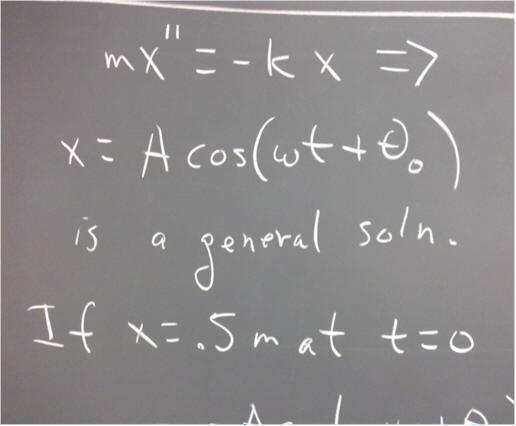110119 Differential Equations

We address the questions posed in qa_01.

Part I:  The equation m x '' = - k x

`q001.  Show whether each of the following functions all satisfy the equation m x '' = -k x:

• y = cos(x)
• y = sin( sqrt( k / m) * x)
• y = 3 cos( sqrt( k / m) * x ) + 5 sin (sqrt(k / m) x)
• y = B sin(sqrt(k / m) * x) + C cos( sqrt( k / m) * x + 3)

****

#$&*

`q002.  An incorrect integration of the equation x ' = x + t is yields x = x^2 / 2 + t^2 / 2 + c.  After all the integral of x is x^2 / 2 and the integral of t is t^2 / 2 and both integrals would have constants which can be combined into the single constant c. 

Show that this function does not satisfy the equation.

Explain what is wrong with the reasoning given above.

****

#$&*

`q003.  The general solution to the equation m x '' = - k x is of the form x = A cos(omega * t + theta_0), where theta_0 is a constant.

What therefore is the general solution to the equation 5 x'' = - 2000 x?

****

#$&*

`q004.  In the preceding equation we found the general solution to the equation 5 x'' = 2000 x.  Assuming SI units, this solution applies to a simple harmonic oscillator of mass 5 kg, which is subject to a net force F = - 2000 N / m * x.  With these units, sqrt(k / m) has units of sqrt( (N / m) / kg), which reduce to radians / second. 

Evaluate the constants A and theta_0 for each of the following situations:

• The oscillator reaches a maximum displacement of .3 at clock time t = 0.
• The oscillator reaches a maximum displacement of .3 , and at clock time t = 0 its position is x = .15.
• The oscillator has a maximum velocity of 2, and is at its maximum displacement of .3 at clock time t = 0.
• The oscillator has a maximum velocity of 2, which occurs at clock time t = 0.  (Hint:  The velocity of the oscillator is given by the function x ' (t) ).

****

#$&*

`q005.  Describe the motion of the oscillator in each of the situations of the preceding problem.  SI units for position and velocity are respectively meters and meters / second.

****

#$&*

Part II:  Solutions of equations requiring only direct integration.

`q006.  Find the general solution of the equation x ' = 2 t + 4, and find the particular solution of this equation if we know that x ( 0 ) = 3.

****

#$&*

`q007.  Find the general solution of the equation x ' ' = 2 t - .5, and find the particular solution of this equation if we know that x ( 0 ) = 1, while x ' ( 0 ) = 7. 

****

#$&*

`q008.  Use the particular solution from the preceding problem to find x and x ' when t = 3.  Interpret your results if x(t) represents the position of an object at clock time t, assuming SI units.

****

#$&*

`q009.  The equation x '' = -F_frict / m - c / m * x ', where the derivative is understood to be with respect to t, is of at least one of the forms listed below.  Which of the given form(s) are appropriate to the equation?

• x '' = f(x, x')
• x '' = f(t)
• x '' = f(x, t)
• x '' = f(x', t)
• x '' = f(x, x ' t)

****

#$&*

`q010.  If F_frict is zero, then the equation x '' = -F_frict / m - c / m * x ' represents the motion of an object of mass m, on which the net force is - c * x '. 

Explain why the expression for the net force is -c * x '.

Explain what happens to the net force as the object speeds up.

****

#$&*

Explain what happens to the net force as the object speeds up.

`q011.  We continue the preceding problem.

• If w(t) = x '(t), then what is w ' (t)? 
• If x '' = - c / m * x ', then if we let w = x ', what is our equation in terms of the function w?
• What is our solution to the equation?
• Assuming that x(t) is the position function, what does our solution mean in terms of the motion of the object?

****

#$&*

Part III:  Direction fields and approximate solutions

`q012.  Consider the equation x ' = (2 x - .5) / (t + 1).  Suppose that x = .3 when t = .2.

If a solution curve passes through (t, x) = (.2, .3), then what is its slope at that point?

What is the equation of its tangent line at this point?

If we move along the tangent line from this point to the t = .4 point on the line, what will be the x coordinate of our new point?

If a solution curve passes through this new point, then what will be the slope at the this point, and what will be the equation of the new tangent line?

If we move along the new tangent line from this point to the t = .5 point, what will be the x coordinate of our new point?

Is is possible that both points lie on the same solution curve?  If not, does each tangent line lie above or below the solution curve, and how much error do you estimate in the t = .4 and t = .5 values you found? 

****

#$&*

`q013.   Consider once more the equation x ' = (2 x - .5) / (t + 1). 

Note on notation:

The points on the grid

(0, 0), (0, 1/4), (0, 1/2), (0, 3/4), (0, 1)

(1/4, 0), (1/4, 1/4), (1/4, 1/2), (1/4, 3/4), (1/4, 1)

(1/2, 0), (1/2, 1/4), (1/2, 1/2), (1/2, 3/4), (1/2, 1)

(3/4, 0), (3/4, 1/4), (3/4, 1/2), (3/4, 3/4), (3/4, 1)

(1, 0), (1, 1/4), (1, 1/2), (1, 3/4), (1, 1)

can be specified succinctly in set notation as

{ (t, x) | t = 0, 1/4, ..., 1, x = 0, 1/4, ..., 1}.

Find x ' at every point of this grid and sketch the corresponding direction field.

Sketch the curve which passes through the point (t, x) = (.2, .3).

Sketch the curve which passes through the point (t, x) = (.5, .7).

****

#$&*

`q014.   We're not yet done with the equation x ' = (2 x - .5) / (t + 1). 

x ' is the derivative of the x(t) function with respect to t, so this equation can be written as

dx / dt = (2 x + .5) * (t + .4).

Now, dx and dt are not algebraic quantities, so we can't multiply or divide both sides by dt or by dx.  However let's pretend that they are algebraic quantites, and that we can.  Note, however, that dx is a single quantity, as is dt, and we can't divide the d's.

• Rearrange the equation so that expressions involving x are all on the left-hand side and expressions involving t all on the right-hand side.
• Put an integral sign in front of both sides.
• Do the integrals.  Remember that an integration constant is involved.
• Solve the resulting equation for x to obtain your general solution.
• Evaluate the integration constant assuming that x(.2) = .3.
• Write out the resulting particular solution.
• Sketch the graph of this function for 0 <= t <= 1.

****

#$&*

`q015.  OK, we might never be done with this equation.  Again, x ' = (2 x - .5) / (t + 1)

• Along what line or curve is x ' = 1?
• Along what line or curve is x ' = 0?
• Along what line or curve is x ' = 2?
• Along what line or curve is x ' = -1?
• Sketch these three lines for 0 <= t <= 1. 
• Along each of these lines x ' is constant.  Along each sketch 'slope segments' with slopes equal to the corresponding value of x '.
• How consistent is your sketch with your previous sketch of the direction field?
• Sketch a solution curve through the point (.2, .25).

****

#$&*