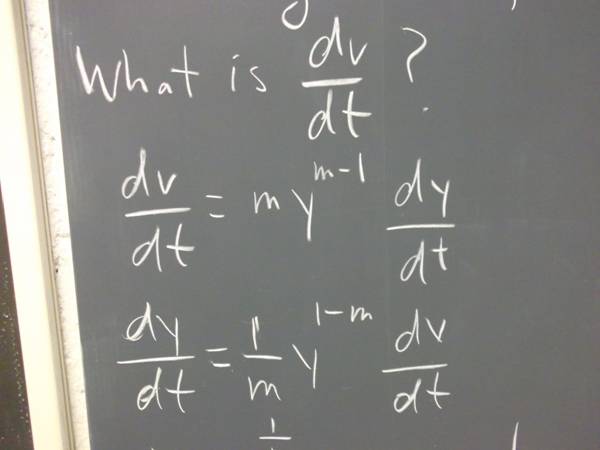110216 differential equations
`q001. Consider the equation
y ' = 3 y^2 * sqrt(t)
This is a separable equation and can be solved. However a very similar equation could be written down which is not solvable. So let's pretend for the moment that this one isn't either.
Suppose we want to calculate an approximate solution curve for which y(1) = .5. Our solution curve will therefore pass through the point (1, .5).
For reference, plot a direction field for this equation on the interval 1 <= t <= 1.2, .5 <= y <= .7.
Now construct an approximate solution by answering the following questions:
What is y ' at the point (1, .5)?
****
#$&*
If we follow this slope as we move .1 unit to the right, in the y vs. t plane, ending up at a new point, what will be our rise?
****
#$&*
What will then be the coordinates of our new point?
****
#$&*
What is y ' at this new point?
****
#$&*
If we follow this slope as we move .1 unit to the right, in the y vs. t plane, ending up at a new point, what will be our rise?
****
#$&*
What will then be the coordinates of our new point?
****
#$&*
We have found two new points by this method. It should be clear that we could continue the process to find as many more new points as we might wish.
****
#$&*
Plot these points on your sketch of the direction field. Do they make sense in the context of that field?
****
#$&*
The new points lie close to, but not exactly on, the solution curve through (1, .5).
****
#$&*
Why do we expect the points to lie close to the solution curve?
****
#$&*
Why don't we expect them to lie exactly on the solution curve?
****
#$&*
Do our points lie above or below the solution curve? Explain how you know.
****
#$&*
`q002. Solve the equation
y ' = 3 y^2 * sqrt(t)
for the initial condition y(1) = .5.
****
#$&*
Evaluate your solution for t = 1.1 and t = 1.2, and plot the resulting two points on your graph of the direction field.
****
#$&*
How close was the first new point obtained in the preceding problem to the actual solution?
****
#$&*
How close was the second new point obtained in the preceding problem to the actual solution?
****
#$&*
`q003. We could get the t = 1.1 approximation by using the same process, with two intervals, each of .05.
What is your approximation to the y value for t = 1.05, based on the slope at (1, .5)?
****
#$&*
What is your approximation to the y value for t = 1.10, based on the slope at the point you just found?
****
#$&*
How far from the known solution is your new t = 1.10 approximation?
****
#$&*
Originally we got to t = 1.1 by a single step. We have now used two steps to get a new approximation.
****
#$&*
By what factor did our approximation error change?
****
#$&*
Did doubling the number of steps reduce the error in the approximation by a factor of two, less than two or more than two?
****
#$&*
Why did the approximation error change as it did?
****
#$&*
`q004. BB data: Shot at the same trajectory the BB follows a path similar to that of a good sand wedge shot in golf, but I believe it starts out with greater velocity and loses speed more quickly. In the sunlight against a blue sky you can track the thing for just about its entire flight. Pretty neat. Shot at the Moon, without correcting for gravity, and didn't really miss it by all that much. Don't want to steal NASA's thunder to I'll leave it at that. Shot into water at a low enough trajectory it will skip without losing too much speed. Shot at a nearly vertical trajectory the water stops it within a few centimeters. All this appears to be consistent with the gun's rating of 0.3 Joules and the BB's .12 gram mass (which is in turn consistent with the 250 ft/sec muzzle velocity). At that speed the BB should climb for about 1000 feet, if shot in a vacuum, which is what leads me to believe it's losing velocity.
How could differential equations be used to provide models for this discussion?
****
#$&*
What tests are suggested by the solutions of those equations?
****
#$&*





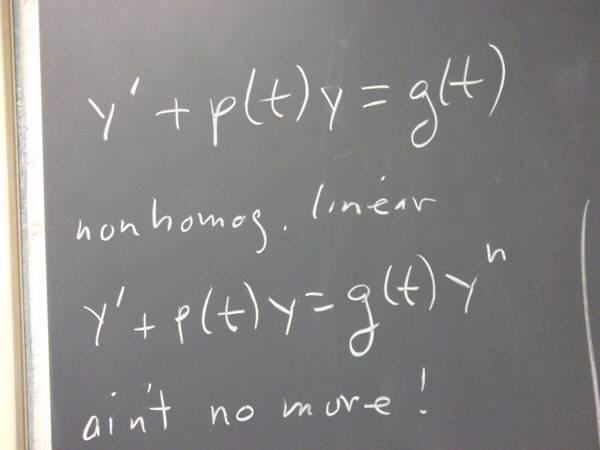


-1/y=2 t^(3/2) + c
y = -1 / (2 t^(3/2) + c)
-1 / (2 + c) = 1/2 so c = -4
y=-1 / (2 t^(3/2) - 4)