110302 Differential Equations

`q001.  Find a solution to the equation

y '' + 3 y'  - 4 y = 2 e^(5 t).

Hint:  If you're going to get a multiple of e^(5 t) out of a combination of derivatives of y, then y had better be some multiple of e^(5 t). 

****

#$&*

You could easily solve the equation y '' + 3 y ' - 4 y = 0.  You would get the fundamental set { e^t, e^(-4 t) }.

Show that if you add a linear combination c_1 e^t + c_2 e^(-4 t) to the solution you have found, you still get a solution to the original equation y '' + 3 y'  - 4 y = 2 e^(5 t).

****

#$&*

`q002.  Find a solution to the equation

y '' + 3 y ' - 4 y = t^2.

Show first that if you have a nonzero multiple of t^3 in your trial solution, and no higher powers of t, then y '' + 3 y ' - 4 y will contain a nonzero multiple of t^3.  Conclude that any trial solution had better not contain t^3.

****

#$&*

Show that if your trial solution consists of a nonzero multiple of t^2, then y '' + 3 y ' - 4 y will include a nonzero multiple of t^2, but it will also contain a nonzero multiple of t and a nonzero constant.

****

#$&*

Show that if your trial solution is of the form y = a t^2 + b t + c, then for the right values of a, b and c the expression y '' + 3 y ' - 4 y could contain a nonzero multiple of t^2, with the coefficient of t and the constant term both equal to zero.

****

#$&*

`q003.  Find a solution to the equation

y '' + 3 y ' - 4 y = 3 cos(2 t).

Hint:  The only functions whose solutions are multiples of cos(2 t) are sin(2 t) and cos(2 t), so your trial solution should be a linear combination of those functions.

****

#$&*

`q004.  The method illustrated by the above works fine when the right-hand side is a certain type of combination of polynomials, sines, cosines and exponentials.  However it doesn't otherwise work very well.

Consider the equation

y '' + 3 y ' - 4 y = t ln(t).

We aren't likely to figure out the form of a solution whose combined first and second derivatives, etc., is equal to t ln(t).

So we try a solution of the form y = u_1 e^t + u_2 e^(-4 t), sort of a linear combination of the functions in the fundamental set, except that u_1 and u_2 are not constants but functions of t.  We want to try to figure out what those functions are.

Substitute this function into the equation and see what you get.

****

#$&*

`q005.  Repeat the preceding exercise, but this time assume that y_1 u_1 ' + y_2 u_2 ' = 0.  This will greatly simplify the expression for y ', which was u_1 ' y_1 + u_1 y_1 ' + u_2 ' y_2 + u_2 y_2 '.  In turn, this will simplify the expression for y ''.

With the above modification, what do you get when you substitute into the equation?

****

#$&*

`q006.  In the above, the constants you get from e^t and e^(-4 t) actually confuse the issue.

Just let y = u_1 y_1 + u_2 y_2.

You get

y ' = u_1 ' y_1 + u_1 y_1 ' + u_2 ' y_2 + u_2 y_2 '

but with u_1 ' y_1 + u^2 ' y_2 = 0 this is just

y ' = u_1 y_1 ' + u^2 y^2 ' ,

so

y_2 '' = u_1 ' y_1 ' + u_1 y_1 '' + u_2' y_2 ' + u_2 y_2 ''.

Plug these expressions into the equation and see what you get.

****

#$&*

Collect all the terms which are multiples of u_1, and write them with u_1 factored out.

Collect all the terms which are multiples of u_2, and write them with u_2 factored out.

Two terms will remain.

What is your equation, in this form?

****

#$&*

The u_1 and u_2 terms should be

(y_1 '' + 3 y_1 ' - 4 y_1) u_1

and

(y_2 '' + 3 y_2 ' - 4 y_2) u_2

Since y_1 and y_2 are solutions of the equation y '' + 3 y ' - 4 y = 0, these terms will be zero.

What is left of your equation after you remove these terms?

****

#$&*

This equation, along with the equation y_1 u_1 ' + y_2 u_2 ' = 0 (assumed earlier), give us two simultaneous equations in the unknowns u_1 and u_2.  What are those equations?

****

#$&*

Write these equations as matrix equations.  Do you recognize the matrix on the left-hand side?

****

#$&*

What is the determinant of that matrix?

****

#$&*

***
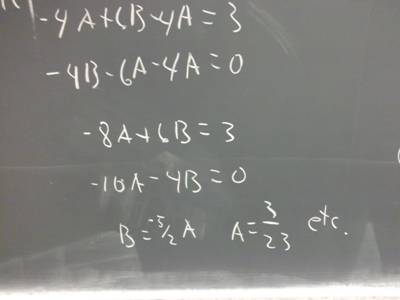
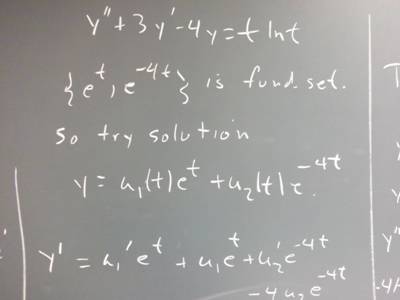