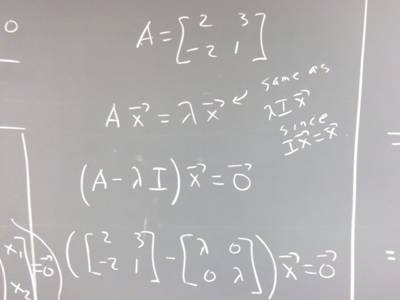110321 Differential Equations
1. Write out the system of two equations corresponding to each of the following matrix equations:
[ 2, 3 ; -2, 1 ] * [y_1, y_2] ` = [y_1' , y_2' ]`
****
#$&*
[ t, sin(t); 1/t, t^2 ] * [y_1, y_2] ` = [y_1' , y_2' ]`
****
#$&*
[ 2, 3 ; -2, 1 ] * [y_1, y_2] ` + [1, t] ` = [y_1' , y_2' ]`
****
#$&*
2. Write each of the systems in matrix form:
system 1:
y_1 ' = 3 y_1 + 2 y_2
y_2 ' = 2 y_1 - 4 y_2
****
#$&*
system 2:
y_1 ' = 2 t y_1 - cos(t) y_2 + 4
y_2 ' = 3 y_1 - 4 / t y_2 + 1
****
#$&*
3. Find the derivative of the matrix
[ t, sin(t); 1/t, t^2 ]
****
#$&*
Find an antiderivative of this same matrix.
****
#$&*
4. Let A = [ t, sin(t); 1/t, t^2 ] and B = [ cos(t), t; sqrt(t), 1/t ].
Show that (A B) ' = A ' B + A B '.
****
#$&*
5. Find the value(s) lambda for which A x = lambda x, where A is the matrix
[ 2, 3 ; -2, 1 ]
and x is an unspecified vector.
****
#$&*
6. For each value of lambda found in the preceding, find a vector x for which the equation A x = lambda x is true.
****
#$&*
7. Let lambda_1 and lambda_2 be the solutions you found for #5, and x_1, x_2 the corresponding vectors you found in #6.
Show that y = [y_1, y_2] ` = e^(lambda_1 * t) * x_1 is a solution to the equation
[ 2, 3 ; -2, 1 ] [y_1, y_2] ` = [y_1 ' , y_2 ' ] `
****
#$&*
Show the analogous result for e^(lambda_2 * t) * x_2.
****
#$&*
Show furthermore that
c_1 e^(lambda_1 * t) * x_1 + c_2 e^(lambda_2 * t) * x_2
is a solution to the equation.
****
#$&*