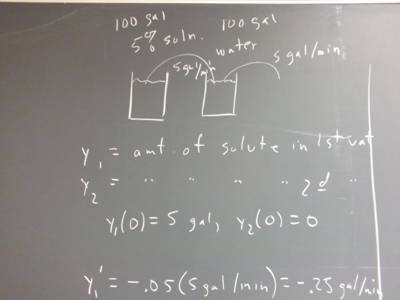110328 Differential Equations
`q001. Suppose there are 10 000 rabbits and 200 foxes in a certain area, while in another equivalent area there are 12 000 rabbits but only 10 foxes. In which area would you expect more of the rabbits to encounter foxes and why?
****
#$&*
In which of the systems would you expect more rabbits to encounter foxes on a
given day?
****
#$&*
In which system would you expect the average fox to catch more rabbits?
****
#$&*
In which system would you expect the rabbit population to grow more rapidly?
****
#$&*
What would an increased number of rabbits do to the nourishment of the foxes?
****
#$&*
How would you expect this to affect the population of foxes?
****
#$&*
What effect would an increase in the population of foxes have on the population
of rabbits?
****
#$&*
`q002. Suppose again that on a certain day we have 10 000 rabbits and 200 foxes
in an area.
Let's assume that the number of rabbit-fox encounters per day is proportional to
the number of rabbits multiplied the the number of foxes, divided by 150, and
that in 1% of these encounters it ends up bad for the rabbit, good for the fox.
How many rabbits will therefore get eaten on this particular day?
****
#$&*
Let's furthermore assume that the number of daily rabbit births is 2% of the
total rabbit population every day, that in the absence of rabbits 1.5% of the
foxes will die every day, and that every 50 rabbits eaten will result in a new
fox. Assume that rabbits never die, or if they do the death rate is absorbed
into the birth rate.
On this particular day, does the population of rabbits increase or decrease, and
by how much?
****
#$&*
Does the number of foxes increase or decrease, and by how much?
****
#$&*
Is the percent increase in the rabbit population greater or less than the
percent increase in the fox population?
****
#$&*
`q003. Continuing the preceding, what will be the changes in rabbit and fox
populations on the next day?
****
#$&*
What do you expect will be the population trend over the next 100 days?
****
#$&*
`q004. Continuing the preceding, if R is the rabbit population, F the fox
population, with dR/dt and dF/dt indicating the derivatives of R and F with
respect to clock time (clock time in days).
In terms of R, F, and the given percents:
What is the expression for the number of rabbits born per day?
****
#$&*
What is the expression for the number of rabbits eaten per day?
****
#$&*
What is the expression for the number of foxes born each day?
****
#$&*
What is the expression for the number of foxes that die each day?
****
#$&*
What is the expression for dR/dt?
****
#$&*
What is the expression for dF/dt?
****
#$&*
`q005. The preceding should have given you a system of linear differential
equations, relating dR/dt to R and F, and relating dF/dt to R and F.
Solve this system.
****
#$&*
`q006. A full 100-gallon tank contains a 5% solution of a certain solute. Another 100-gallon tank is full of water.
Solution is pumped from the first tank into the second at 5 gallons / minute, with the overflow being discarded. Assume that the solution flowing into the second tank is thoroughly mixed as soon as it enters the tank.
Let y_1 be the amount of solute in the first tank, y_2 the amount in the second. What are the equations for dy_1 / dt and dy_2 dt, in terms of y_1 and y_2?
****
#$&*
The system of equations we get from the above is not particularly interesting.
Let's now assume that the overflow from tank 2 is pumped back into tank 1. What now are the equations for dy_1 and dy_2?
****
#$&*
Solve this system.
`q007. Now solve the system for the condition that 5 gallons per minute are pumped from tank 1 into tank 2, and 3 gallons per minute are pumped from tank 2 back into tank 1, with the remaining 2 gallons per minute discarded from tank 2. Set up and solve this system, and find the concentration in tank 2 at the instant tank 1 becomes empty.
****
#$&*
`q008. For the situation of the preceding, assume that now an additional 2 gallons / minute of pure water is being pumped into tank 1, maintaining it at its 100 gallon capacity. Set up but do not solve this system.
****
#$&*