110406 Differential Equations

1.  The Laplace Transform of a function f(t) is integral( f(t) * e^-(s t) dt, t from 0 to infinity).

Derive the Laplace Transforms of the following functions:

f(t) = e^(k t)

****

#$&*

f(t) = t^3

****

#$&*

f(t) = cos(omega t)

****

#$&*

f(t) = 7

****

#$&*

****

#$&*

2.  Find a formula for the Laplace Transform of f ' (t), in terms of the Laplace Transform of f(t).

****

#$&*

3.  Find a formula for the Laplace Transform of integral(f(u) du, u from 0 to t), in terms of the Laplace Transform of f(t).

****

#$&*

4.  Show that the Laplace Transform of the function h(t) = a * f(t) + b * g(t) is equal to a * L(f(t)) + b * L(g(t)), where L(f(t)) is the Laplace Transform of f(t), etc..  That is, show that the Laplace Transform is a linear operator on the space of functions.

****

#$&*

5.  If the Laplace Transform of a function is 1 / (s - 4), then what is the function?  That is, what is the inverse Laplace Transform of the expression 1 / (s - 4)?

****

#$&*

6.  Consider the mixing problem, where water flows into two full tanks, each of volume V, at rate r, and solution flows out of both at the same rate.  In the problem as posed previously, the solutions in the two pipes connecting the tanks also flow at the same rate. 

How does the system change if the flow in the connecting pipes is cut in half?

****

#$&*

How does this affect the solution of the system?

****

#$&*

The equation at the top is the result of two integrations by parts, starting with integral(e^t sin(omega t) dt).

Below that we begin the integration for the Laplace Transform of e^(k t).

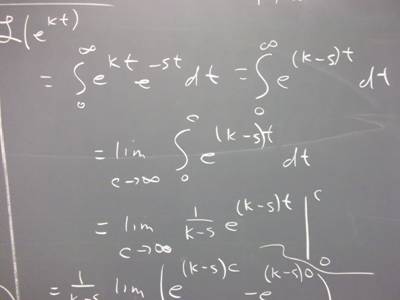
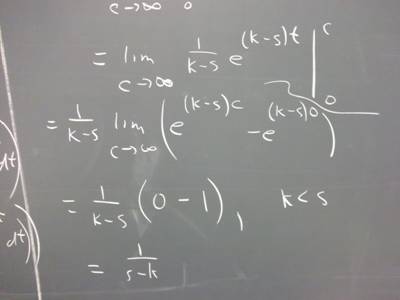
The last expression above approaches zero as t -> infinity, due to the e^(-s t). 

At t = 0 the expression evaluates to -6 / s^4; zero being the lower limit of the integral this gives us a final result of 6 / s^4.

It should be easy to see how the 6 comes from the factors 3 and 2 in the integrations by parts, and how each integration by parts adds a power of s to the denominator.

In general the Laplace Transform of t^n is n ! / s^(n + 1). 

(note that we're being careless about writing the limits 0 and infinity on the integrals)

(the 'miracle' is simply restoration of 0 and infinity to their rightful places, and evaluation of the antiderivative between the limits 0 and infinity.  As we approach infinity the integral approaches zero because of e^-(s t).  At the lower limit t = 0 we have cos(omega t) = 1 and sin(omega t) = 0)