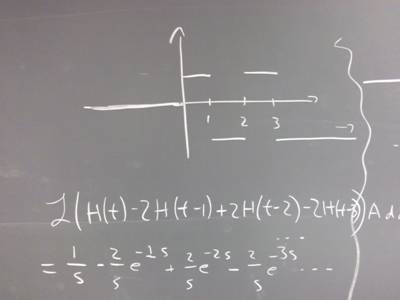110411 Differential Equations

1.  Find solutions of

y ' =  [ 5, 3; -4, -3 ] y

for which y(1) = [2; 0].

****

#$&*

Find the expression for W(t), the Wronskian of the solution.

Show that W(t) = W(1) * e^(integral(2 ds, s from 1 to t)).

****

#$&*

2.  We have seen (and should be able to prove) that the Laplace transform of the derivative function of the function y(t) is given by

L(y ' ) = s * L(y) - y(0)

You should have done the integral to show that

L(e^(alpha t)) = 1 / (s - alpha)

(the integral is just integral( e^(alpha t) * e^(-s t) dt, t from 0 to infinity) ).

We can use these facts to solve the familiar equation

y ' = - k y

Transform the equation and solve for L(y).

****

#$&*

Having found L(y), find the function of which L(y) is the transform.

****

#$&*

3.  The Heaviside function is

H(t) =

0 if t < 0,

1 if t >= 0.

What is the Laplace Transform of H(t)?

****

#$&*

4.  What is the definition of the function H(t - alpha)?

****

#$&*

What is the Laplace Transform of H(t - alpha)?

****

#$&*

5.  Sketch a graph of the following function, and give a description of your graph and the process you used to construct it:

H(t) - 2 H(t - 1) + 2 H(t - 2) - 2 H(t - 3).

****

#$&*

What is the Laplace Transform of this function?

****

#$&*

What does this function have to do with the square waves you have been generating in physics class?

****

#$&*

6.  What is the Laplace Transform of the function y = A cos(omega t + phi)?

****

#$&*

What might this have to do with alternating circuits?

****

#$&*

7.  See if you can figure out the formula for L(y '').  Hint:  Two easy integrations by parts will do it.  Just write down the integral and go to it.

****

#$&*