prior to class 110202
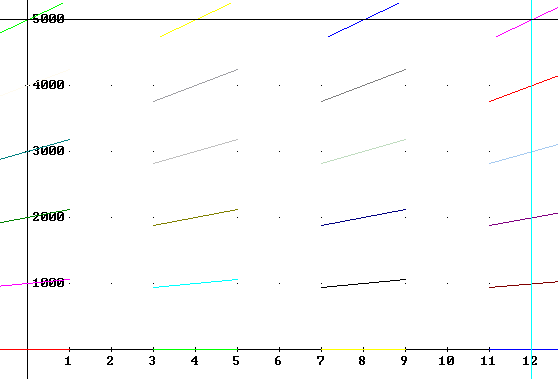
`q001. The direction field shown in the figure below applies to the equation dP/dt = k P, with k = .06.

For P = 2000, what should be the slope of the direction field, according to the equation dP/dt = .06 P?
****
#$&*
Do the slopes here appear to match the slope you just calculated?
****
#$&*
The slope you should have obtained was over 100. The slopes on this direction field all appear to be less than 1. We need to either reconcile this, or discard the direction field of the figure.
Let's first check out a solution to the problem. As you can easily verify, dP/dt = k P gives us general solution P(t) = C e^(k t). To get the solution passing through the P axis at 2000, we apply the initial condition P(0) = 2000. Our particular solution for this initial condition is P(t) = 2000 e^(k t). Our direction field is for k = .06; for P(0) = 2000 our function is therefore P(t) = 2000 e^(.06 t). A graph of this function is consistent with the direction field.
Verify this. Following the trend of the direction field, estimate the likely value of P(3). What is your estimate?
****
#$&*
What do you get if you evaluate P(3)? Is this consistent with your estimate?
****
#$&*
According to the direction field, does the solution curve through (0, 2000) exit the box to the right or through the top?
****
#$&*
Check this out by evaluating P(12). What is your conclusion?
****
#$&*
Reasonable answers to these questions will tend to reinforce our confidence in the direction field.
Consider the direction field line through (8, 4000). Based on the scale of your graph, estimate the rise of that segment. It should be obvious that the run of the segment is 2. What therefore is the slope represented by that segment?
****
#$&*
The slope appears to be less than 1. Explain why that segment actually represents a slope in the hundreds.
****
#$&*
Construct the slope field for the equation dP/dt = .06 P, for the interval 10 000 <= P <= 20 000, 0 <= t <= 12. Scale your slope segments appropriately.
Based on your slope field, at what value of t do you estimate the value of P(t) will double, starting with P = 10 000 at t = 0?
****
`q002. A quantity y is directly proportional to a quantity x if there exists a constant k such that y = k x.
The rate, with respect to time, at which the temperature of an object left to cool in a room at temperature T_room is directly proportional to the difference between the temperature of the object, which we will represent by T(t), and the temperature of the room.
Letting T ' (t) stand for the rate at which the temperature T(t) changes with respect to clock time, write down the proportionality.
****
#$&*
You should have written down a differential equation. That equation is linear. Find its general solution.
****
#$&*
If the object has an initial temperature of 50 Celsius, and its temperature initially changes at -5 Celsius per minute when placed in a room at temperature 20 Celsius, then what is the specific function that models its temperature as a function of time?
****
#$&*
`q003. Consider the equation dy/dt = -.01 y^2.
Explain why we cannot solve this equation using the techniques we have been applying to first-order linear equations.
****
#$&*
We will see why shortly, but for now accept that this equation can be rearranged into the form
dy / y^2 = -.01* dt
and integrate both sides to get a general solution.
****
#$&*
`q004. Consider the equation dy/dt = .01 t y^2. Algebraically rearrange this equation so that dy is a factor of one side, with all other y factors on that side, and dt, along with all other t factors, is on the other.
Integrate both sides of the equation to get a general solution.
****
#$&*
Find the particular solution for which y = 25 when t = 0.
****
#$&*
Show that the function f(t, y) = .01 t y^2 is defined and continuous for all values of y and t.
****
#$&*
Show that there exist values of t for which your solution is neither defined nor continuous.
****
#$&*
While a linear equation of the form y ' + p(t) y = g(t) always has a solution which is defined and continuous, on any interval for which p(t) and g(t) are defined and continuous, this example shows that the same is not necessarily so for an equation of the form y ' + f(t, y) = 0. Explain this statement.
****
#$&*
`q005. The rate, with respect to time, at which the velocity of a spherical object moving through water changes is directly proportional to the square of its velocity.
Write this as a differential equation.
****
#$&*
Solve the equation.
****
#$&*
If the object is initially moving at 30 cm/s and changing velocity at the rate of 1000 cm/s^2, then what function describes its velocity?
****
#$&*
`q006. Recall implicit differentiation. If you need a review of implicit differentiation see the q_a_ document at http://vhcc2.vhcc.edu/dsmith/genInfo/qa_query_etc/cal1/cal1_qa16.htm . If you need a review of the chain rule, see http://vhcc2.vhcc.edu/dsmith/genInfo/qa_query_etc/cal1/cal1_qa12.htm and http://vhcc2.vhcc.edu/dsmith/genInfo/qa_query_etc/cal1/cal1_qa13.htm .
If y is a function of t, then what is the derivative with respect to t of the function H(t, y) = t cos y + 1/y?
****
#$&*
`q007. Verify that the derivative of the function H(t, y) = t^2 sqrt(y) is 2 t sqrt(y) + t^2 / (2 sqrt(y) ) * y '.
****
#$&*
Verify that the equation
2 t sqrt(y) + t^2 / (2 sqrt(y) ) * y ' = 0
is of the form
( H(t, y) ) ' = 0,
where H(t, y) = t^2 sqrt(y) and ' indicates the derivative with respect to t.
****
#$&*
Verify that the equation
( H(t, y) ) ' = 0
is equivalent to the equation
H(t, y) = c,
where c is any constant number.
****
#$&*
For the given function H(t, y) = t^2 sqrt(y), solve the equation
H(t, y) = c
for y as a function of t.
****
#$&*
Show that this function y(t) satisfies the equation
2 t sqrt(y) + t^2 / (2 sqrt(y) ) * y ' = 0.
****
#$&*