Section 2.2

Question:  1.  Solve the following equations with the given initial conditions:

1.  y ' - 2 y = 0, y(1) - 3

Your solution: 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

Self-critique rating:

Question:  2.  t^2 y ' - 9 y = 0, y(1) = 2.

Your solution: 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

Self-critique rating:

Question:  3.  (t^2 + t) y' + (2t + 1) y = 0, y(0) = 1.

Your solution: 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

Self-critique rating:

Question:  4.  y ' + sin(3 t) y = 0, y(0) = 2.

Your solution: 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

Self-critique rating:

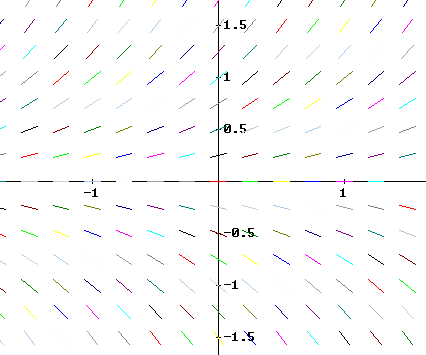
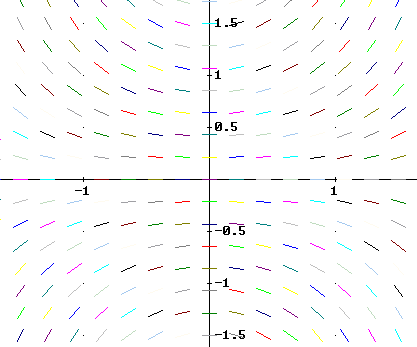
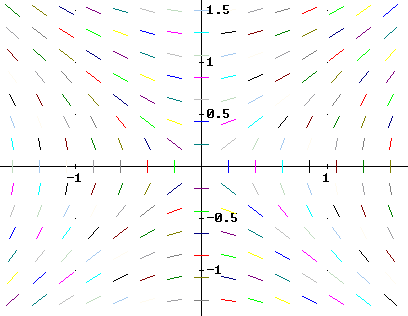
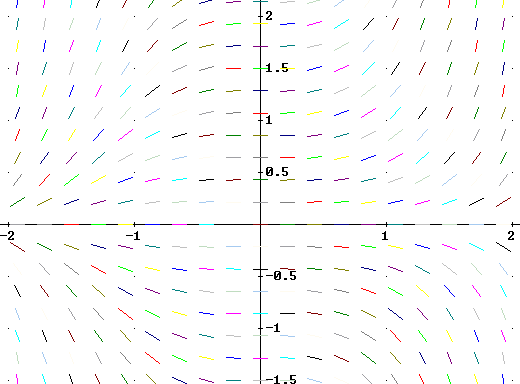
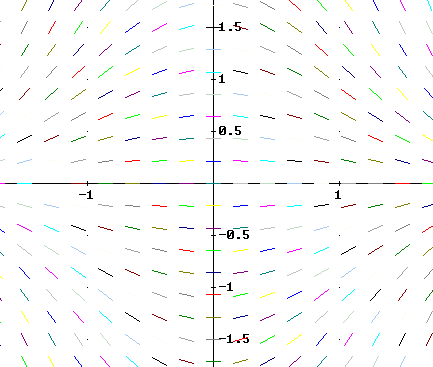
Question: 5.  Match each equation with one of the direction fields shown below, and explain why you chose as you did.

y ' - t^2 y = 0

****

#$&*

y ' - y = 0

****

#$&*

y' - y / t = 0

****

#$&*

y ' - t y = 0

****

#$&*

y ' + t y = 0

****

#$&*

A

B

C

D

E

F

6.  The graph of y ' + b y = 0 passes through the points (1, 2) and (3, 8).  What is the value of b?

Your solution: 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

Self-critique rating:

Question: 

7.  The equation y ' - y = 2 is first-order linear, but is not homogeneous.

If we let w(t) = y(t) + 2, then:

What is w ' ?

****

#$&*

What is y(t) in terms of w(t)?

****

#$&*

What therefore is the equation y ' - y = 2, written in terms of the function w and its derivative w ' ?

****

#$&*

Now solve the equation and check your solution:

Solve this new equation in terms of w.

****

#$&*

Substitute y + 2 for w and get the solution in terms of y.

****

#$&*

Check to be sure this function is indeed a solution to the equation.

****

#$&*

Your solution: 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

Self-critique rating:

Question:  8.  The graph below is a solution of the equation y ' - b y = 0 with initial condition y(0) = y_0.  What are the values of y_0 and b?

Your solution: 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

Self-critique rating: