Query 18 Differential Equations

Question:  A 10 kg mass stretches a spring 30 mm beyond its unloaded position.  The spring is pulled down to a position 70 mm below its unloaded position and released. 

Write and solve the differential equation for its motion.

Your solution: 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

Self-critique rating:

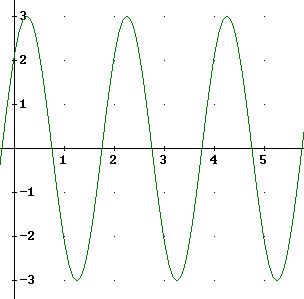
 Question:  The graph below represents position vs. clock time for a mass m oscillating on a spring with force constant k.  The position function is y = R cos(omega t - delta).

Find delta, omega and R.

Give the initial conditions on the y and y '.

Determine the mass and the force constant.

Describe how you would achieve these initial conditions, given the appropriate mass and spring in front of you.

Your solution: 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

Self-critique rating:

Question:  This problem isn't in your text, but is related to the first problem in this set, and to one of the problems that does appear in your text.  Repeating the first problem:

'A 10 kg mass stretches a spring 30 mm beyond its unloaded position.  The spring is pulled down to a position 70 mm below its unloaded position and released. 

Write and solve the differential equation for its motion.'

Suppose that instead of simply releasing it from its 70 mm position, you deliver a sharp blow to get it moving at downward at 40 mm / second. 

What initial conditions apply to this situation?

Apply the initial conditions to the general solution of the differential equation, and give the resulting function.

Your solution: 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

Self-critique rating:

Question:  The 32-pound weight at its equilibrium position in a critically-damped spring-and-dashpot system is given a 4 ft / sec downward initial velocity, and attains a maximum displacement of 6 inches from equilibrium.  What are the values of the drag force constant gamma and the spring constant k?

Your solution: 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

Self-critique rating:

Question:  The motion of a system is governed by the equation m y '' + gamma y ' + k y = 0, with y(0) = 0 and y ' (0) = v_0.

Give the solutions which correspond to the critically damped, overdamped and underdamped cases.

Show that as gamma approaches 2 sqrt(k * m) from above, the solution to the underdamped case approaches the solution to the critically damped case.

Show that as gamma approaches 2 sqrt(k * m) from below, the solution to the overdamped case approaches the solution to the critically damped case.

Your solution: 

Confidence rating:
 

Given Solution: 

Self-critique (if necessary):

Self-critique rating: