026. Modular systems

Question: `q001. There are 7 questions in this assignment.

We defined an operation as follows: x * y (mod 4) = remainder when x * y is divided by 4.

Find 3 * 9 (mod 4); 7 * 12 (mod 4) and 11 * 13 (mod 4).

Your solution:

Confidence Assessment:

Given Solution:

3 * 9 (mod 4) is the remainder when 3 * 9 is divided by 4. Since 3 * 9 = 27 and 27 / 4 leaves remainder 3, we see that 3 * 9 (mod 4) = 3.

7 * 12 (mod 4) is the remainder when 7 * 12 is divided by 4. Since 7 * 12 = 84 and 84 / 4 leaves remainder 0, we see that 7 * 12 (mod 4) = 0.

11 * 13 (mod 4) is the remainder when 11 * 13 is divided by 4. Since 11 * 13 = 143 and 143 / 4 leaves remainder 3,we see that 11 * 13 (mod 4) = 3.

Self-critique (if necessary):

Self-critique Rating:

Question: `q002. Make a table for the x * y mod 4 operation, which we will call '* mod 4', operating on the set {0, 1, 2, 3}.

Determine which of the properties, including commutativity, associative, identity, inverse and closure properties, are properties of this operation.

Your solution:

Confidence Assessment:

Given Solution:

Whatever x is, 0 * x = x * 0 = 0, which when divided by 4 leaves remainder 0.

Whatever x is, 1 * x = x * 1 = x, and if x is in the set {0, 1, 2, 3} we have get remainder x when dividing by 4 (e.g., 4 divides into 0, 1, 2 or 3 zero times, leaving that number as the remainder) and x mod 4 = x. From this we can see that 1 is the identity for this operation.

Multiplying 0, 1, 2, and 3 by 2 we get 0, 2, 4, and 6, which when divided by 4 leave remainders 0, 2, 0 and 2, respectively.

Multiplying 0, 1, 2, and 3 by 2 we get 0, 3, 6, and 9, which when divided by 4 leave remainders 0, 3, 2 and 1, respectively.

The table for this operation is therefore

* mod 4 0 1 2 3

0 0 0 0 0

1 0 1 2 3

2 0 2 0 2

3 0 3 2 1

We note that this operation does contain identity 1, but since neither 0 nor 2 can be combined with any of the elements of the set to give us the identity, the operation on this set does not have the inverse property.

We do see from the symmetry of the table about the main diagonal that it has the commutative property, which we could in any event have concluded from the fact that multiplication is commutative so that the product we get before calculating the remainder is independent of the order of the two numbers.

In a similar matter we can reason that the operation is associative.

The operation is also closed, since the remainder upon dividing by 4 must always be 0, 1, 2 or 3 and hence in the set {0, 1, 2, 3}.

Self-critique (if necessary):

Self-critique Rating:

Question: `q003. Repeat the preceding exercise for the operation x * y mod 5, defined to give the remainder when x * y is divided by 5, on the set {1, 2, 3, 4}. Determine which of the properties are exhibited by this operation.

Your solution:

Confidence Assessment:

Given Solution:

First we might wish to do a couple of example calculations to get familiar with the operation. For example:

2 * 3 mod 5 = 6, which when divided by 5 gives us remainder 1.

3 * 4 mod 5 = 12 which when divided by 5 gives us remainder 2.

2 * 4 mod 5 = 8 which when divided by 5 gives us remainder 3.

The table is

* mod 5 1 2 3 4

1 1 2 3 4

2 2 4 1 3

3 3 1 4 2

4 4 3 2 1

We immediately see that all the results are in the set {1, 2, 3, 4}, so that the operation is closed.

This operation has identity 1, as we can see from the row and the column across from and beneath 1.

We easily see from the table that the identity appears exactly once in each row and in each column, which assures us that the operation has the inverse property. Specifically we see that 1 * 1 mod 5 = 1 so that 1 is its own inverse, that 2 * 3 mod 5 = 1 so that 2 and 3 are inverses, and that 4 * 4 mod 5 = 1, so that 4 is its own inverse.

The associativity and commutativity of the operation follow from the associative and commutative properties of multiplication on real numbers, as discussed in the preceding problem.

Self-critique (if necessary):

Self-critique Rating:

Question: `q004. The equation 3x + 7 = 9 (mod 5) has an integer solution for x = 0, 1, 2, 3 or 4. Which value of x is a solution to this equation?

Your solution:

Confidence Assessment:

Given Solution:

3x + 7 = 9 (mod 4) means that 3x + 7 - 9 = 0 (mod 5) so 3x - 2 = 0 (mod 5). If 3x - 2 = 0 (mod 5) then when we divide 3x - 2 by 5 we should get remainder 0. So we substitute the different possible values for x into the expression 3x - 2 until we get a number of which when divided by 5 gives us remainder 0.

If x = 0 then 3x - 2 = -2, and -2 (mod 5) = 3 (if you don't understand why -2 mod 5 = 3, think of the 5-hour clock in the text; but for now it should be obvious that -2 is not a multiple of 5 so that you cannot get remainder 0 when dividing -2 by 5).

If x = 1 then 3x - 2= 1, and 1 (mod 5) = 1.

If x = 2 then 3x - 2= 4, and 4 (mod 5) = 4.

If x = 3 then 3x - 2= 7, and 7 (mod 5) = 2.

If x = 4 then 3x - 2= 10, and 10 (mod 5) = 0.

Thus x = 4 is a solution to the equation 3x + 7 = 9 (mod 5).

STUDENT QUESTION

What is that 5-hour clock?

INSTRUCTOR RESPONSE

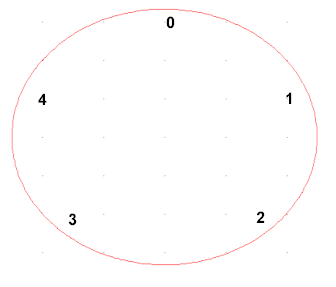
A 5-hour clock is depicted below:

We label the usual 12:00 position 0.  Moving 1 hour at a time in the clockwise direction we encounter hours 1, 2, 3 and 4 before finally returning after 5 hours to the 0 position.

To calculate 3 + 4 on this clock, we start at 0 and move 3 hours, which puts us at position 0.  Then we move 4 more hours, which takes us through positions 4, 0 and 1 before ending up at 2.  Thus, on this clock, 3 + 4  = 2.  It's easy to see how this gives us a picture for the calculation (3 + 4) mod 5, and why the result is the remainder when we divide 3 + 4 by 5.

To calculate 3 * 4 on this clock, we would start at 0 and move 4 hours to position 4, then 4 more hours to position 3, then 4 more hours to position 2.  Thus on this clock 3 * 4  = 2, and this gives us a picture of (3 * 4) mod 5.  It's easy to see that we have moved 3 * 4 = 12 hours, and that where we end up is the remainder when 12 divided by 5.

To divide 3 by 4 on this clock, we observe that for ordinary base-10 division, (3 / 4) * 4 = 3.  So we ask what number multiplied by 4 on this clock will give us 3.  If we start at 0 and move 4 hours around the clock we end up at 4; if we move 4 more hours we end up at 3.  Thus 4 * 2 = 3, and we can therefore say that 2 = 3/4.  That is, 3 divided by 4 is 2.

To solve the equation 3x - 2 = 0:

Next we try different numbers for x:

If x = 1 we get 3 * 1 - 2 = 1.

If x = 2 we get 3 * 2 - 2 = 4.

If x = 3 we get 3 * 3 - 2 = 7.  Since 7 hours on this clock takes us from our starting position at 0 to position 2, we conclude that when x = 3 our result is 3 * 3 - 2 = 2.

If x = 4 we get 3 * 4 - 2 = 10.  Since 10 hours on this clock takes us from our starting position at 0, twice around the clock and back to position 0, we conclude that when x = 4 our result is 3 * 4 - 2 = 0.  So x = 4 is a solution to our equation 3 * x - 2 = 0 (mod 5).

Self-critique (if necessary):

Self-critique Rating:

Question: `q005. You see that x = 4 is a solution to the equation 3x + 7 = 9 (mod 5). One of the numbers x = 5, 6, 7, 8, 9 is also a solution. Which one is it?

Your solution:

Confidence Assessment:

Given Solution:

We recall that 3x + 7 = 9 (mod 5) is equivalent to 3x - 2 = 0 (mod 5). We evaluate 3x - 2 (mod 5) for x = 5, 6, 7, 8 and 9 and we find that the results are 3, 1, 4, 2, and 0. So x = 9 is our next solution.

We might also note that the series of results 3, 1, 4, 2, 0 is the same as the series we got for x = 0, 1, 2, 3, 4. Our results therefore seem to indicate a repeating pattern in which the remainder 0 occurs every fifth number starting with 4. This is in fact what happens, and you might wish to think about why this happens. However, you should in a case remember that this is what happens.

In general when we have an equation of the form A x + B = C (mod n), integer solutions happen at intervals of n. for some values of A, B and C integer solutions can also occur at shorter intervals, but they always do occur at intervals of n.

Self-critique (if necessary):

Self-critique Rating:

Question: `q006. What are the first five positive values of x which solve the equation 3x + 7 = 9 (mod 5) of the preceding problem?

Your solution:

Confidence Assessment:

Given Solution:

We just saw that x = 4 and x = 9 are solutions, and we saw that because we are solving an equation mod 5, the solutions have to occur at intervals of 5. Thus the first five solutions are x = 4, 9, 14, 19 and 24.