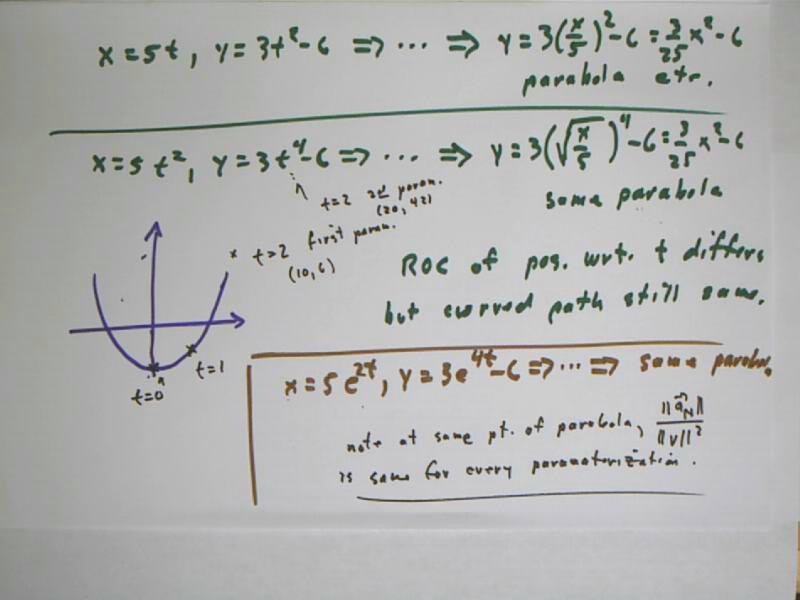Notes are incomplete, but include copies of what was presented in class. Notes will be completed as soon as feasible.
The first figure below is relevant to problems `q001 - `q003 in Section 9.5:
For the parametric equations x = 5 t, y = 3 t^2 - 6 we eliminate t:
x = 5 t, so t = x / 5; substituting this into y = 3 t^2 - 6 we get y = 3 ( x/5)^2 - 6 = 3/25 x^2 - 6.
For the parametric equations x = 5 t^2, y = 3 t^4 - 6 we eliminate t:
x = 5 t^2, so t = +-sqrt(x / 5); substituting this into y = 3 t^4 - 6 we get y = 3 ( +- sqrt(x/5) )^4 - 6 = 3/25 x^2 - 6.
Both sets of parametric equations give us the same curve. However, if we regard t as time, we will find that the point (x, y) moves at different speeds along the two curves. We could easily take the derivatives to find the velocity and speed functions: